class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:##递归终止条件if len(nums) == 1:return TreeNode(nums[0])##找到数组中的最大值以及最大值对应的下标max_value,max_index = self.find_max_list(nums)#根节点是数组中的最大值root_val = max_valueroot = TreeNode(root_val)#根据根节点的位置划分左右子区间, 构造根节点的左右子树#注意index可能为0或者是数组的最后面，导致左右区间为空，如果左右区间为空，那么就没有左或者右子树if max_index >0:left = nums[:max_index]root.left = self.constructMaximumBinaryTree(left)if max_index < len(nums)-1:right = nums[max_index+1:]root.right = self.constructMaximumBinaryTree(right)return rootdef find_max_list(self,nums):#找到数组中的最大值以及最大值对应的下标max_value = 0max_index = 0for i in range(len(nums)):if nums[i] > max_value:max_value  = nums[i] max_index = i return max_value,max_index

617.合并二叉树 

文档讲解：代码随想录

题目链接：. - 力扣（LeetCode）

递归的三要素：

第一要素：明确这个函数想要干什么

传入两个二叉树，返回合并后的二叉树

第二要素：寻找递归结束条件

两棵树是一起遍历的

如果有一个树是空，那么就返回另一个树；如果两个树都是空，那么就return null(这种情况其实已经包含在了前面的条件中)

第三要素：找出函数的等价关系式

从根节点开始，直接去改tree1的结构，不再新定义一棵二叉树了，根节点合并完之后，就要去合并左右子树了，这时候就进入了递归

class Solution:def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:###终止条件if root1 == None:return root2if root2 == None:return root1##单层逻辑递推关系root1.val = root1.val + root2.val#递归root1.left = self.mergeTrees(root1.left,root2.left)root1.right = self.mergeTrees(root1.right,root2.right)return root1

700.二叉搜索树中的搜索 

文档讲解：代码随想录

题目链接：. - 力扣（LeetCode）

递归法

递归的三要素：

第一要素：明确这个函数想要干什么

给定二叉搜索树（BST）的根节点和一个值。在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。

第二要素：寻找递归结束条件

如果根节点的值即为要找的目标值，那么直接return 根节点即可

如果二叉树中只有一个节点，并且根节点的值与目标值不等，那么就返回Null

第三要素：找出函数的等价关系式

如果当前遍历的根节点的值大于目标值，那么接下来就遍历该节点的左子树

如果当前遍历的根节点的值小于目标值，那么接下来就遍历该节点的右子树

class Solution:def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:###递归终止条件if root == None:return Noneif root.val == val:return rootif root.left==None and root.right == None and root.val != val:return None###递归，根据二叉搜索树的特性，选择遍历左子树还是右子树if root.val > val:node = self.searchBST(root.left,val)else:node = self.searchBST(root.right,val)return node

迭代法

从根节点开始查询，根据二叉搜索树的特性，决定向右还是向左搜索

class Solution:def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:while root:if root.val > val:root = root.leftelif root.val < val:root = root.rightelse:return rootif root == None:return None

 98.验证二叉搜索树 

文档讲解：代码随想录

题目链接：. - 力扣（LeetCode）

二叉搜索树的性质：

如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左右子树也为二叉搜索树。

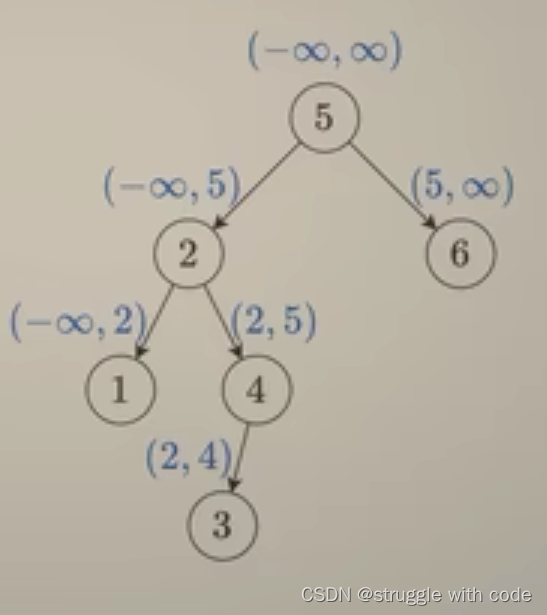
节点的位置越深，节点的值的限制就越多，所以我们可以判断节点是不是满足左右区间的限制，在遍历的过程中，不断去更新左右区间

递归的三要素：

第一要素：明确这个函数想要干什么

传入一个根节点，判断该节点对应的二叉树是否是二叉搜索树

并传入一个区间左端点，一个区间右端点，查看节点值是否满足区间限制，来辅助我们判断

第二要素：寻找递归结束条件

如果传入为空，返回True

如果节点的值不在区间中，那么return false

第三要素：找出函数的等价关系式

如果根节点满足要求，接下来要去看左右子树是否是二叉搜索树，在遍历过程中，如果向左遍历，那么就要更新区间的右端点，如果向右遍历，那么就要更新区间的左端点。

class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:def helper(root,low,upper):###递归终止条件if not root:return Trueif root.val<=low or root.val>=upper: #不要忘记等于的情况return False###递归遍历左右子树left = Trueright = Trueif root.left:left = helper(root.left,low,root.val)if root.right:right =  helper(root.right,root.val,upper)return left and rightreturn  helper(root,float('-inf'),float('inf')) #刚开始根节点的范围是任意的

没有写出来的想法，先不看了

（如果传入节点不是空节点

我们需要递归验证该节点的左子树和右子树是否是二叉搜索树

并且，如果是，那么此时我们还不能确定传入节点是否就是二叉搜索树，因为可能出现这种情况

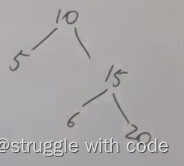
所以我们还需要比较左子树的最大值是否比节点小，右子树的最小值是否比节点大，但是如何去找左子树的最大值和右子树的最小值呢）