文章目录
二叉树
考纲内容
复习提示
1.二叉树的遍历
1.1先序遍历(PreOrder)
1.2中序遍历(InOrder)
1.3后序遍历(PostOrder)
1.4递归算法和非递归算法的转换
1.5层次遍历
1.6由遍历序列构造二叉树
二叉树
考纲内容
(一)树的基本概念
(二)二叉树
二叉树的定义及其主要特征;二叉树的顺序存储结构和链式存储结构;
二叉树的遍历;线索二叉树的基本概念和构造
(三)树、森林
树的存储结构;森林与二叉树的转换;树和森林的遍历
(四)树与二叉树的应用
哈夫曼(Huffman)树和哈夫曼编码;并查集及其应用
复习提示
本章内容多以选择题或综合题的形式考查,但统考也会出涉及树遍历相关的算法题。树和二叉树的性质、遍历操作、转换、存储结构和操作特性等,满二叉树、完全二叉树、线索二叉树、哈夫曼树的定义和性质,都是选择题必然会涉及的内容。
1.二叉树的遍历
二叉树的遍历是指按某条搜索路径访问树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。由于二叉树是一种非线性结构,每个结点都可能有两棵子树,因此需要寻找一种规律,以便使二叉树上的结点能排列在一个线性队列上,进而便于遍历。
【命题追踪——二叉树遍历方式的分析】
【命题追踪——(算法题)二叉树遍历的相关应用】
由二叉树的递归定义可知,遍历一棵二叉树便要决定对根结点 N、左子树L 和右子树R 的访问顺序。按照先遍历左子树再遍历右子树的原则,常见的遍历次序有先序(NLR)、中序(LNR)和后序(LRN)三种遍历算法,其中“序”指的是根结点在何时被访问。
1.1先序遍历(PreOrder)
若二叉树为空,则什么也不做;否则,
1) 访问根结点;
2) 先序遍历左子树;
3) 先序遍历右子树。
图5.7中的虚线表示对该二叉树进行先序遍历的路径,得到先序遍历序列为124635.
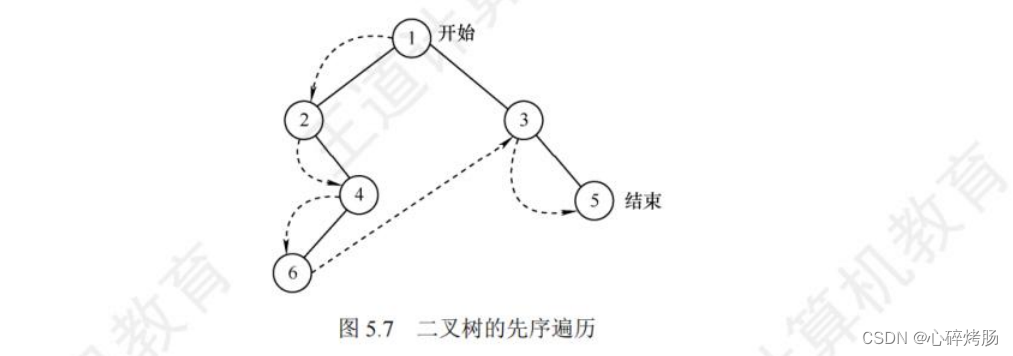
对应的递归算法如下:
void PreOrder(BiTree T){if(T!=NULL){visit(T); //访问根结点PreOrder(T->lchild); //递归遍历左子树PreOrder(T->rchild); //递归遍历右子树}
}
1.2中序遍历(InOrder)
若二叉树为空,则什么也不做;否则,
1) 中序遍历左子树;
2) 访问根结点;
3) 中序遍历右子树。
【命题追踪——中序序列中结点关系的分析】
图5.8中的虚线表示对该二叉树进行中序遍历的路径,得到中序遍历序列为264135。
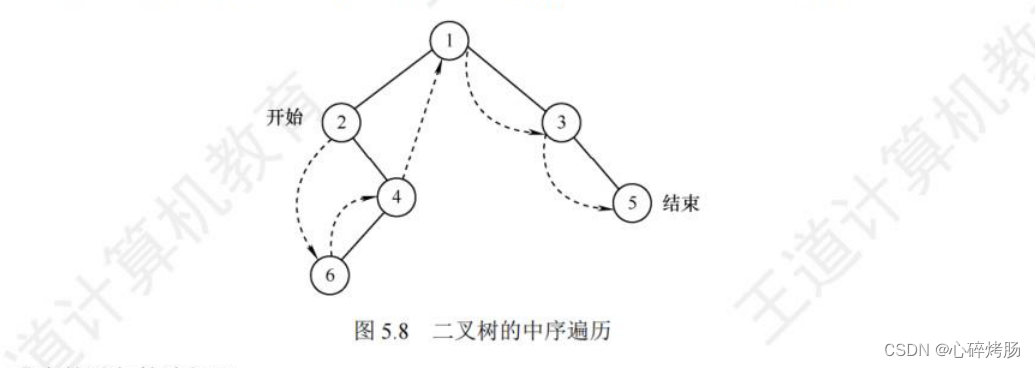
对应的递归算法如下:
void InOrder(BiTree T){if(T!=NULL){InOrder(T->lchild); //递归遍历左子树visit(T); //访问根结点InOrder(T->rchild); //递归遍历右子树}
}1.3后序遍历(PostOrder)
若二叉树为空,则什么也不做;否则,
1) 后序遍历左子树:
2) 后序遍历右子树;
3) 访问根结点。
图 5.9中的虚线表示对该二叉树进行后序遍历的路径,得到后序遍历序列为642531。
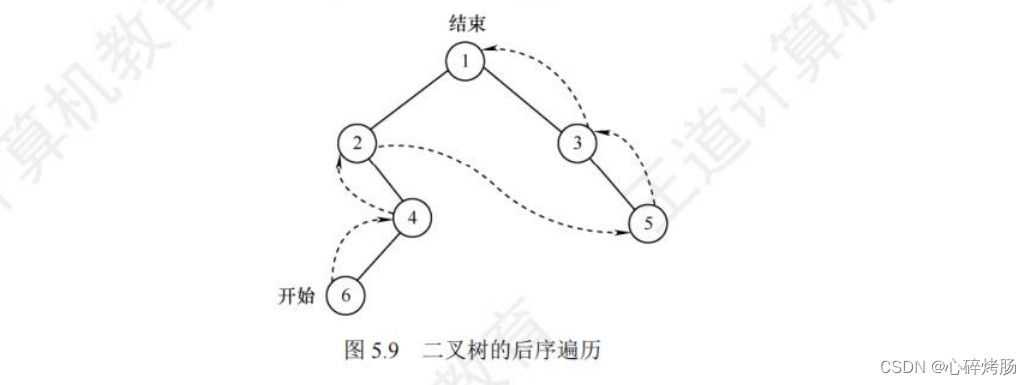
void PostOrder(BiTree T){if(T!=NULL){PostOrder(T->lchild); //递归遍历左子树PostOrder(T->rchild); //递归遍历右子树visit(T); //访问根结点}
}
上述三种遍历算法中,递归遍历左、右子树的顺序都是固定的,只是访问根结点的顺序不同。不管采用哪种遍历算法,每个结点都访问一次且仅访问一次,所以时间复杂度都是 O(n)。
在递归遍历中,递归工作栈的栈深恰好为树的深度,所以在最坏情况下,二叉树是有n个结点且深度为n的单支树,遍历算法的空间复杂度为 O(n)。
1.4递归算法和非递归算法的转换
在上节介绍的三种遍历算法中,暂时抹去和递归无关的 visit()语句,则3个遍历算法完全相同,因此,从递归执行过程的角度看先序、中序和后序遍历也是完全相同的。
注意:非递归遍历算法的难度较大,统考对非递归遍历算法的要求通常不高,
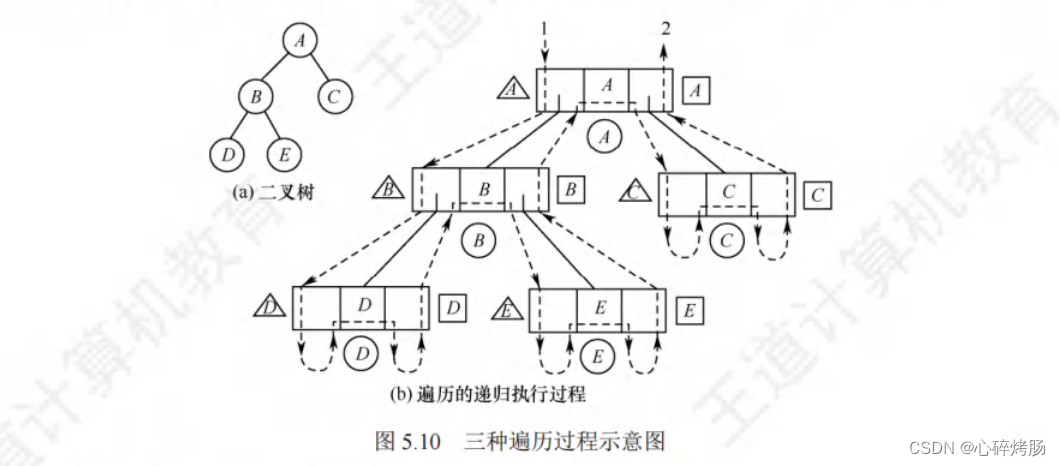
图 5.10 用带箭头的虚线表示了这三种遍历算法的递归执行过程。其中,向下的箭头表示更深一层的递归调用,向上的箭头表示从递归调用退出返回;虚线旁的三角形、圆形和方形内的字符分别表示在先序、中序和后序遍历的过程中访问根结点时输出的信息。
例如,由于中序遍历中访问结点是在遍历左子树之后、遍历右子树之前进行的,则带圆形的字符标在向左递归返回和向右递归调用之间。由此,只要沿虚线从1出发到2结束,将沿途所见的三角形(或圆形或方形)内的字符记下,便得到遍历二叉树的先序(或中序或后序)序列。例如,在图5.10中,沿虚线游走可以分别得到先序序列为 ABDEC、中序序列为 DBEAC、后序序列为 DEBCA。
借助栈的思路,我们来分析中序遍历的访问过程:
①沿着根的左孩子,依次入栈,直到左孩子为空,说明已找到可以输出的结点,此时栈内元素依次为 ABD。
②栈顶元素出栈并访问:若其右孩子为空,继续执行②;若其右孩子不空,将右子树转执行①。
栈顶D出栈并访问,它是中序序列的第一个结点;D右孩子为空,栈顶B出栈并访问;B右孩子不空,将其右孩子E入栈,E左孩子为空,栈顶E出栈并访问;E右孩子为空,栈顶A出栈并访问;A右孩子不空,将其右孩子C入栈,C左孩子为空,栈顶C出栈并访问。由此得到中序序列 DBEAC。
根据分析可以写出中序遍历的非递归算法如下:
void InOrder2 (BiTree T){
InitStack(S);BiTree p=T; //初始化栈 S;p是遍历指针while(p||!IsEmpty(S)){ //栈不空或p不空时循环if(p){ //一路向左Push(S,p); //当前结点入栈p=p->lchild; //左孩子不空,一直向左走}else{ //出栈,并转向出栈结点的右子树Pop(S,p);visit(p); //栈顶元素出栈,访问出栈结点p=p->rchild; //向右子树走,p赋值为当前结点的右孩子} //返回 while 循环继续进入 if-else 语句}
}
先序遍历和中序遍历的基本思想是类似的,只需把访问结点操作放在入栈操作的前面,读者可以参考中序遍历的过程说明自行模拟出入栈示意图。
先序遍历的非递归算法如下:
void PreOrder2 (BiTree T){
InitStack(S); BiTree p=T; //初始化栈 S;p 是遍历指针while(p||!IsEmpty(S)){ //栈不空或p不空时循环if(p){ //一路向左visit(p);Push(S,p); //访问当前结点,并入栈p=p->lchild; //左孩子不空,一直向左走}else{ //出栈,并转向出栈结点的右子树Pop(S,p); //栈顶元素出栈p=p->rchild; //向右子树走,p赋值为当前结点的右孩子} //返回 while 循环继续进入 if-else 语句}
}
后序遍历的非递归实现是三种遍历方法中最难的。因为在后序遍历中,要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点,这就为流程的控制带来了难题。
后序非递归遍历算法的思路分析:从根结点开始,将其入栈,然后沿其左子树一直往下搜索。直到搜索到没有左孩子的结点,但是此时不能出栈并访问,因为若其有右子树,则还需按相同的规则对其右子树进行处理。直至上述操作进行不下去,若栈顶元素想要出栈被访问,要么右子树为空,要么右子树刚被访问完(此时左子树早已访问完),这样就保证了正确的访问顺序。
按后序非递归算法遍历图 5.10(a)中的二叉树,当访问到E时,A,B,D都已入过栈,对于后序非递归遍历,当一个结点的左右子树都被访问后才会出栈,图中D已出栈,此时栈内还有A和 B,这是E的全部祖先。实际上,访问一个结点p时,栈中结点恰好是结点p的所有祖先,从栈底到栈顶结点再加上结点p,刚好构成从根结点到结点p的一条路径。在很多算法设计中都可以利用这一思路来求解,如求根到某结点的路径、求两个结点的最近公共祖先等。
1.5层次遍历
图 5.11 所示为二叉树的层次遍历,即按照箭头所指方向,按照1,2,3,4的层次顺序,自上而下,从左至右,对二叉树中的各个结点进行逐层访问。
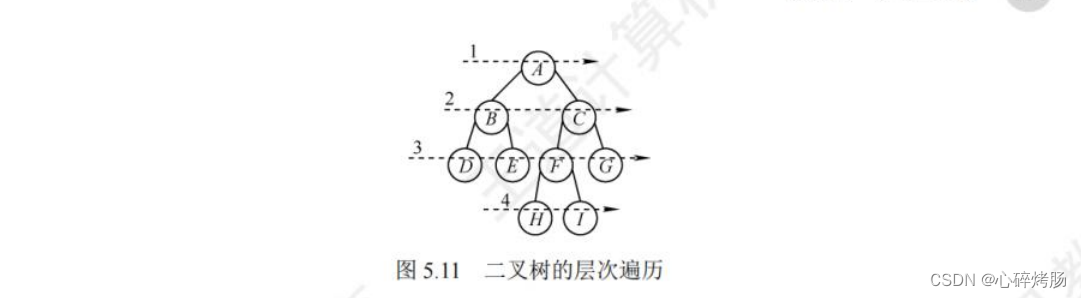
进行层次遍历,需要借助一个队列。层次遍历的思想如下:
①首先将二叉树的根结点入队。
②若队列非空,则队头结点出队,访问该结点,若它有左孩子,则将其左孩子入队;若它有右孩子,则将其右孩子入队。
③重复②步,直至队列为空。
二叉树的层次遍历算法如下:
void LevelOrder(BiTree T){InitQueue(Q); //初始化辅助队列BiTree p;EnQueue(Q T); //将根结点入队while(!IsEmpty(Q)){ //队列不空则循环DeQueue(Q,p); //队头结点出队visit(p); //访问出队结点if(p->lchild!=NULL)EnQueue(Q,p->lchild); //若左孩子不空,则左孩子入队if(p->rchild!=NULL)EnQueue(Q,p->rchild); //若右孩子不空,则右孩子入队}
}
上述二叉树层次遍历的算法,读者在复习过程中应将其作为一个模板,在熟练掌握其执行过程的基础上来记忆,并达到熟练手写的程度。这样才能将该模板应用于各种题目之中。
注意:遍历是二叉树各种操作的基础,例如对于一棵给定二叉树求结点的双亲、求结点的孩子求二叉树的深度、求叶结点个数、判断两棵二叉树是否相同等。所有这些操作都是在遍历的过程中进行的,因此必须掌握二叉树的各种遍历过程,并能灵活运用以解决各种问题。
1.6由遍历序列构造二叉树
【命题追踪——先序序列对应的不同二叉树的分析】
对于一棵给定的二叉树,其先序序列、中序序列、后序序列和层序序列都是确定的。然而,只给出四种遍历序列中的任意一种,却无法唯一地确定一棵二叉树。若已知中序序列,再给出其他三种遍历序列中的任意一种,就可以唯一地确定一棵二叉树。
(1) 由先序序列和中序序列构造二叉树
【命题追踪——先序序列和中序序列相同时确定的二叉树】
【命题追踪——由先序序列和中序序列构造一棵二叉树】
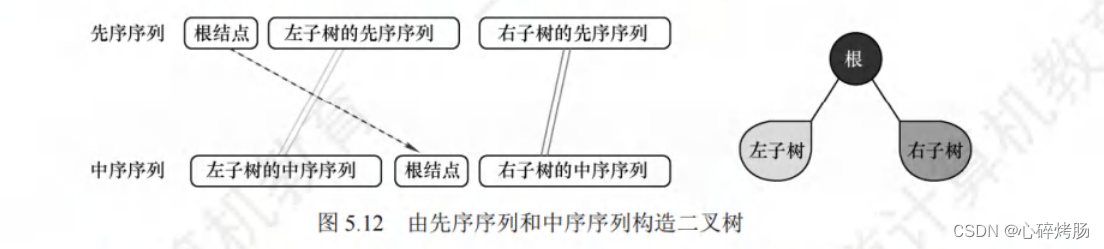
在先序序列中,第一个结点一定是二叉树的根结点;而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列是根的左子树的中序序列,后一个子序列是根的右子树的中序序列。
左子树的中序序列和先序序列的长度是相等的,右子树的中序序列和先序序列的长度是相等的。根据这两个子序列,可以在先序序列中找到左子树的先序序列和右子树的先序序列,如图 5.12 所示。如此递归地分解下去,便能唯一地确定这棵二叉树。
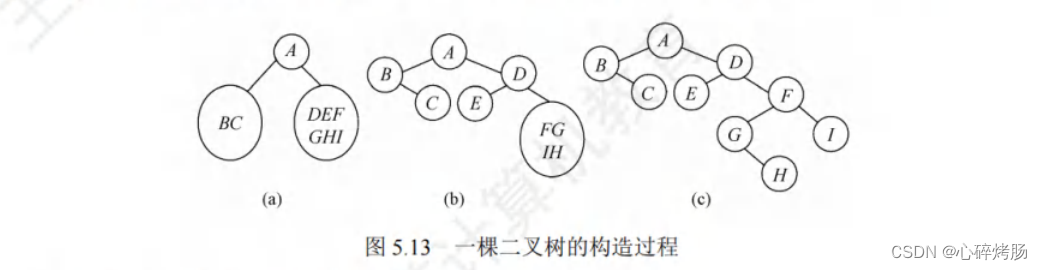
例如,求先序序列(ABCDEFGHI)和中序序列(BCAEDGHFI)所确定的二叉树。
首先,由先序序列可知A为二叉树的根结点。中序序列中A之前的 BC为左子树的中序序列,EDGHFI为右子树的中序序列。
然后,由先序序列可知B是左子树的根结点,D是右子树的根结点。
以此类推,就能将剩下的结点继续分解下去,最后得到的二叉树如图5.13(c)所示。
(2) 由后序序列和中序序列构造二叉树
【命题追踪——由后序序列和树形构造一棵二叉树】
同理,由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树。因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,如图5.14 所示,然后采用类似的方法递归地进行分解,进而唯一地确定这棵二叉树。
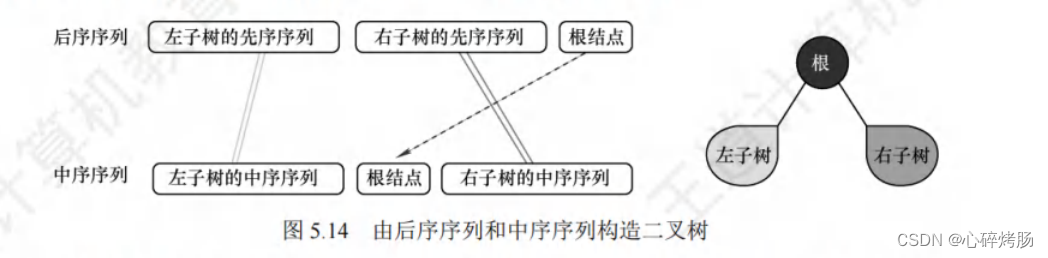
请读者分析后序序列(CBEHGIFDA)和中序序列(BCAEDGHFI)所确定的二叉树。
(3) 由层序序列和中序序列构造二叉树
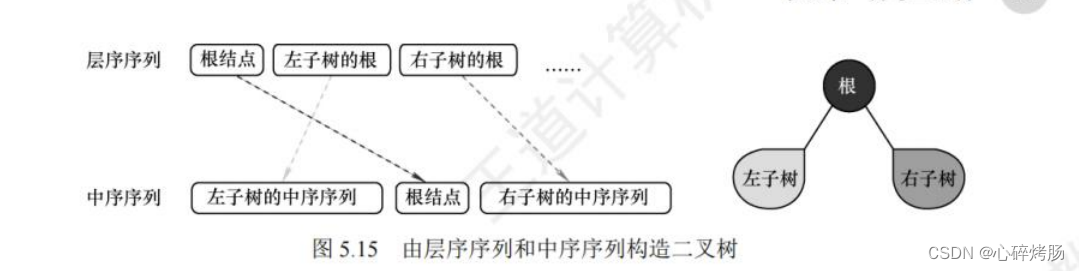
在层序遍历中,第一个结点一定是二叉树的根结点,这样就将中序序列分割成了左子树的中序序列和右子树的中序序列。
若存在左子树,则层序序列的第二个结点一定是左子树的根,可进一步划分左子树;
若存在右子树,则中序序列中紧接着的下一个结点一定是右子树的根,可进一步划分右子树;
如图5.15 所示。采用这种方法继续分解,就能唯一确定这棵二叉树。
请读者分析后序序列(ABDCEFGIH)和中序序列(BCAEDGHFI)所确定的二叉树。
需要注意的是,先序序列、后序序列和层序序列的两两组合,无法唯一确定一棵二叉树。
例如,图 5.16所示的两棵二叉树的先序序列都为 AB,后序序列都为 BA,层序序列都为 AB。