本文重点
在数学领域中,极值是一个极其重要的概念,它不仅在纯数学理论研究中占据核心地位,而且在工程、物理、经济等实际应用领域也发挥着不可替代的作用。极值问题涉及函数的最大值和最小值,是微积分学中的一个基本问题。本文旨在详细介绍数学中的极值概念、性质、求解方法以及其在各个领域的应用。
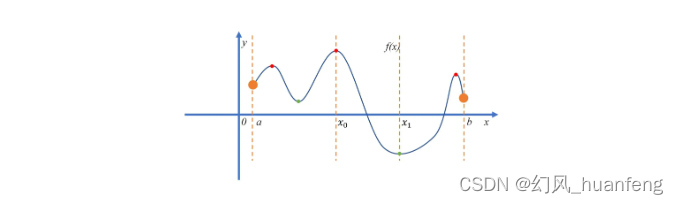
极值的定义与性质
极值的定义
极值是指函数在某一区间内,当自变量取某一特定值时,函数值达到最大或最小。具体来说,如果函数f(x)在x=c处的函数值大于或等于其邻近的所有值,则称f(c)是函数f(x)的局部最大值;如果函数f(x)在x=c处的函数值小于或等于其邻近的所有值,则称f(c)是函数f(x)的局部最小值。如果在整个定义域内,f(c)都是最大的或最小的,则称f(c)是函数f(x)的全局最大值或全局最小值。
极值的性质
极值具有以下基本性质:
(1)极值点处的一阶导数等于零(或不存在)。这是因为如果函数在某点处可导且取得极值,则该点处的一阶导数必须为零。然而,一阶导数等于零的点并不一定是极值点,也可能是拐点或其他类型的点。
(2)极值点处的二阶导数可以用来判断极值的类型。如果函数在某点处二阶导数大于零,则该点是局部最小值;如果二阶导数小于零,则该点是局部最大值。这一性质在求解极值问题时非常有用。