点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

二分查找算法简单介绍
关于二分查找原理我们干巴巴的说也没有意思，我们在具体题目中在一一介绍，这里我们主要想说的是二分查找算法的特点，以及它的侧重点！

1. 特点

最恶心，细节最多，最容易写出死循环的算法。如果掌握了它就会变成最简单的塞凡。

2. 侧重点

算法原理：以前我们可能就听过这样一句话，二分查找适合数组有序的情况，但是当真正理解它算法原理之后，二分查找其实一个非常牛逼的算法，不仅适合数组有序的情况，即使数组无序的情况，只要发现数组中规律能够使用二分查找，就使用二分查找，管它是有序还是无序。

模板：高度抽象化之后固定得格式。但是不要死记硬背！一定要理解之后再记忆！
朴素的二分模板 ----> (简单但有局限)
查找左边界的二分模板、查找右边界的二分模板 ---->（万能但细节多）
后面在题中在总结

1. 二分查找

题目链接：704. 二分查找

题目分析：

这道题非常重要的就是数组有序！

算法原理：

数组从左往右走一一排除。
解法一：暴力求解
时间复杂度O(N)

我们看也没有优化的可能，暴力解法没有利用数组有序的条件。假设数组中我们随便拿一个数4，目标数是target，因为是数组是升序的，我们发现4的左边区间的数比我这个4小，并且4本身还比target小的。那么这个区间都是比target小的，那根本就不可能能等于5，因此这块区间就可以直接干掉，然后从右边区间找就可以了。我们仅仅比较一次就干掉一批数，所以说用这个规律绝对比暴力求解强！

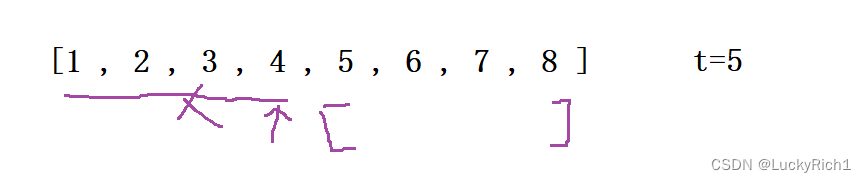
假设现在又找到数7比5大，7已经比5大了，它后面铁定比5大，因为后面数比7还大，因此我们可以把7包含7后面的区间干掉，然后再新的区间找。

我们总结这个规律：在一个数组中随便找一个点，发现这个数和target做比较后，划分成两个区域，其中根据规律我们可以有选择性舍去一个区域，然后在另一个区域寻找。此时我们称这个题里面是有二段性的，如果有二段性，我们就可以使用二分查找算法解决这个问题

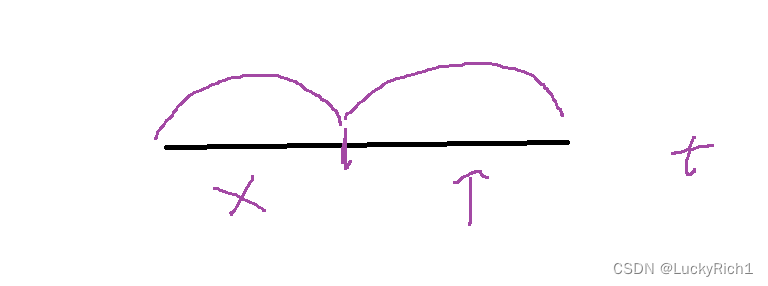
解法二：二分查找算法
本道题有二段性就可以用二分查找算法，这是非常重要的，而不是像别人说的数组有序才能用二分查找。二分查找的本质是当数组有二段性就可以用二分查找算法。 ，数组无序但是发现有二段性也可以用二分查找！

二段性：当我们发现一个规律，根据这个规律选取某一个点，能把数组分成两部分，然后根据规律有选择性的舍去一部分，在另一部分查找。此时就可以用二分查找算法

这个点怎么选呢？建议就选中间的节点，根据数学概率学，选1/2直接干掉一半

定义两个指针left，right刚开始指向左端点和右端点，找到一个mid点，利用上面性质根据这个点来确定寻找区间，然后就有三种关系：

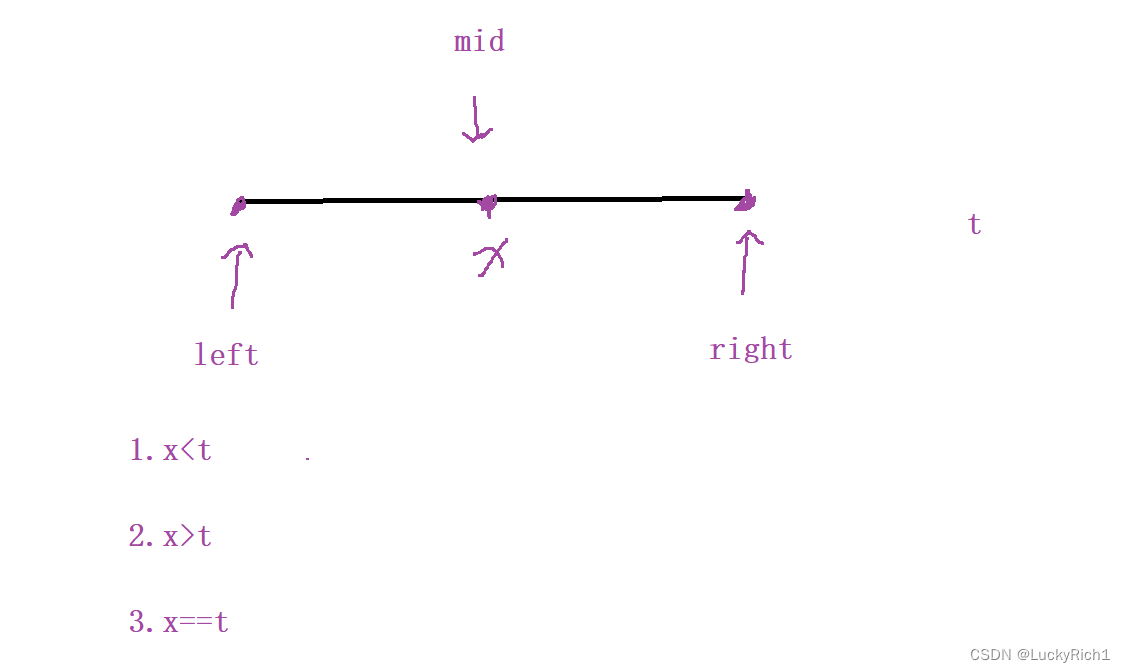
1. x<t，根据规律把左边区间删掉 left=mid+1 ，从新的【left，right】寻找
2. x>t，根据规律把右边区间删掉 right=mid-1，从新的【left，right】寻找
3. x==t，返回结果

以上就是朴素二分查找算法的核心步骤

不过还有一些细节问题：

1. 循环结束的条件

当left>right循环结束，当left<=right循环继续

2. 为什么是正确的

虽然仅比较一次就去掉一部分区间，但是我们做到暴力解法比较多次才能去掉这段区间。所以是和暴力解法一样正确的

3. 时间复杂度

时间复杂度一般是最坏情况下的执行次数，

class Solution {
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){//int mid=(left+right)/2 有溢出的风险int mid=left+(right-left)/2;//防止溢出if(nums[mid]<target)left=mid+1;else if(nums[mid]>target)right=mid-1;elsereturn mid;}return -1;}
};

总结朴素二分模板：
根据题目要求往里面填内容，具体根据那道题分析出来的二段性来填

while(left<=right)
{int mid=left+(right-left)/2;if(...)left=mid+1;else if(...)right=mid-1;elsereturn ...;
}

细节一：一定是left<=right
细节二：找中间点防溢出的方式，left+(right-left)/2， 其实找中间点有两种写法，+1和不+1:
普通+1：(left+right+1)/2
防溢出+1：left+(right-left+1)/2
不过对于数组个数为奇数求中间点的时候，+1，不+1是没有区别的都是指向同一个点。个数是偶数求中间点的时候，中间点是有两个数的，不+1在左边，+1在右边。

不过对于朴素版本来说都是无所谓的 ！+1不+1都可以。因为在朴素这里仅需找到一个点就可以，然后根据这个点来划分左右区间就可以，这个点在中间点那个位置我并不关心！

2.在排序数组中查找元素的第一个和最后一个位置

题目链接： 在排序数组中查找元素的第一个和最后一个位置

题目分析:

一个非递减的排序的数组的意思就是递增或者不变的数组。

算法原理：

解法一：暴力求解

这道题很容易就会想的到暴力求解，从前向后遍历，标记出现target的第一个位置和最后一个位置。但是时间复杂度是O(N)

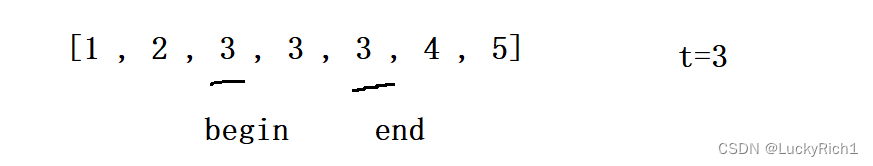
因为这也是一个有序数组，所以还可以想到二分查找，我们用刚学的朴素二分查找算法试一下，但是虽然你找到这个位置，但这并不是答案，你还要从这个位置，往左找第一个出现的位置，往右找第一个出现的问题，极端条件下整个数组都是target，那时间复杂度就退化到O(N)了。

我们需要想到一个更优秀的策略，依旧是二分，依旧要用到数组有序的情况。只不过是在朴素二分的基础上对二分策略做一下优化！

回到二分的本质，当我们发现这道题有个规律 “二段性”，我们就可以利用二分查找。
因为我们要找第一个和最后一个，不能同时寻找，所以我们分开考虑，先找第一个。

1.查找区间的左端点

以下面例子为例，当我们找到最左端点时，把数组划分两部分。左区域小于t，右区域大于等于t。因此我根据target在查找区间左端时，发现数组是具有二段性的就可以用二分

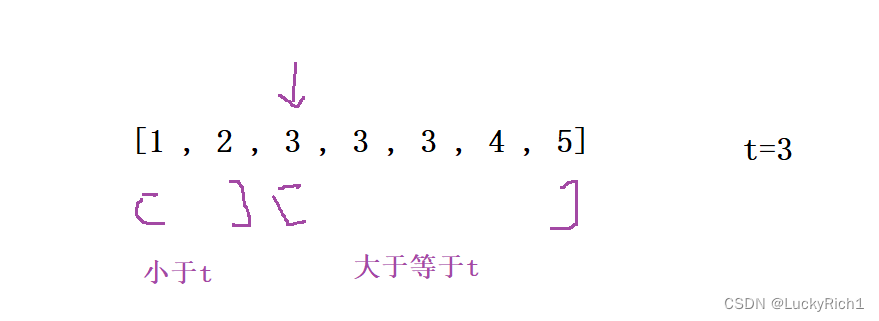
定义两个指针，找左端点。具体操作如下

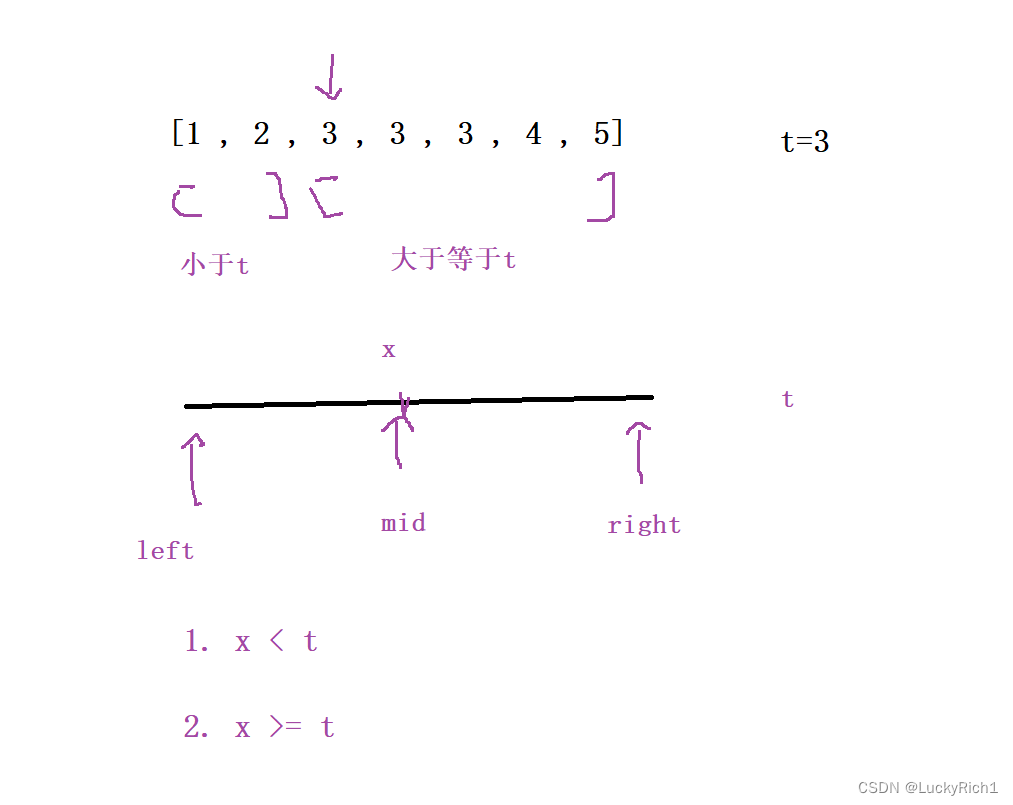
1. x < t ，也就是说mid此时所在区间是小于t的，因此 left=mid+1，然后再新的【left，right】找
2. x >= t，为什么把大于等于放一块，因为你这次找的值虽然和target相同，但可能并不是最左端点，可能是最左端点的右边。或者就是值比target大的点，这两种处理方法是一样的。那此时right=mid-1吗？并不是，如果万一 这个点就是最左端点，right=mid-1，那不就走过去了，因此 right=mid， 然后再新的【left，right】找

这两句是整个代码的核心，但是难点并不在这里。最恶心，最容易出错地方在细节哪里。

细节处理：

细节一：循环条件

一种循环条件 left<=right，另一种是left<right ，选那个？
选left<right作为循环条件
原因如下，这数组一共就三种情况；
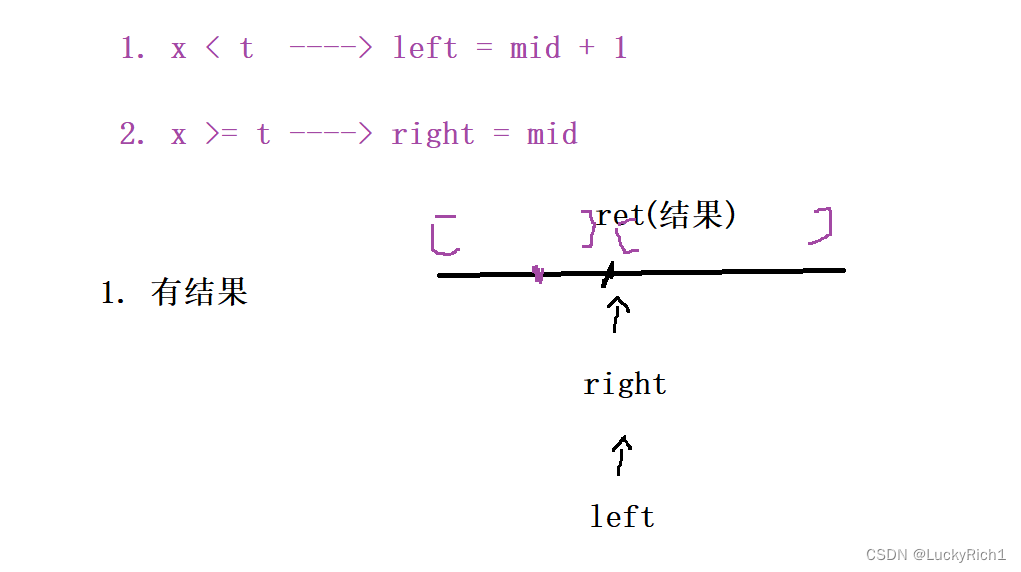
1.有结果
刚开始left处于不合法区间，right处于合法区间，left一直在不合法的区间移动，right一直在合法区间移动。而且会发现right在合法区间移动不会超过ret，因为right=mid。left一直在想跳出这个不合法区间，因为left=mid+1。当left和right相遇的位置恰好就是left跳出不合法区间的位置。所以说当left和right相遇的位置正好是最终结果

所以，当left = right 的时候，就是最终结果，无需在进循环判断

2.全大于t
只会命中x>=t，也只有right一直在移动，直到left和right相遇为止，但是没有最终结果，仅需判断这个相遇位置的值是否等于target，相等返回下标不等返回-1，也就是
当left = right 的时候，就是最终结果，无需在进循环判断。

3.全小于t
只会命中x<t，left一直向右移动，直到遇到right，当left和right相遇，也是仅需判断是否和target相遇，没必要在循环了。

所以，以上三种情况都是符合：当left = right 的时候，就是最终结果，无需在进循环判断 这是第一点。

第二点，如果判断了，就会死循环

当两个指针都指向ret的时候，如果继续判断你会发现mid依旧还是指向这个值，命中第二个条件，right并不会移动！ 就死循环下去了！

细节二：求中点操作

求中断我们用防溢出的，无非就是两种选择。
left + ( right - left ) / 2
left + ( right - left + 1 ) / 2

前面说过如果个数是奇数选+1/不+1没有区别，指向的同一个位置。如果数组个数是偶数是，用第一种方法是求得靠左的位置，用第二种方法求得是靠右得位置。这两种方法在朴素二分哪里没有问题。但是在这里就不行了！

假设我们选left + ( right - left + 1 ) / 2求中点，当最后一次操作就剩下两个数了，mid落在right这里，如果命中第一个条件，left=mid+1此时没问题循环，但是如果命中第二个条件，right=mid，你会发现mid根本没动，下一次还是它，在下一次还是它，就会死循环！

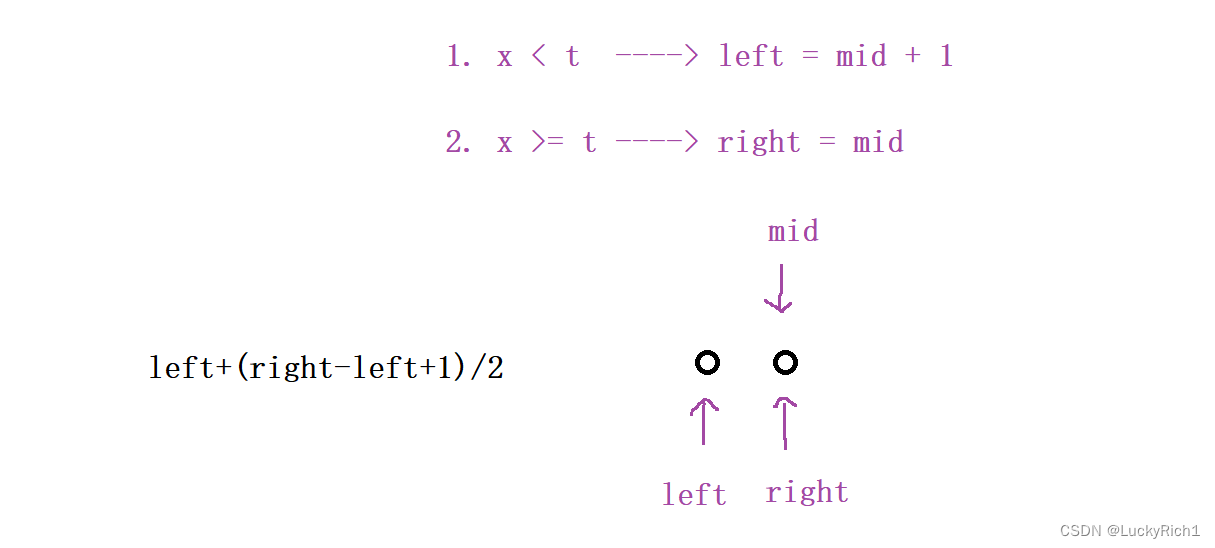
假设我们选left + ( right - left ) / 2求中点，最后一次操作就是想两个数，mid落在left这里，命中x<t，那left和right相遇就会跳出循环，命中x>=t，left和right也还会相遇也还是跳出循环。

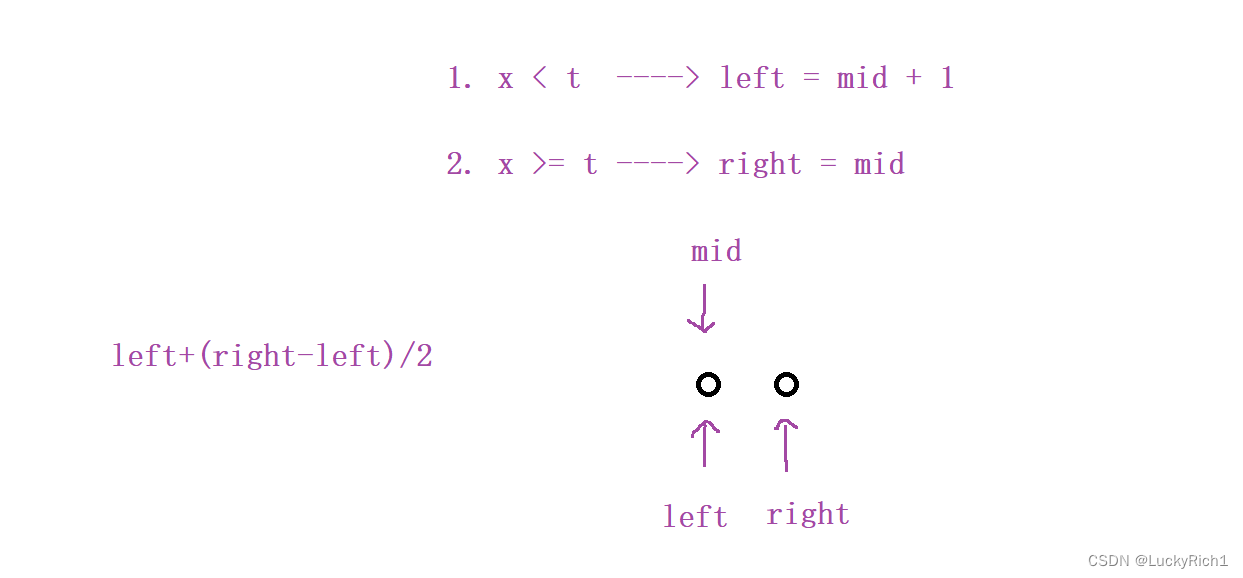
所以求中点操作left + ( right - left ) / 2

当这两个细节问题处理完了，我们查找区间的左端点就完成了。

总结查找区间的左端点的核心：

1. x < t， left=mid+1，然后再新的【left，right】找
2. x >= t，right=mid， 然后再新的【left，right】找

循环条件：left < right
求中点操作：left + ( right - left ) / 2

2.查找区间右端点
其实查找区间右端点思路和查找区间左端点思路是一样的，但是细节不一样。
根据右端点依旧可以把数据划分成两部分，左边小于等于target，右边大于target。
根据这个二段性，我们就可以使用二分。

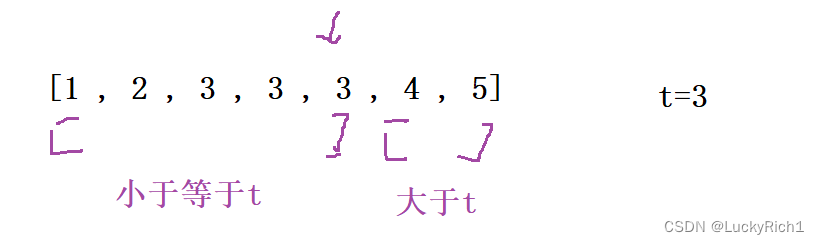
定义两个指针，找到mid，根据这个x分情况讨论

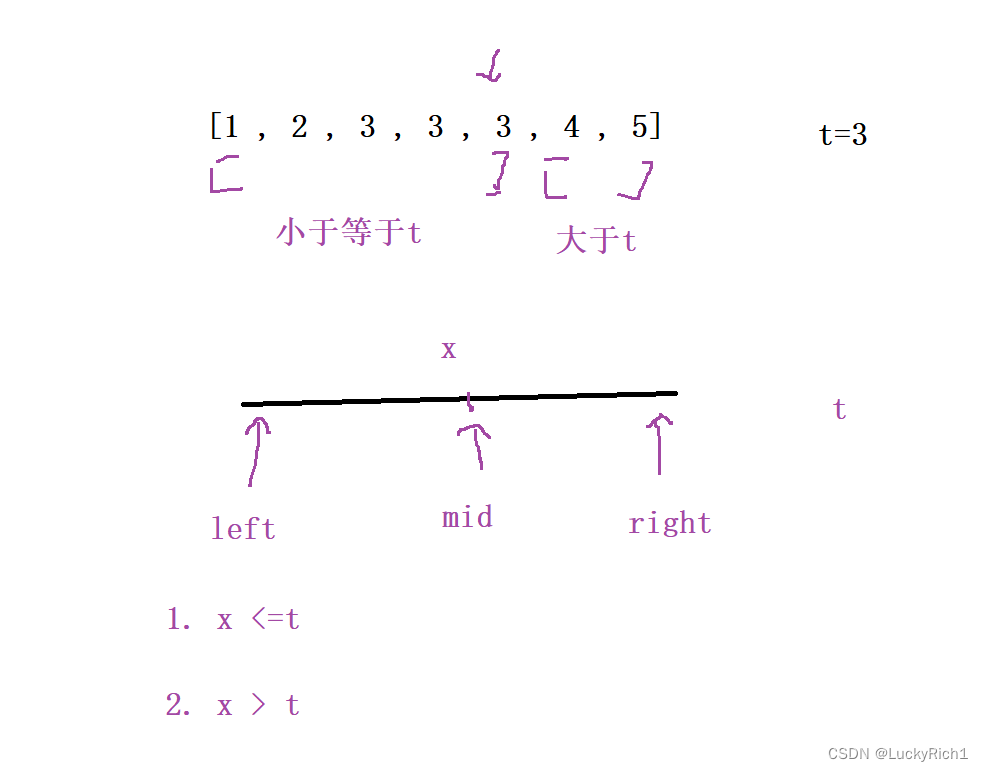
1. x <= t ，mid落在左边区域，同理left不能越过mid，因为mid可能就是指向了最终结果，如果指向最终结果，left=mid+1了，那接下里查找区间就没有最终结果了。left=mid，然后再新的【left，right】找
2. x > t，mid落在右边区域，因为mid落在的区间一定大于target不符合要求，所以right=mid-1，然后再新的【left，right】找

重点依旧是处理细节问题：

细节处理：

细节一：循环条件

原因同上面一样 left < right，

细节二：求中点操作

left + ( right - left ) / 2
left + ( right - left + 1 ) / 2

假设选的是left + ( right - left ) / 2，当最后一次操作就剩下两个数了，mid此时在left这里，如果命中x>t，right=mid-1跳出循环，如果命中x<=t，left=mid，mid经过计算还是老位置根本不动，最终会导致死循环

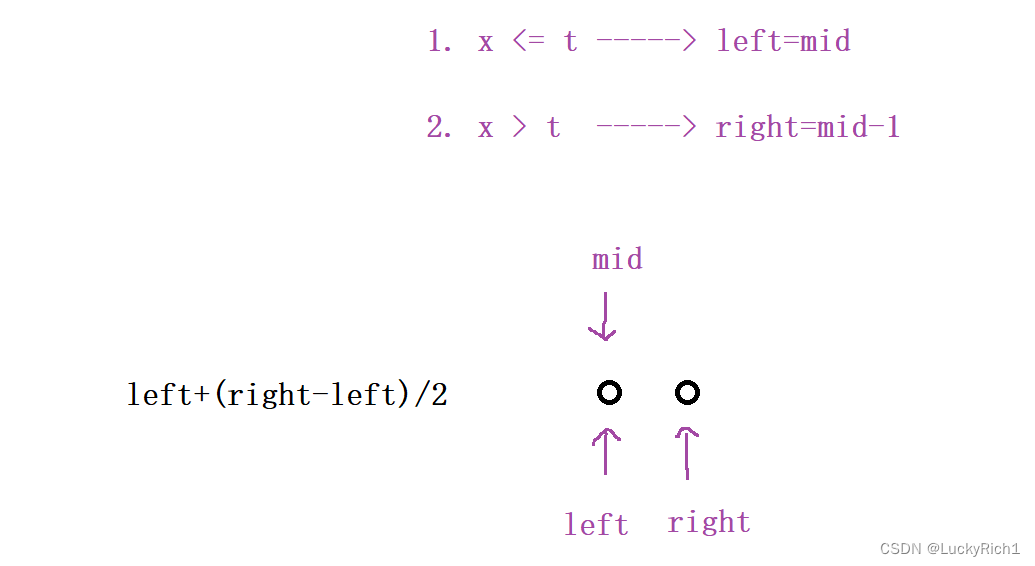
假设选的是left + ( right - left ) / 2，当最后一次操作就剩下两个数了，mid此时在right这里，如果命中x>t，right=mid-1，那left和right相遇就会跳出循环，如果命中x<=t，left=mid，那left和right还是相遇也会跳出循环

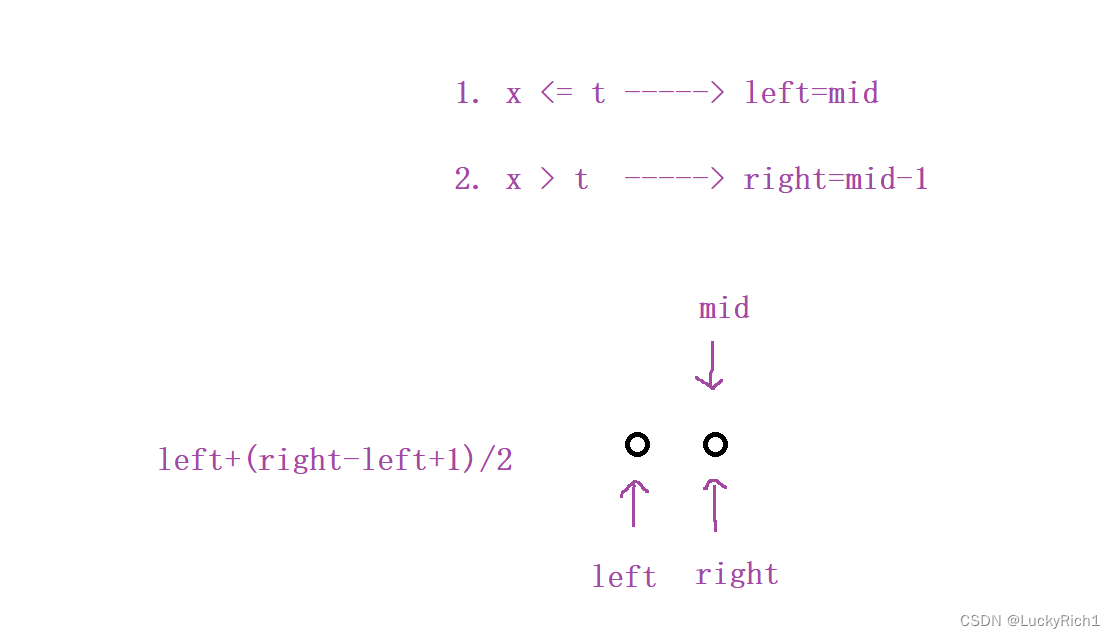
因此求中点操作left + ( right - left + 1) / 2

总结查找区间的右端点的核心：

1. x <= t， left=mid，然后再新的【left，right】找
2. x > t，right=mid-1， 然后再新的【left，right】找

循环条件：left < right
求中点操作：left + ( right - left + 1 ) / 2

原理我们都清楚了，我们就可以写代码了：

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.empty()) return{-1,-1};int begin=0;int left=0,right=nums.size()-1;//1. 二分左端点while(left<right){int mid=left+(right-left)/2;if(nums[mid] < target) left=mid+1;else right=mid;}//判断是否右结果if(nums[left] != target) return {-1,-1};begin=left;// 2.二分右端点left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid] <= target) left=mid;else right=mid-1;}return {begin,right};}
};

总结：查找左边界的二分模板、查找右边界的二分模板

除了判断条件一样，其余的都不一样，如果要是死记硬背肯定有差错，一定要理解记忆。

其实我们仅需记住求中点操作就可以了， 下面两句我们画图很容易推出来。无非就是细节问题很恶心。

上面判断都是left<right我们不用记忆，仅需要记住求中点操作，求左端点不加1，求右端点要+1。还可以这样记，当下面出现 -1 的时候，上面就 +1，具体left、right怎么办就分类讨论，就题论题即可！

3.x 的平方根

题目链接：69. x 的平方根

题目分析：

这道题让找算术平方根，我们可以换个思路找谁的平方根是x

算法原理：

解法一：暴力求解
遍历直到找到一个数的平方大于或者等于x。
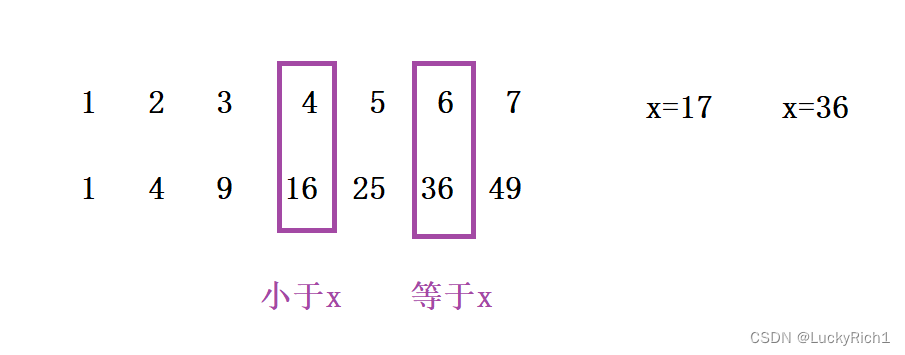
比如说x=17，当遍历到5的平方25的时候，大于x，但是4的平方16小于x，因此是一个4.xxx的数，题目只需要保留整数部分，因此最终结果是4

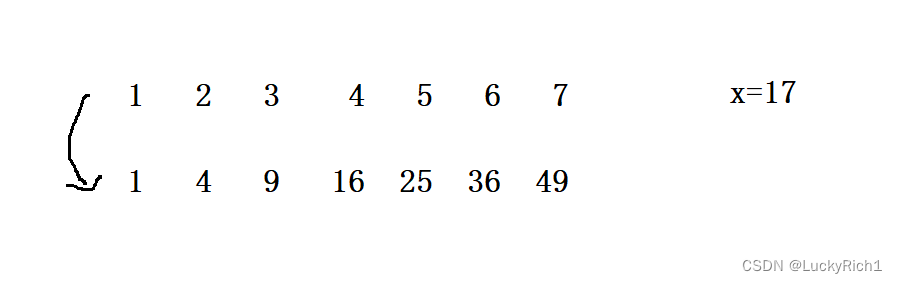
我们发现这是一个有序的，我们看看能不能发现二段性，进而将暴力解法改成二分查找。 我们就盯着结果来，发现结果要么小于x要么等于x。

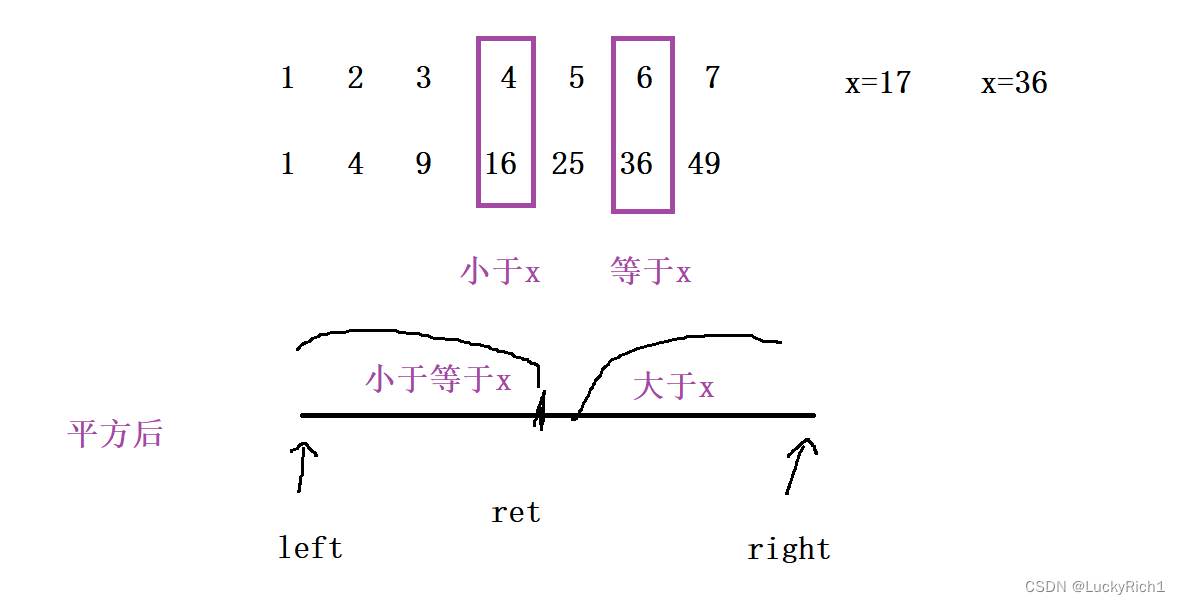
因此我们就发现了二段性，最终结果将整个区间分成两个区间，左边区间小于等于x，右边区间大于x。

解法二：二分查找

目前我们学了三种二分查找，朴素、查找区间左端点、查找区间右端点三种二分查找算法。我们以后遇到的上档次题几乎不会用到朴素二分查找！ 因此用不朴素的的！

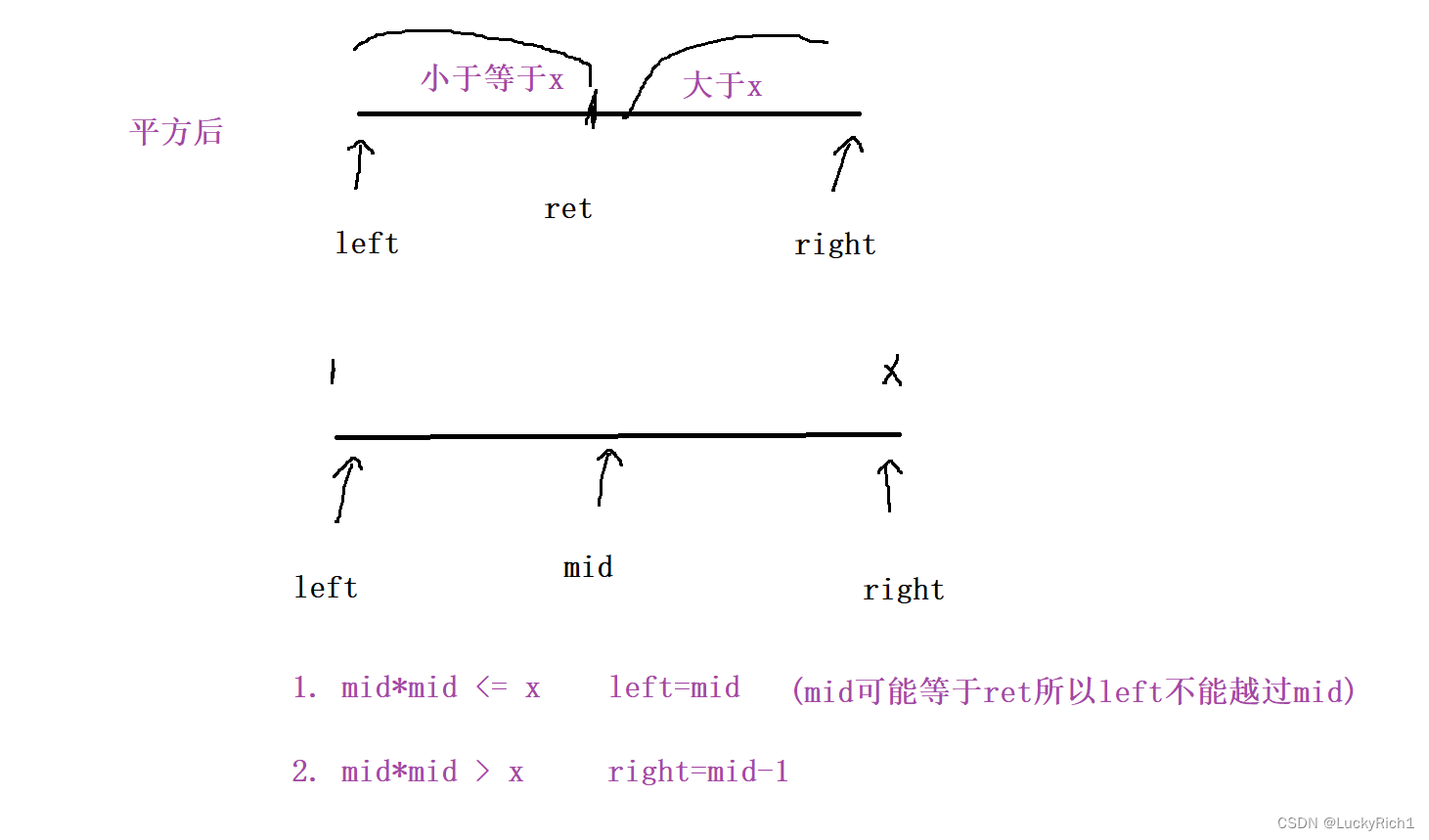
下面就是具体分析过程

class Solution {
public:int mySqrt(int x) {if(x < 1) return 0;int left=1,right=x;while(left < right){long long mid=left+( right - left + 1 )/2;if(mid*mid<=x) left=mid;else right=mid-1;}return left;}
};

4.搜索插入位置

题目链接：35. 搜索插入位置

题目分析：

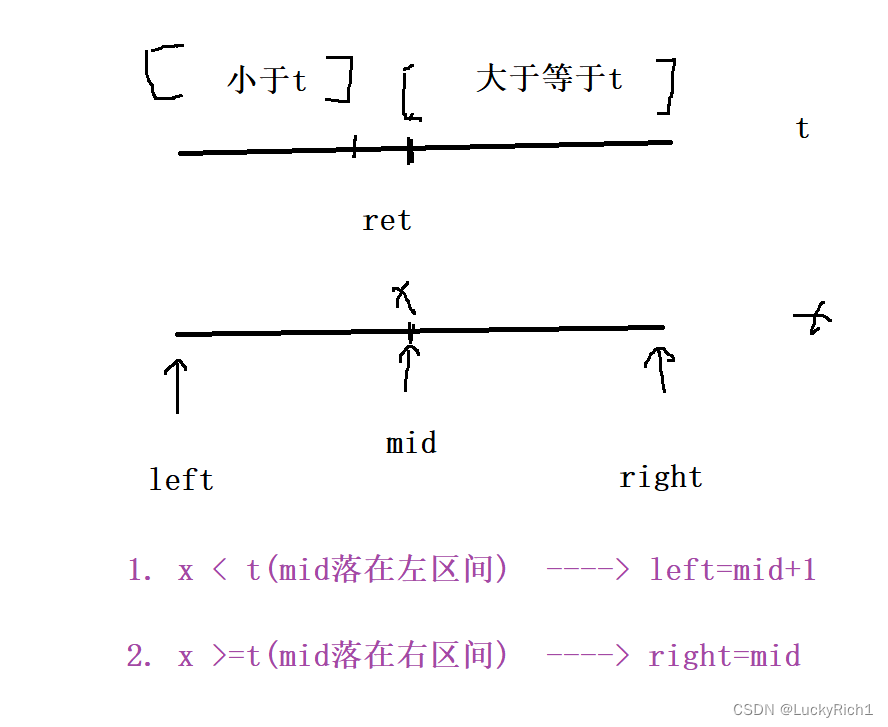
根据题目意思就是要使用二分查找，我们先看看有没有二段性。根据题目要求数组有该值就返回该值的下标，没有就插入返回插入的下标，我们发现插入的下标是第一个大于它的数的位置。由此我们就发现了二段性，ret要么是本来就有该值的位置或者是插入的位置。ret将整个数组分为两部分，左区间小于t，右边大于t

算法原理：二分查找

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}if(nums[left]<target) return left+1;return left;}
};