上学
题目描述
usst 小学里有 n 名学生,他们分别居住在 n 个地点,第 i 名学生居住在第 i 个地点,这些地点由 n−1 条双向道路连接,保证任意两个地点之间可以通过若干条双向道路抵达。学校则位于另外的第 0 个地点,第 0 个地点与第 1 个地点之间有另外一条双向道路链接。
最近学校开始启用校车来接学生上学,每一辆校车上都可以坐无限个学生,且每辆校车在一天内不会重复经过一条道路,校车终点始终为学校。每一位学生一天内只能乘坐一辆校车,且只能在自己居住的节点处上车,在学校下车。为了节省资金,学校会在保证每位学生都能坐上校车的前提下,安排最少数量的校车,每天早上从某些地点出发,并经过若干道路和地点最终抵达学校。第 x 位学生可以自由选择一辆经过第 x 个地点的校车,搭乘它到达学校。
现在学校想要从 n 个学生中选出 3 人参加某个比赛,但是学校不希望这 3 人之间太过 “熟悉”,请问一共有多少种不同的选人方案。
如果一种选择方案中, 3 个人可能在同一天里乘坐上同一辆校车,那就称这 3 个人之间太过 “熟悉”。
对于任意两个方案,如果存在一名学生在一个方案中且不在另一个方案中,那么就认为这两种方案不同。
输入描述
输入第 1 行包含 1 个正整数 n ,代表学生数量和学生居住的地点数量。( 3 ≤ n ≤ 2 × 1 0 5 3≤n≤2×10^5 3≤n≤2×105)
接下来 n−1 行每行有 2 个正整数 u, v ,代表第 u 个地点与第 v 个地点之间有一条双向道路。( 1 ≤ u , v ≤ n 1≤u,v≤n 1≤u,v≤n)
输出描述
输出一行,一个整数,代表选人方案数量。
样例输入 #1
5
1 2
2 3
3 4
4 5
样例输出 #1
0
样例输入 #2
5
1 2
2 3
2 4
1 5
样例输出 #2
8
原题
牛客——传送门
思路
根据题目描述可知,学校所选择的校车的路线是每个由叶子节点指向根节点(即节点1)的路径。题目目的是求出从 n 个学生中选择 3 个学生,保证 3 个学生不在同一条由叶子节点指向根节点(即节点1)的路径中的方案数。那么可以采用容斥原理,用不考虑 3 个学生在一条路径上的总的方案数减去 3 个学生在一条路径上的方案数。
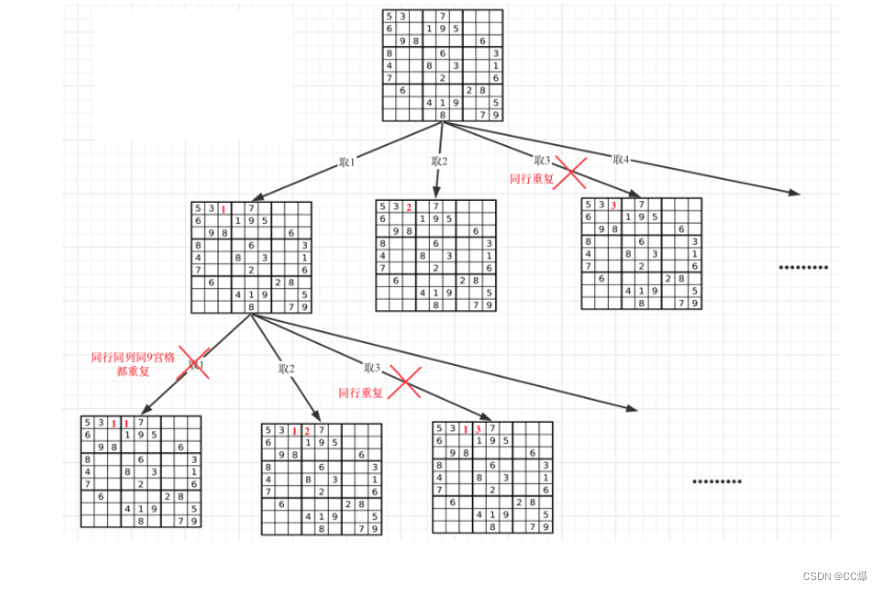
求解示例如下:
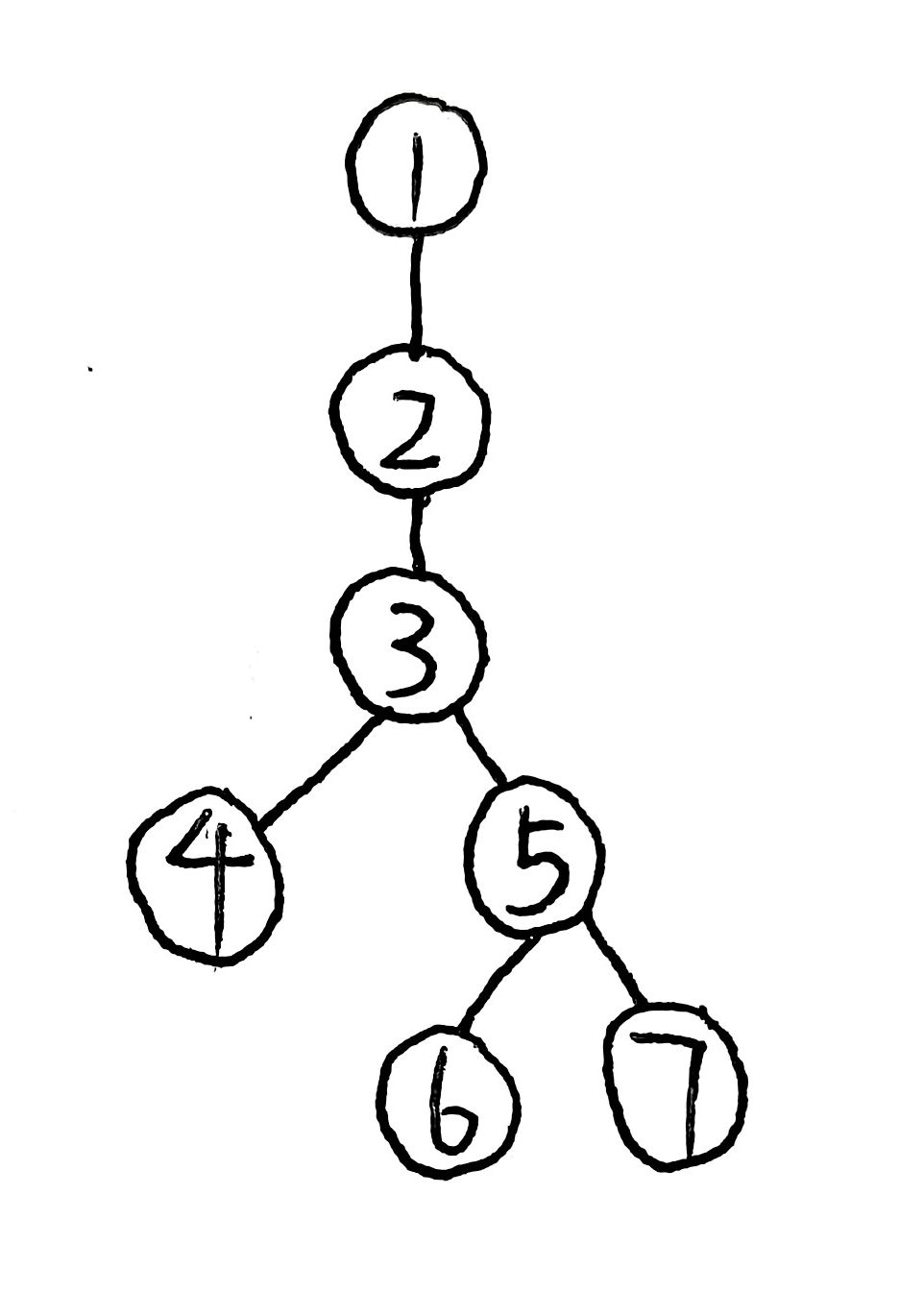
对于上图所示的树,存在三条从叶子节点到根节点的路径,即 4-1,6-1,7-1,也就是三辆校车行驶的路线。首先,总的方案数为C(n,3)。而 3 个学生在一条路径上的方案数求解如下:C(4,3)+C(5,3)+C(5,3)-C(4,3)-C(3,3)。意思是4-1,6-1,7-1的三条路径中各自分别选取 3 个学生,但是存在重复选取5-1路径和3-1路径的情况。所以我们需要去重,即因为 5 节点下面有两条支链,所以要减去5-1路径的方案数乘以2-1(因为有两条支链,重复求了一次,所以2-1表示多求的数量)即减去C(4,3)。同理,还需要减去3-1路径的方案数即C(3,3)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int maxn = 2e5 + 6;
vector<int> e[maxn]; // 邻接表存边
vector<pair<int, int>> num; // num.first为路径上的节点个数,num.second为该路径需要计算多少次void dfs(int p, int fa, int depth)
{if (p != 1 && e[p].size() <= 1) // 找到叶子节点{if (depth >= 3){num.push_back({depth, 1});}return;}int child_num = 0; // 支链数量,即孩子数量for (int i = 0; i < e[p].size(); i++) // 树的递归遍历{int v = e[p][i];if (v != fa){dfs(v, p, depth + 1);child_num++;}}if (depth >= 3) // 去重{num.push_back({-depth, child_num - 1}); // 加入num数组数指定为-depth,为的是做个标记}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);ll n;cin >> n;for (int i = 1; i < n; i++){int u, v;cin >> u >> v;// 存无向边e[u].push_back(v);e[v].push_back(u);}dfs(1, 0, 1);// 先计算总方案数C(n,3)ll ans = n * (n - 1) * (n - 2) / 6;for (int i = 0; i < num.size(); i++){ll x = num[i].first;if (x > 0) // 若为正数,表示这是叶子节点到根节点的路径中选取学生的方案数ans -= x * (x - 1) * (x - 2) / 6;else // 标记为负数,表示这是要去重的路径中选取学生的方案数{x = -x;ans += x * (x - 1) * (x - 2) / 6 * (ll)num[i].second;}}cout << ans;return 0;
}