python之二维几何学习笔记

一、概要

资料来源《机械工程师Python编程：入门、实战与进阶》安琪儿·索拉·奥尔巴塞塔 2024年6月

点和向量：向量的缩放、范数、点乘、叉乘、旋转、平行、垂直、夹角
直线和线段：线段中点、离线段最近的点、线段的交点、直线交点、线段的垂直平分线
多边形：一般多边形、圆、矩形
仿射变换

书中强调了单元测试的重要性。

二、点和向量

数字比较

# geom2d/nums.pyimport mathdef are_close_enough(a,b,tolerance=1e-10):return math.fabs(a-b)<tolerancedef is_close_to_zero(a,tolerance=1e-10):return are_close_enough(a,0.0,tolerance)def is_close_to_one(a,tolerance=1e-10):return are_close_enough(a,1.0,tolerance)

点

# geom2d/point.pyimport mathfrom geom2d import nums
from geom2d.vector import Vectorclass Point:def __init__(self, x, y):self.x = xself.y = y# 计算两点间的距离def distance_to(self, other):delta_x = other.x - self.xdelta_y = other.y - self.yreturn math.sqrt(delta_x ** 2 + delta_y ** 2)# 对点进行加操作def __add__(self, other):return Point(self.x + other.x,self.y + other.y)# 对点进行减操作def __sub__(self, other):return Vector(self.x - other.x,self.y - other.y)# 用向量移动点def displaced(self, vector: Vector, times=1):scaled_vec = vector.scaled_by(times)return Point(self.x + scaled_vec.u,self.y + scaled_vec.v)# 比较点是否相等def __eq__(self, other):if self is other:return Trueif not isinstance(other, Point):return Falsereturn nums.are_close_enough(self.x, other.x) and \nums.are_close_enough(self.y, other.y)def __str__(self):return f'({self.x},{self.y})'

向量

# geom2d/vector.pyimport mathfrom geom2d import numsclass Vector:def __init__(self, u, v):self.u = uself.v = v# 向量的加法def __add__(self, other):return Vector(self.u+other.u,self.v+other.v)# 向量的减法def __sub__(self, other):return Vector(self.u-other.u,self.v-other.v)# 向量的缩放def scaled_by(self,factor):return Vector(factor*self.u,factor*self.v)# 计算向量的范数@propertydef norm(self):return math.sqrt(self.u**2+self.v**2)# 验证向量是否为单位向量@propertydef is_normal(self):return nums.is_close_to_one(self.norm)# 计算单位长度的向量def normalized(self):return self.scaled_by(1.0/self.norm)# 计算指定长度的向量def with_length(self,length):return self.normalized().scaled_by(length)# 向量的投影def projection_over(self,direction):return self.dot(direction.normalized())# 向量点乘def dot(self,other):return (self.u*other.u)+(self.v*other.v)# 向量叉乘def cross(self,other):return (self.u*other.v)-(self.v*other.u)# 检验两向量是否平行，即叉乘是否为0def is_parallel_to(self,other):return nums.is_close_to_zero(self.cross(other))# 检验两向量是否垂直，即点乘是否为0def is_perpendicular_to(self,other):return nums.is_close_to_zero(self.dot(other))# 向量的夹角（角度值）def angle_value_to(self,other):dot_product=self.dot(other)  # 计算点乘值norm_product=self.norm*other.norm # 范数的乘积return math.acos(dot_product/norm_product) # （点乘值/范数乘积）取反余弦，即角度值# 向量的夹角（带叉乘符号的角度值）def angle_to(self,other):value=self.angle_value_to(other)cross_product=self.cross(other)return math.copysign(value,cross_product) #math.copysign(x, y)函数返回x的大小和y的符号# 向量的旋转,旋转一定角度def rotated_radians(self,radians):cos=math.cos(radians)sin=math.sin(radians)return Vector(self.u*cos-self.v*sin,self.u*sin+self.v*cos)# 垂直向量，旋转90度def perpendicular(self):return Vector(-self.v,self.u)# 相反向量，旋转180度def opposite(self):return Vector(-self.u,-self.v)# 向量的正旋和余弦@propertydef sine(self):return self.v/self.norm@propertydef cosine(self):return self.u/self.norm# 比较向量是否相等def __eq__(self, other):# 检查是否在比较相同的实例if self is other:return True# other不是Vector类的实例if not isinstance(other,Vector):return Falsereturn nums.are_close_enough(self.u,other.u) and \nums.are_close_enough(self.v,other.v)def __str__(self):return f'({self.u},{self.v}) with norm {self.norm}'

#geom2d/vectors.py
# 向量工厂from geom2d.point import Point
from geom2d.vector import Vector# 创建一个从点p到点q的向量
def make_vector_between(p:Point,q:Point):return q-p# 创建单位方向向量
def make_versor(u:float,v:float):return Vector(u,v).normalized()# 在两点之间创建一个单位方向向量
def make_versor_between(p:Point,q:Point):return make_vector_between(p,q).normalized()

向量范数

向量的范数(norm)是指它的长度。单位范数的长度为一个单位。拥有单位范数的向量在确认向量方向时非常有用，因此，我们经常会想知道一个向量的范数是否为单位范数（它是否是单位向量）。我们也经常需要归一化(normalize)一个向量：方向不变，长度变为1。

向量点乘

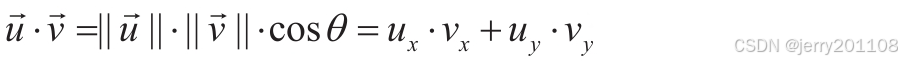
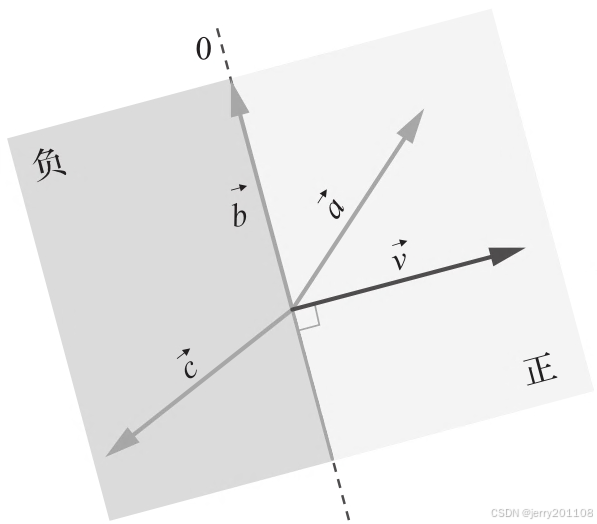
点乘(dot product)会得到一个标量，它可以反映两个向量方向的差异。

图上有一个参考向量 $\vec{v}$ 和另外三个向量： $\vec{a}$ 、 $\vec{b}$ 和 $\vec{c}$ 。一条垂直于 $\vec{v}$ 的直线将空间分成两个半平面。向量 $\vec{b}$ 在直线上，因此 $\vec{v}$ 和 $\vec{b}$ 的夹角θ等于90°。而cos(90°)=0，因此 $\vec{v}\cdot\vec{b}=0$ 。垂直向量的点乘为零。向量 $\vec{a}$ 所在的半平面和 $\vec{v}$ 相同，因此， $\vec{v}\cdot\vec{a}> 0$ 。最后， $\vec{c}$ 在与 $\vec{v}$ 相对的半平面上，因此， $\vec{v}\cdot\vec{c}< 0$ 。

向量叉乘

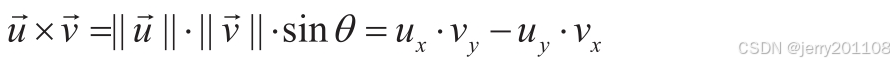
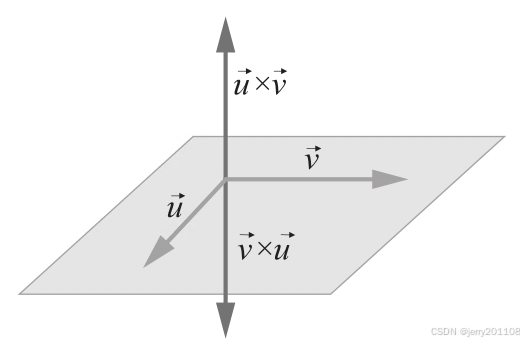
向量叉乘(cross product)会得到一个垂直于这两个向量所在平面的新向量。向量的顺序很重要，它决定了结果向量的方向。可以使用右手法则得到叉乘的方向。

叉乘不满足交换律： $\vec{u}\times \vec{v}= - \vec{v}\times \vec{u}$

二维向量叉乘的一个重要应用是确定角度的旋转方向。 $\vec{u}\times \vec{v}> 0$ ，因为从 $\vec{u}$ 到 $\vec{v}$ 的角度为正（逆时针）。相反，从 $\vec{v}$ 到 $\vec{u}$ 的角度为负，因此叉乘 $\vec{v}\times \vec{u}< 0$ 。最后，平行向量的叉乘为0，这很显然，因为sin 0=0。

向量旋转

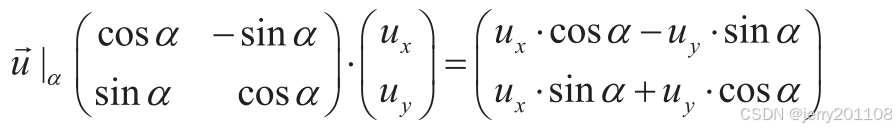
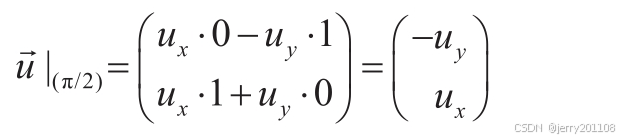
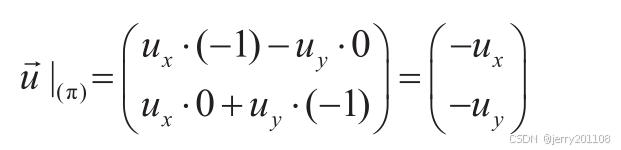
cos(π/2)=0, sin(π/2)=1，cos(π)=-1, sin(π)=0

向量的正弦和余弦

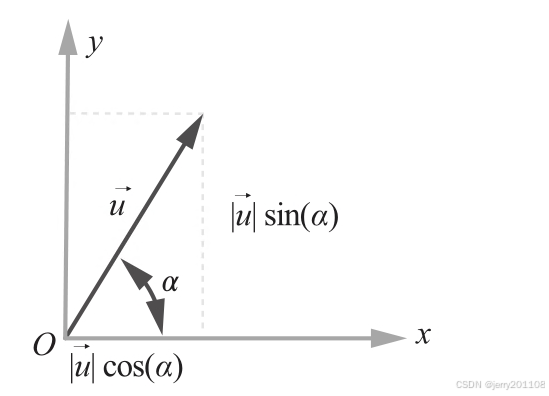
三、直线和线段

线段

# geom2d/segment.pyfrom geom2d.point import Point
from geom2d.vectors import make_vector_between,make_versor_between
from geom2d import tparamclass Segment:def __init__(self,start:Point,end:Point):self.start=startself.end=end# 线段的方向向量@propertydef direction_vector(self):return make_vector_between(self.start,self.end)# 线段的单位方向向量@propertydef direction_versor(self):return make_versor_between(self.start,self.end)# 垂直于线段方向的向量，法向量# 调用self的direction_versor来得到线段的方向向量，同时也是Vector类的实例# 调用perpendicular方法，返回垂直于线段方向的向量def normal_versor(self):return self.direction_versor.perpendicular()# 线段的长度@propertydef length(self):return self.start.distance_to(self.end)# 使用参数t获取线段上的任意一点def point_at(self,t:float):tparam.ensure_valid(t)  # 验证t值return self.start.displaced(self.direction_vector,t)# 线段的中点@propertydef middle(self):return self.point_at(tparam.MIDDLE)# 线段上的最近点# 计算从线段的端点S到外部点P的向量v# 计算在线段方向上投影的单位向量d# 将投影的长度设为vsdef closest_point_to(self,p:Point):v=make_vector_between(self.start,p)d=self.direction_versorvs=v.projection_over(d)if vs<0:return self.startif vs>self.length:return self.endreturn self.start.displaced(d,vs)

线段的方向向量

方向(direction)是线段的一个重要性质，定义为从起点S到终点E的向量。用 $\vec{d}$ 来表示该向量。

方向向量(direction vector)是一个与线段平行且长度相同的向量，其方向是从起点到终点。

单位方向(direction versor)是方向向量的归一化版本，即与方向向量的方向相同，但长度为一个单位。

垂直于线段的方向也同样重要。将单位方向向量 $\hat{d}$ 旋转方向π/4 rad(90°)，就可以得到线段的单位法向量(normalversor)。

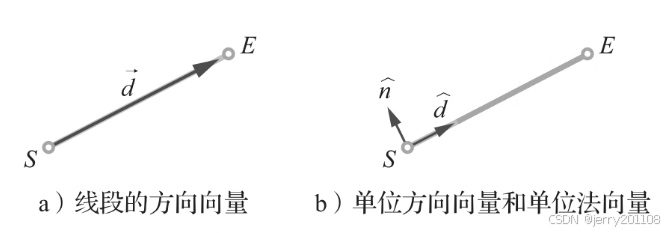
线段上最接近外部点的点

如果外部点没有与线段对齐，穿过该点且垂直于线段的直线不与线段相交，那么最近的点必然是两个端点S或E中的一个。

如果该点与该段对齐，则垂直线与线段的交点就是最近的点。

如图：点S≡A'是离A最近的点，点E≡B'是最接近B的点，C'是最接近C的点。

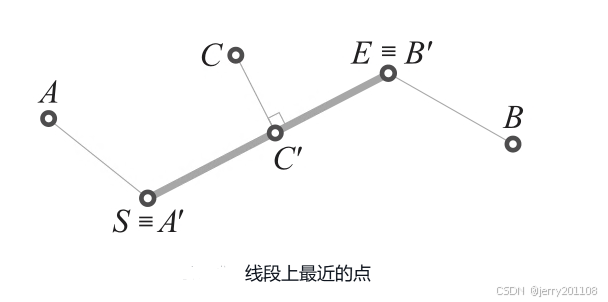
线段的交点

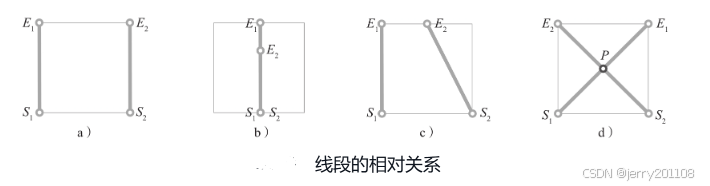
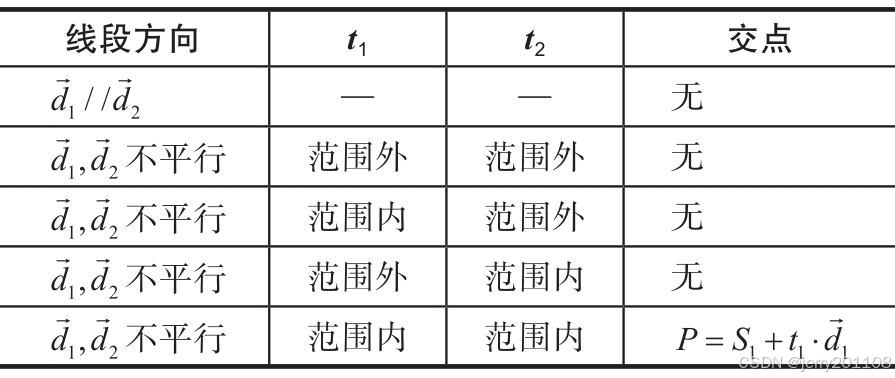
四、多边形

一般多边形——用它们的顶点来定义；

圆是平面内与指定点（圆心）的距离（半径）相同的所有点的集合。因此，圆由圆心C的位置和半径R的值定义

矩形——由原点、宽度和高度定义

多边形中一个重要性质是质心(centroid)，即所有顶点坐标的算术平均值。

五、仿射变换

仿射变换：它使我们能够通过缩放、旋转、平移和剪切来改变几何形状。

六、单元测试

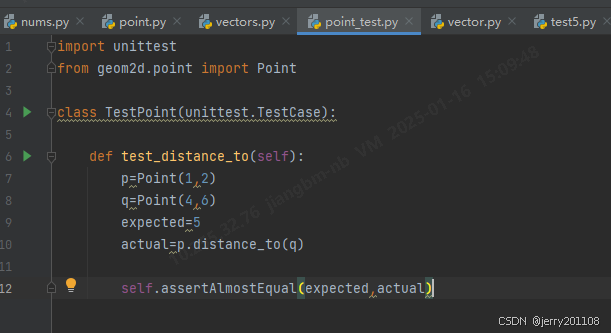
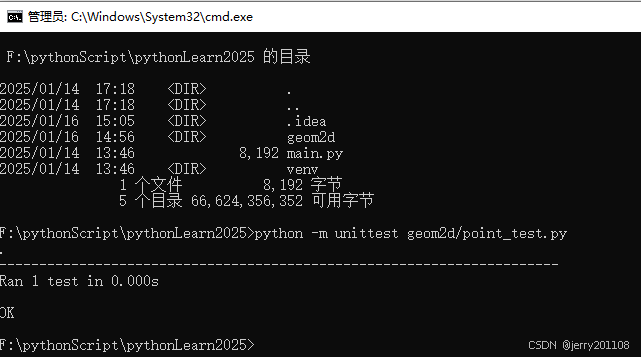
断言方法

断言方法	描述
assertAlmostEqual	定义在我们引用的类unittest.TestCase中，用指定的公差来检查浮点数是否相等，公差用小数点后的位数表示，默认是7。请记住，在比较浮点数时，必须有公差，或者像上述例子，给定小数点后的位数
assertEqual	使用==操作符来比较这两个参数
assertTrue	检验给定表达式的计算结果是否为True
assertFalse	检验给定表达式的计算结果是否为False
assertRaises	向其传入三个参数。首先是预期要触发的异常(TParamError)。其次，传入了期望触发异常的方法。最后，传入需要传递给前面的方法（在本例中为point_at）的实参。
assertIsNone	检查传入的值是否是None（无）