发现宝藏

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。【宝藏入口】。

---

第十二届蓝桥杯大赛软件赛省赛 Java A 组

---

【考生须知】

考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。

考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后，将无法继续提交或浏览答案。

对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。

选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。

试题包含 “结果填空” 和 “程序设计” 两种题型。

结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。

程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。

注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。

所有源码必须在同一文件中。调试通过后，拷贝提交。

注意: 不要使用 package 语句。

注意：选手代码的主类名必须为: Main, 否则会被判为无效代码。

注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。

---

试题 A: 相乘

本题总分: 5 分

【问题描述】

小蓝发现, 他将 1 至 1000000007 之间的不同的数与 2021 相乘后再求除以 1000000007 的余数, 会得到不同的数。

小蓝想知道, 能不能在 1 至 1000000007 之间找到一个数, 与 2021 相乘后再除以 1000000007 后的余数为 999999999 。如果存在, 请在答案中提交这个数:如果不存在, 请在答案中提交 0 。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 B: 直线

本题总分: 5 分

【问题描述】

在平面直角坐标系中, 两点可以确定一条直线。如果有多点在一条直线上,那么这些点中任意两点确定的直线是同一条。

给定平面上 $2\times 3$ 个整点 $\{(x,y)\mid 0\le x<2,0\le y<3,x\in Z,y\in Z\}$, 即横坐标是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2 ) 之间的整数的点。这些点一共确定了 11 条不同的直线。

给定平面上 $20\times 21$ 个整点 $\{(x,y)\mid 0\le x<20,0\le y<21,x\in Z,y\in Z\}$, 即横坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20 ) 之间的整数的点。请问这些点一共确定了多少条不同的直线。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 $\mathrm{C}:$ 货物摆放

本题总分: 10 分

【问题描述】

小蓝有一个超大的仓库, 可以摆放很多货物。

现在, 小蓝有 $n$ 箱货物要摆放在仓库, 每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向, 每箱货物的边都必须严格平行于长、宽、高。

小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 $L、W、H$ 的货物, 满足 $n=L\times W\times H$ 。

给定 $n$, 请问有多少种堆放货物的方案满足要求。

例如, 当 $n=4$ 时, 有以下 6 种方案: $1\times 1\times 4、1\times 2\times 2、1\times 4\times 1、2\times 1\times 2$ 、 $2\times 2\times 1、4\times 1\times 1$ 。

请问, 当 $n=2021041820210418$ (注意有 16 位数字) 时, 总共有多少种方案?

提示: 建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的題, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 D: 路径

本题总分: 10 分

【问题描述】

小蓝学习了最短路径之后特别高兴, 他定义了一个特别的图, 希望找到图中的最短路径。

小蓝的图由 2021 个结点组成, 依次编号 1 至 2021。

对于两个不同的结点 $a,b$, 如果 $a$ 和 $b$ 的差的绝对值大于 21 , 则两个结点之间没有边相连; 如果 $a$ 和 $b$ 的差的绝对值小于等于 21 , 则两个点之间有一条长度为 $a$ 和 $b$ 的最小公倍数的无向边相连。

例如: 结点 1 和结点 23 之间没有边相连: 结点 3 和结点 24 之间有一条无向边, 长度为 24 ; 结点 15 和结点 25 之间有一条无向边, 长度为 75 。

请计算, 结点 1 和结点 2021 之间的最短路径长度是多少。

提示: 建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 E: 回路计数

本题总分: 15 分

【问题描述】

蓝桥学院由 21 栋教学楼组成, 教学楼编号 1 到 21。对于两栋教学楼 $a$ 和 $b$, 当 $a$ 和 $b$ 互质时, $a$ 和 $b$ 之间有一条走廊直接相连, 两个方向皆可通行, 否则没有直接连接的走廊。

小蓝现在在第一栋教学楼, 他想要访问每栋教学楼正好一次, 最终回到第一标教学楼（即走一条哈密尔顿回路），请问他有多少种不同的访问方案？两个访问方案不同是指存在某个 $i$, 小蓝在两个访问方法中访问完教学楼 $i$ 后访问了不同的教学楼。

提示: 建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 $\mathrm{F}:$ 最少砝码

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 15 分

【问题描述】

你有一架天平。现在你要设计一套砝码, 使得利用这些砝码可以称出任意小于等于 $N$ 的正整数重量。

那么这套砝码最少需要包含多少个砝码?

注意砝码可以放在天平两边。

【输入格式】

输入包含一个正整数 $N$ 。

【输出格式】

输出一个整数代表答案。

【样例输入】

$\begin{array}{l}7\end{array}$

【样例输出】

$\begin{array}{l}3\end{array}$

【样例说明】

3 个砝码重量是 $1、4、6$, 可以称出 1 至 7 的所有重量。

$1=1$;

$2=6-4($ 天平一边放 6 , 另一边放 4$)$;

$3=4-1;$

$4=4$

$5=6-1$;

$6=6$;

$7=1+6;$

少于 3 个砝码不可能称出 1 至 7 的所有重量。

【评测用例规模与约定】

对于所有评测用例， $1\le N\le 1000000000$ 。

---

试题 G: 左孩子右兄弟

时间限制: $3.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 20 分

【问题描述】

对于一柦多叉树, 我们可以通过 “左孩子右兄弟” 表示法, 将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的, 那么得到的二叉树可能不唯一。换句话说, 每个结点可以选任意子结点作为左孩子, 并按任意顺序连接右兄弟。给定一棵包含 $N$ 个结点的多叉树, 结点从 1 至 $N$ 编号, 其中 1 号结点是根, 每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树, 高度最高是多少。注: 只有根结点这一个结点的树高度为 0 。

例如如下的多叉树:

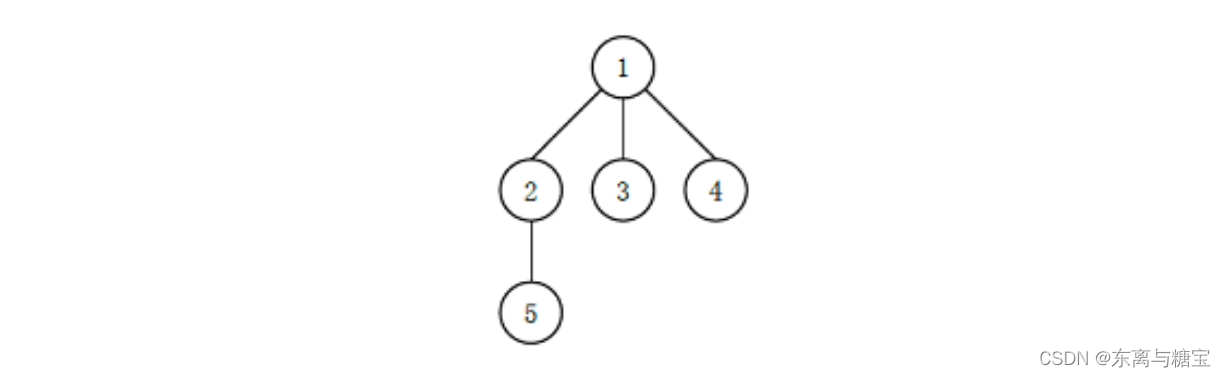
可能有以下 3 种 (这里只列出 3 种, 并不是全部) 不同的 “左孩子右兄弟”表示:

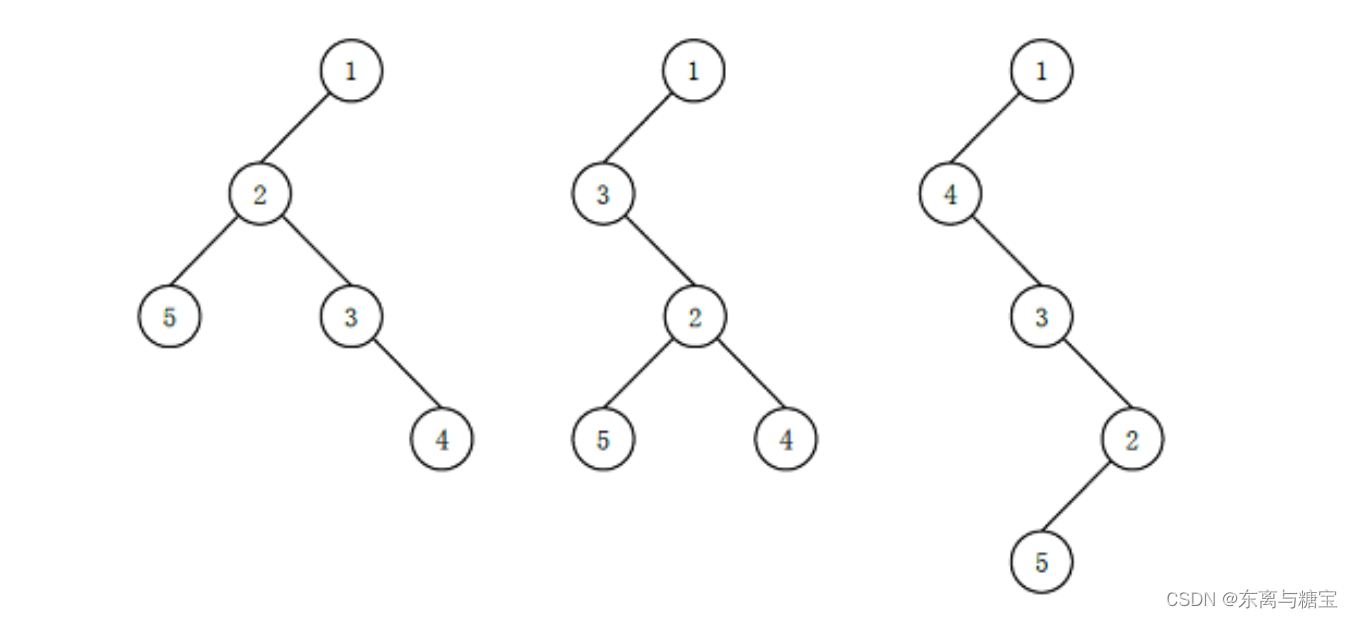
其中最后一种高度最高, 为 4 。

【输入格式】

输入的第一行包含一个整数 $N$ 。

以下 $N-1$ 行, 每行包含一个整数, 依次表示 2 至 $N$ 号结点的父结点编号。

【输出格式】

输出一个整数表示答案。

【样例输入】

$\begin{array}{l}5\end{array}$

$\begin{array}{l}1\end{array}$

$\begin{array}{l}1\end{array}$

$\begin{array}{l}1\end{array}$

$\begin{array}{l}2\end{array}$

【样例输出】

$\begin{array}{l}4\end{array}$

【评测用例规模与约定】

对于 $30\%$ 的评测用例, $1\le N\le 20$;

对于所有评测用例, $1\le N\le 100000$ 。

---

试题 $\mathrm{H}:$ 异或数列

时间限制: $2.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 20 分

【问题描述】

Alice 和 Bob 正在玩一个异或数列的游戏。初始时, Alice 和 Bob 分别有一个整数 $a$ 和 $b$, 初始值均为 0 。有一个给定的长度为 $n$ 的公共数列 $X_1,X_2,\cdots ,X_n$ 。

Alice 和 Bob 轮流操作, Alice 先手, 每步可以在以下两种选项中选一种:

选项 1: 从数列中选一个 $X_i$ 给 Alice 的数异或上, 或者说令 $a$ 变为 $a\oplus$ $X_i$ 。(其中 $\oplus$ 表示按位异或)

选项 2: 从数列中选一个 $X_i$ 给 Bob 的数异或上, 或者说令 $b$ 变为 $b\oplus X_i$ 。

每个数 $X_i$ 都只能用一次, 当所有 $X_i$ 均被使用后 ( $n$ 轮后) 游戏结束。游戏结束时, 拥有的数比较大的一方获胜, 如果双方数值相同, 即为平手。

现在双方都足够㴔明, 都采用最优策略, 请问谁能获胜?

【输入格式】

每个评测用例包含多组询问。询问之间彼此独立。

输入的第一行包含一个整数 $T$, 表示询问数。

接下来 $T$ 行每行包含一组询问。其中第 $i$ 行的第一个整数 $n_i$ 表示数列长度, 随后 $n_i$ 个整数 $X_1,X_2,\cdots ,X_{ni}$ 表示数列中的每个数。

【输出格式】

输出 $T$ 行, 依次对应每组询问的答案。

每行包含一个整数 $1、0$ 或 -1 分别表示 Alice 胜、平局或败。

【样例输入】

$\begin{array}{l}4\end{array}$

$\begin{array}{ll}1& 1\end{array}$

$\begin{array}{ll}1& 0\end{array}$

$\begin{array}{lll}2& 2& 1\end{array}$

$\begin{array}{llllllll}7& 992438& 1006399& 781139& 985280& 4729& 872779& 563580\end{array}$

【样例输出】

【评测用例规模与约定】

对于所有评测用例, $1\le T\le 200000,1\le {\sum }_{i=1}^T{n}_i\le 200000,0\le X_i<2^{20}$ 。

---

试题 $\mathbf{I}$ 双向排序

时间限制: $5.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 25 分

【问题描述】

给定序列 $\left(a_1,a_2,\cdots ,a_n\right)=(1,2,\cdots ,n)$, 即 $a_i=i_{。}$

小蓝将对这个序列进行 $m$ 次操作, 每次可能是将 $a_1,a_2,\cdots ,a_{q_i}$ 降序排列,或者将 $a_{q,},a_{q_i+1},\cdots ,a_n$ 升序排列。

请求出操作完成后的序列。

【输入格式】

输入的第一行包含两个整数 $n,m$, 分别表示序列的长度和操作次数。

接下来 $m$ 行描述对序列的操作, 其中第 $i$ 行包含两个整数 $p_i,q_i$ 表示操作类型和参数。当 $p_i=0$ 时, 表示将 $a_1,a_2,\cdots ,a_{qi}$ 降序排列; 当 $p_i=1$ 时, 表示将 $a_{q_i},a_{q_i+1},\cdots ,a_n$ 升序排列。

【输出格式】

输出一行, 包含 $n$ 个整数, 相邻的整数之间使用一个空格分隔, 表示操作完成后的序列。

【样例输入】

$\begin{array}{ll}3& 3\end{array}$

$\begin{array}{ll}0& 3\end{array}$

$\begin{array}{ll}1& 2\end{array}$

$\begin{array}{ll}0& 2\end{array}$

【样例输出】

$\begin{array}{lll}3& 1& 2\end{array}$

【样例说明】

原数列为 $(1,2,3)$ 。

第 1 步后为 $(3,2,1)$ 。

第 2 步后为 $(3,1,2)$ 。

第 3 步后为 $(3,1,2)$ 。与第 2 步操作后相同, 因为前两个数已经是降序了。

【评测用例规模与约定】

对于 $30\%$ 的评测用例, $n,m\le 1000$;

对于 $60\%$ 的评测用例, $n,m\le 5000$;

对于所有评测用例， $1\le n,m\le 100000,0\le p_i\le 1,1\le q_i\le n_{\text{。 }}$

---

试题 $\mathrm{J}:$ 分果果

时间限制: $10.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 25 分

【问题描述】

小蓝要在自己的生日宴会上将 $n$ 包糖果分给 $m$ 个小朋友。每包糖果都要分出去, 每个小朋友至少要分一包, 也可以分多包。

小蓝已经提前将糖果准备好了, 为了在宴会当天能把糖果分得更平均一些,小蓝要先计算好分配方案。

小蓝将榶果从 1 到 $n$ 编号, 第 $i$ 包榶果重 $w_i$ 。 小朋友从 1 到 $m$ 编号。每个小朋友只能分到编号连续的糖果。小蓝想了很久没想出合适的分配方案使得每个小朋友分到的糖果差不多重。因此需要你帮他一起想办法。为了更好的分配糖果, 他可以再买一些糖果, 让某一些编号的糖果有两份。当某个编号的糖果有两份时, 一个小朋友最多只能分其中的一份。

请找一个方案, 使得小朋友分到的糖果的最大重量和最小重量的差最小,请输出这个差。

例如, 小蓝现在有 5 包榶果, 重量分别为 $6,1,2,7,9$, 如果小蓝要分给两个小朋友, 则他可以将所有榶果再买一份, 两个小朋友都分到 1 至 5 包榶果,重量都是 25 , 差为 0 。

再如, 小蓝现在有 5 包糖果, 重量分别为 $6,1,2,7,9$, 如果小蓝要分给三个小朋友, 则他可以将第 3 包糖果再买一份, 第一个小朋友分 1 至 3 包, 第二个小朋友分 3 至 4 包, 第三个小朋友分第 5 包, 每个小朋友分到的重量都是 9 ,差为 0 。

再如, 小蓝现在有 5 包桮果, 重量分别为 $6,1,2,7,9$, 如果小蓝要分给四个小朋友, 则他可以将第 3 包和第 5 包糖果再买一份, 仍然可以每个小朋友分到的重量都是 9 , 差为 0 。

再如, 小蓝现在有 5 包糖果, 重量分别为 $6,1,2,7,9$, 如果小蓝要分给五个小朋友, 则他可以将第 4 包和第 5 包糖果再买一份, 第一个小朋友分第 1 至 2 包重量为 7 , 第二个小朋友分第 3 至 4 包重量为 9 , 第三个小朋友分第 4 包重量为 7 , 第四个和第五个小朋友都分第 5 包重量为 9 。差为 2 。

【输入格式】

输入第一行包含两个整数 $n$ 和 $m$, 分别表示糖果包数和小朋友数量。

第二行包含 $n$ 个整数 $w_1,w_2,\cdots ,w_n$, 表示每包糖果的重量。

【输出格式】

输出一个整数, 表示在最优情况下小朋友分到的糖果的最大重量和最小重量的差。

【样例输入 1】

$\begin{array}{ll}5& 2\end{array}$

$\begin{array}{lllll}6& 1& 2& 7& 9\end{array}$

【样例输出 1】

$\begin{array}{l}0\end{array}$

【样例输入 2】

$\begin{array}{ll}5& 5\end{array}$

$\begin{array}{lllll}6& 1& 2& 7& 9\end{array}$

【样例输出 2】

$\begin{array}{l}2\end{array}$

【评测用例规模与约定】

对于 $30\%$ 的评测用例, $1\le n\le 10,1\le m\le 10,1\le w_i\le 10$;

对于 $60\%$ 的评测用例, $1\le n\le 30,1\le m\le 20,1\le w_i\le 30$;

对于所有评测用例, $1\le n\le 100,1\le m\le 50,1\le w_i\le 100$ 。在评测数据中, $w_i$ 随机生成, 在某个区间均匀分布。