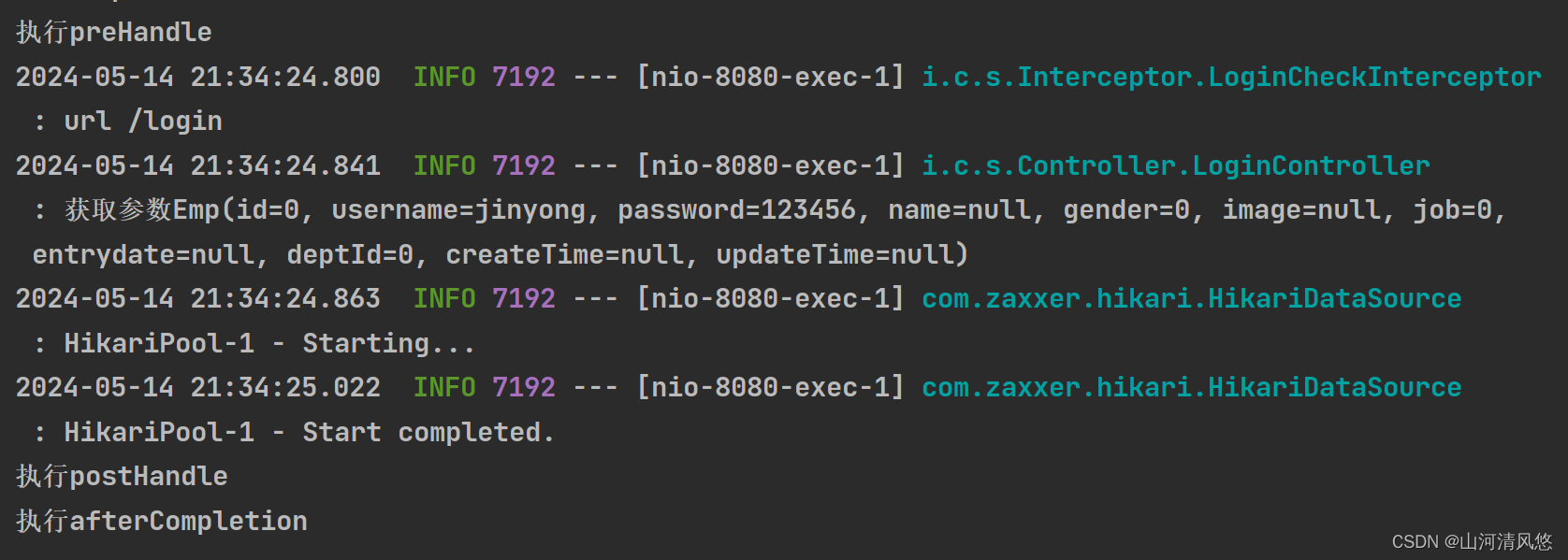
大模型席卷全球，彷佛得模型者得天下。对于IT行业来说，以后可能没有各种软件了，只有各种各样的智体（Agent）调用各种各样的API。在这种大势下，笔者也阅读了很多大模型相关的资料，和很多新手一样，开始脑子里都是一团乱麻，随着相关文章越读越多，再进行内容梳理，终于理清了一条清晰的脉络。笔者希望通过三篇文章总结（入门篇、原理篇和应用篇）将思路写下来，以便跟我一样的新手读者快速了解大模型的方方面面。在这里，笔者先强调一下，本系列文章的深度有限，只是个人对大模型知识脉络的梳理，同时也会借鉴一下同行的博客内容充实本文，文末将会注明参考来源。

笔者写原理篇时心情是有些惴惴不安的，因为毕竟对大模型的研究有限，缺乏深度。但是，还是觉得有必要记录一下学习理解心得，权当自己的学习笔记吧！如果本文有疏漏，敬请留言指正，勿喷，谢谢！

大模型架构

要说清楚大模型的原理，必须先大致了解大模型的架构。在上一篇文章中的分类中提高，大模型基本都是采用的Transformer架构，而该架构整体可以分为四个部分：

• 输入（Input）：对输入的内容进行向量化，计算机只能对数字进行计算和转换；
• 编码器（Encoders）：通过自注意力机制，将输入内容Token之间的隐含关联信息以向量的形式进行表征；
• 解码器（Decoders）：循环迭代预测下一个元素出现的概率，将本轮预测结果作为输入，进行下一轮预测。
• 输出（Output）：将预测结果进行向量化，最终得到一个矩阵。

Transformer架构图如下：

大模型原理

向量与矩阵

在正式讲解大模型原理之前，有两个数学概念需要先了解一下。

• 向量
  向量表示形式类似于数组，但是值只能为数字，如：[1,2,3,4]。
  向量用来通过一组特征来描述一个事物。比如苹果可以描述为：一种圆形的，果皮上有纹路的，味道酸甜的水果。用向量则可以表示为：[0, 1, 3, 4]，其中0表示形状值-圆形，1表示果皮是否有纹路-有，3表示口味值-酸甜，4表示物体品类-水果。
  同理，用户输入文本中的每个词也都可以用向量表示。

• 矩阵
  矩阵类似多维数组，但是值只能为数字。多个同维度向量可以组成矩阵，向量是一种特殊的矩阵。

原理阐述

通过上述对Transformer架构的描述，可以得出一个大模型的大致原理，分为两个阶段：
（1）模型训练生成阶段
通过将海量数据输入到Transformer系统中进行训练计算，最终输出一个矩阵W，这就是训练的结果 —— （大）模型。是否为大模型，需要根据参数量和数据量来判断，这两个因素也决定了模型矩阵W的维度大小。

（2）模型应用进化阶段
将用户输入的信息转化为向量X，将向量X与模型W矩阵进行计算，得到一个向量Y，再将Y反向量化为用户能看懂的信息（比如：文本）。当然，在实际的应用过程中，模型会随着用户的使用交流，得到进化，本质上是矩阵W的某些数值会发生调整。

下图是笔者理解的大模型的训练和使用原理图：

上述原理阐述中有一个比较关键的问题需要弄清楚：文本如何转化为向量？

（1）先将输入文本切换为词元Token；
（2）然后用向量对单个Token进行表示；
（3）再将词元在文本中的位置信息表示为向量；
（4）将Token本身的向量与位置向量相加，则得到了该Token的表征向量。
一个文本输入最终被转为化一个向量矩阵，但是在推理过程中，仍是对一个Token进行推理的（即与一个向量进行运算），更详细的词向量化原理可以参考文末引用的文章。以下是一个词向量化示意图：

简单总结

1. 所有喂给大模型的数据，都是需要先进行词向量化的，计算机只能通过数字计算来实现推理或思考；
2. 大模型本质上是一个维度非常巨大的矩阵；
3. 模型训练和微调本质上是调整模型矩阵的值；
4. 大模型回答用户问题，实质上是先将用户输入向量化之后，再与模型矩阵进行运算得到值最优的向量值，再将该向量值转为用户可以理解的信息返回给用户。

参考文献

• 大模型词向量：解析语义，助你成为沟通达人
• 大模型解惑
• Transformer模型详解（图解最完整版）
• 模型 · 向量和矩阵