小伙伴们大家好，本片文章将会讲解AVL树的左双选和右双旋的相关内容。


如果看到最后您觉得这篇文章写得不错，有所收获，麻烦点赞👍、收藏🌟、留下评论📝。您的支持是我最大的动力，让我们一起努力，共同成长！

---

1. 左右双旋

⚡出现情况

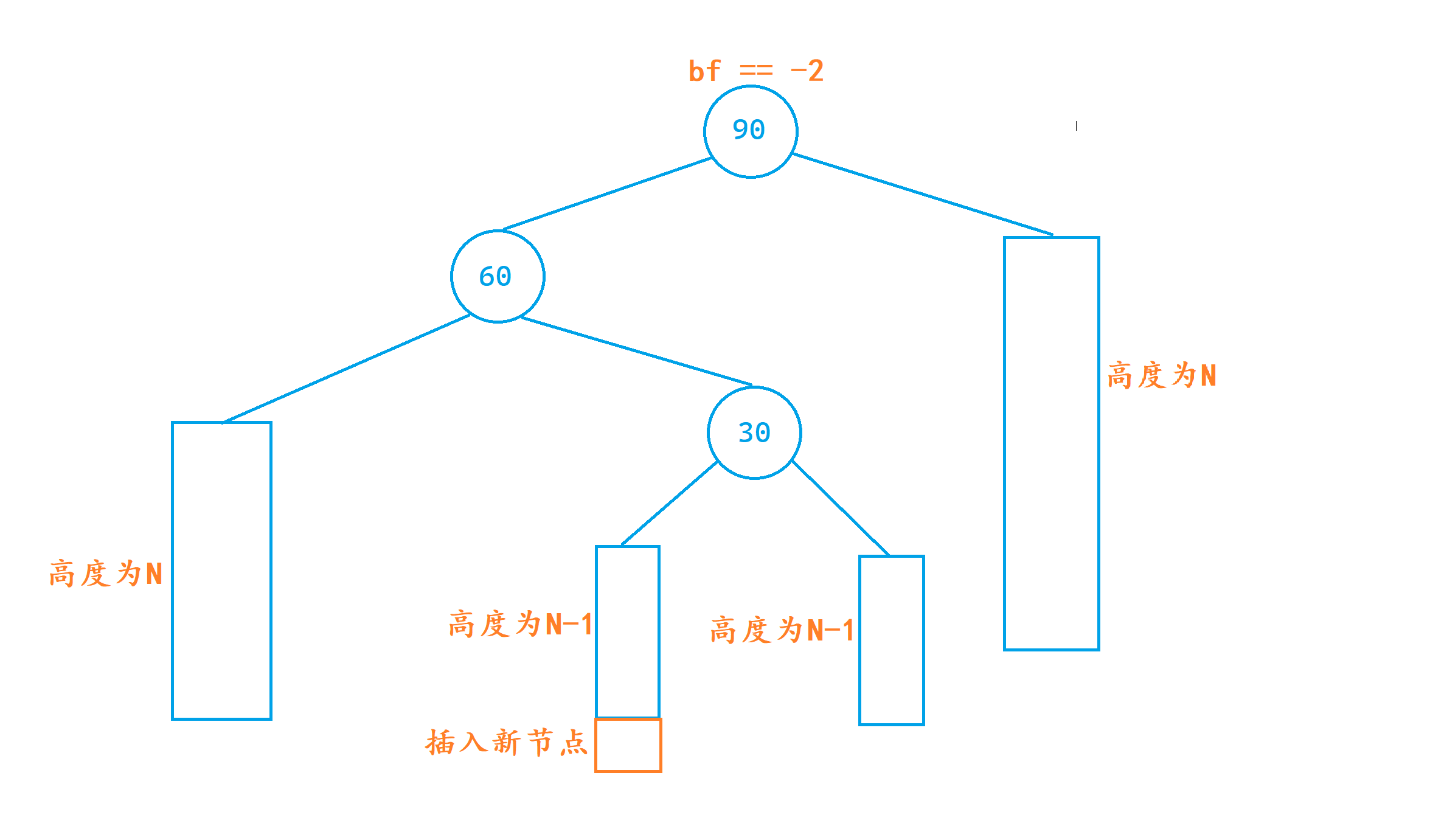
1. 此处在30的左子树或者右子树新增节点都会引发旋转；
2. 如果单纯的对根节点进行右单旋，并不能解决左边高的问题，会变成右边高，所以要进行双旋，步骤如下：

1. 先对parent->left节点进行左单旋

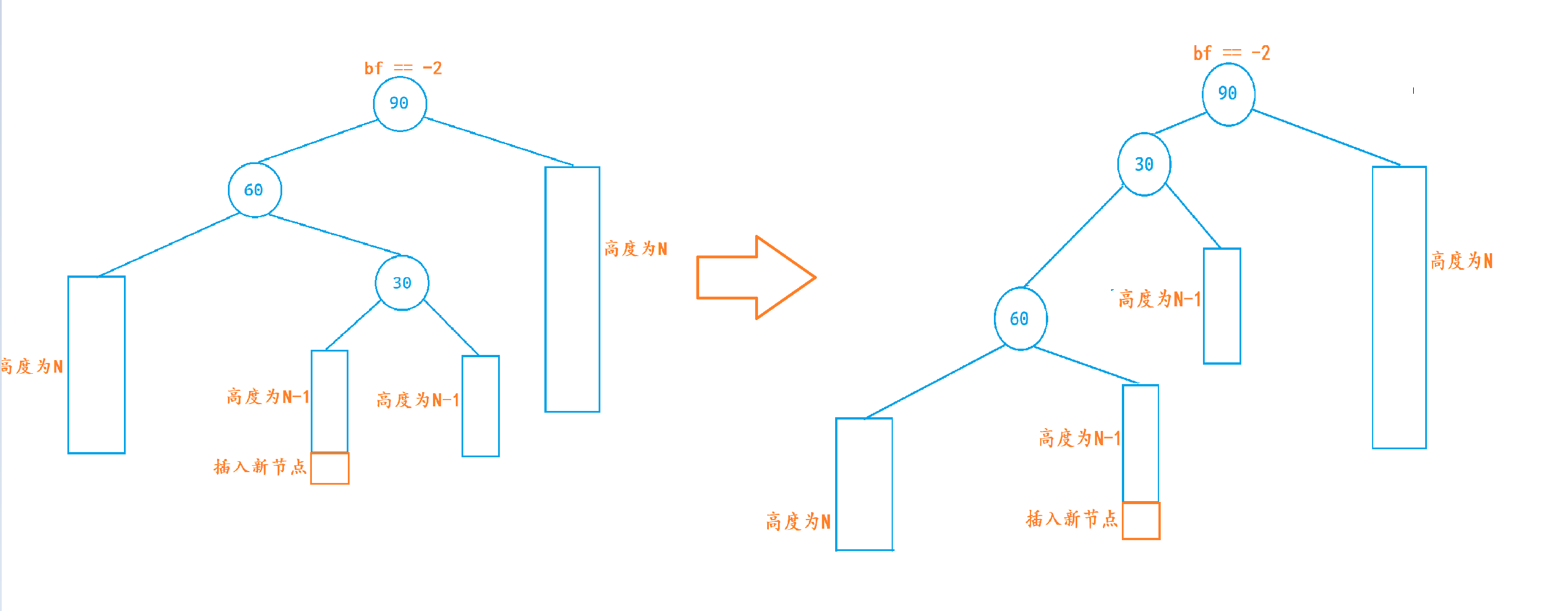
2. 再对根节点进行右单旋

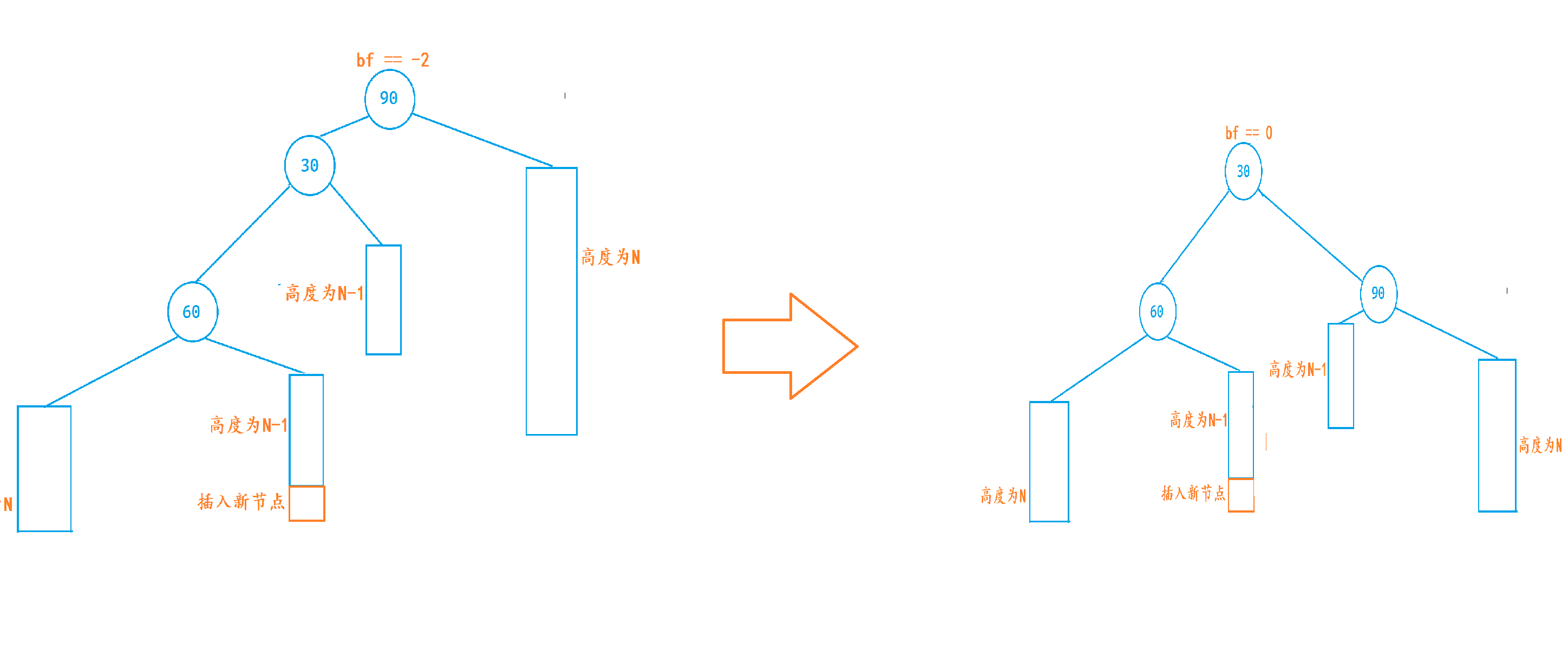
完整步骤

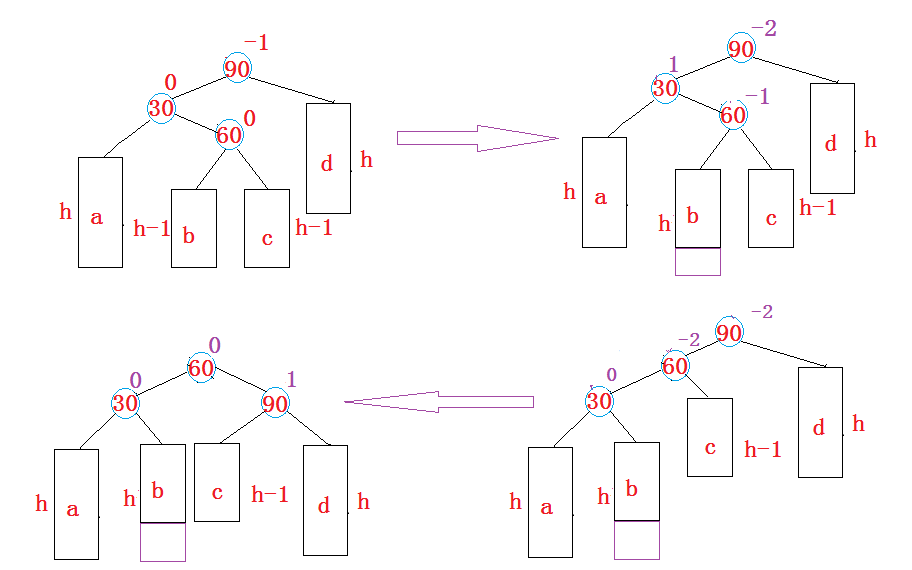
我们假设顶端节点叫做parent，parent->left 叫做subL，subL->right 叫做subLR。

左右双旋后满足二叉搜索树的性质：

左右双旋后，实际上就是让subLR的左子树和右子树，分别作为subL和parent的右子树和左子树，再让subL和parent分别作为subLR的左右子树，最后让subLR作为整个子树的根。

1. subLR的左子树当中的结点本身就比subL的值大，因此可以作为subL的右子树。

2. subLR的右子树当中的结点本身就比parent的值小，因此可以作为parent的左子树。

3. 经过步骤1、2后，subL及其子树当中结点的值都就比subLR的值小，而parent及其子树当中结点的值都就比subLR的值大，因此它们可以分别作为subLR的左右子树。

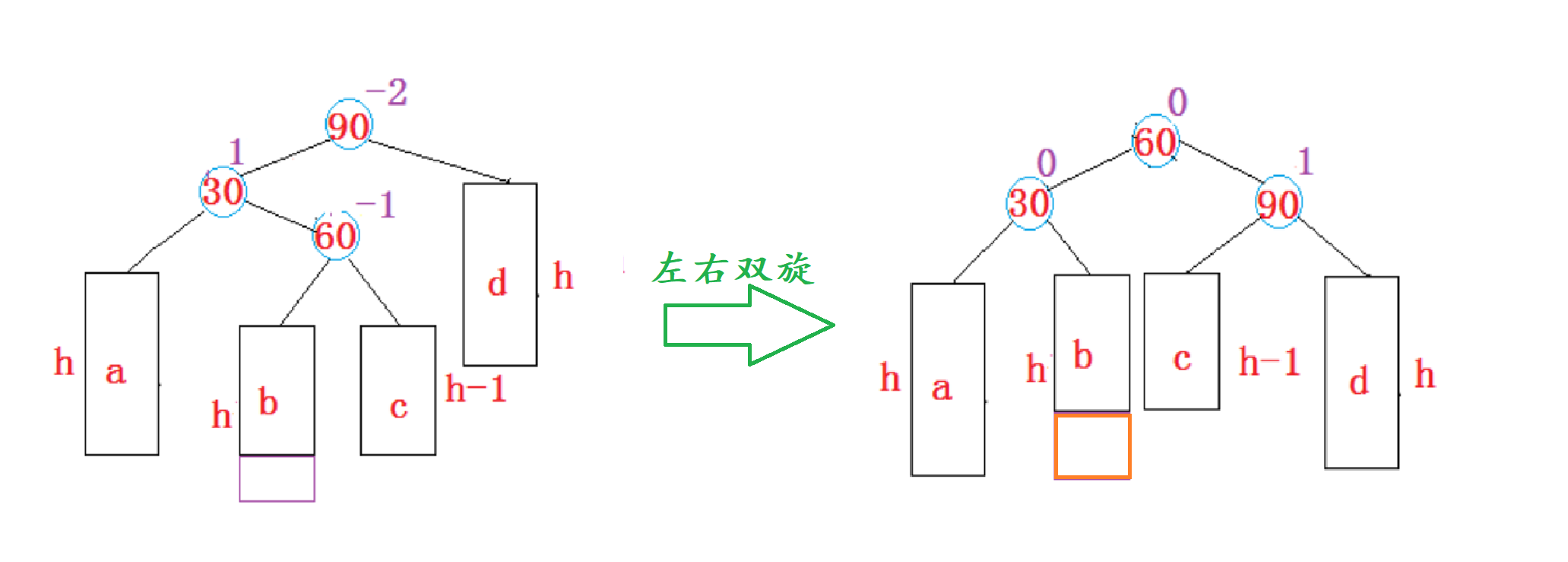
左右双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：

1、当subLR原始平衡因子是-1时，左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0。

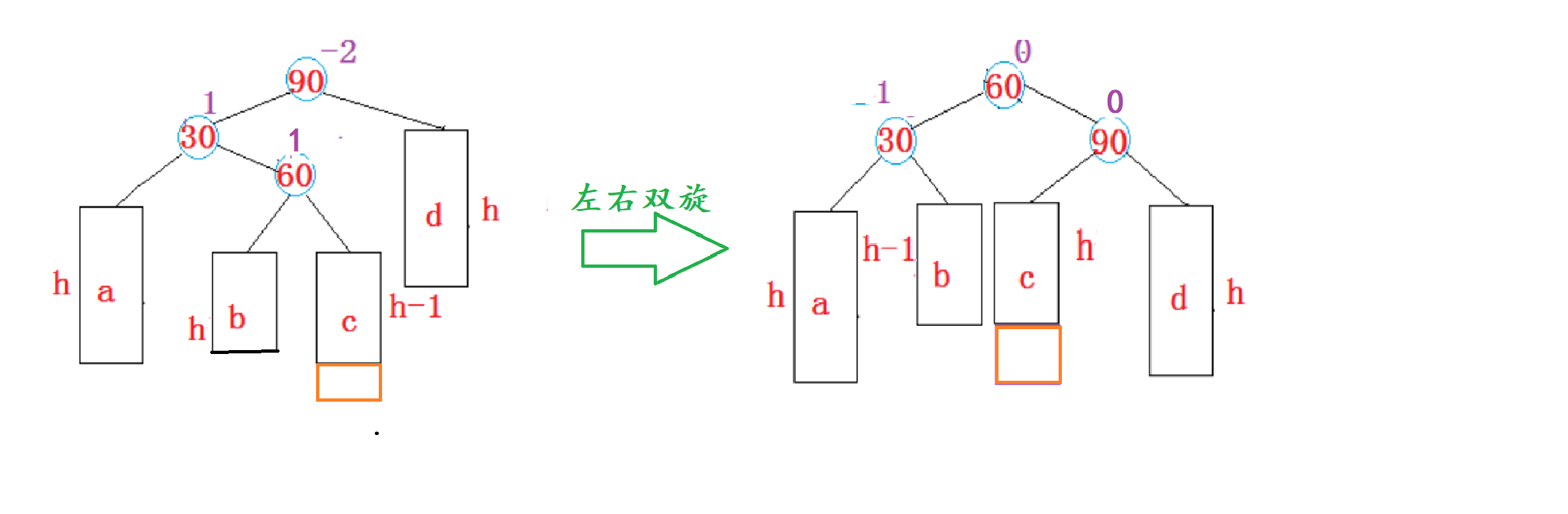
2、当subLR原始平衡因子是1时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0。

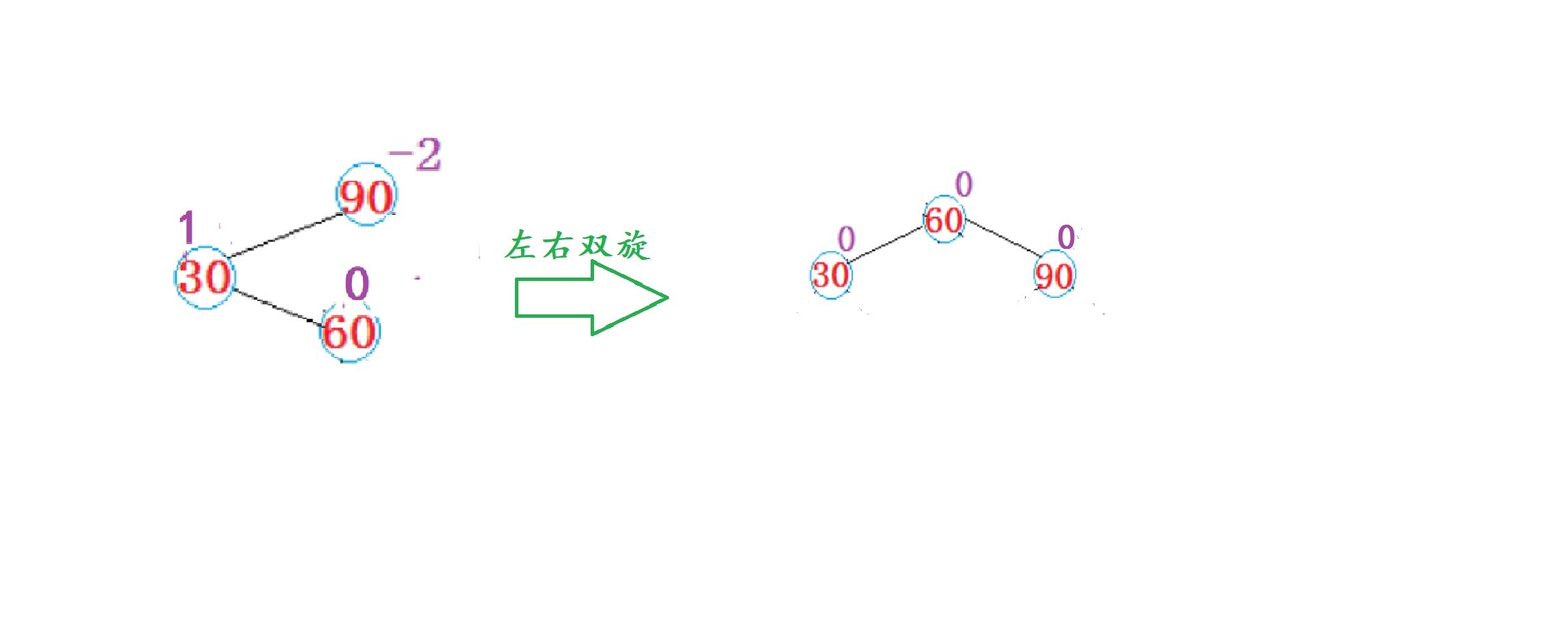
3、当subLR原始平衡因子是0时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。

代码如下：

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//1、以subL为旋转点进行左单旋RotateL(subL);//2、以parent为旋转点进行右单旋RotateR(parent);if (bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else if (bf == 0){subL->_bf = subLR->_bf = parent->_bf = 0;}else {assert(false);}
}

---

1. 右左双旋

⚡出现情况

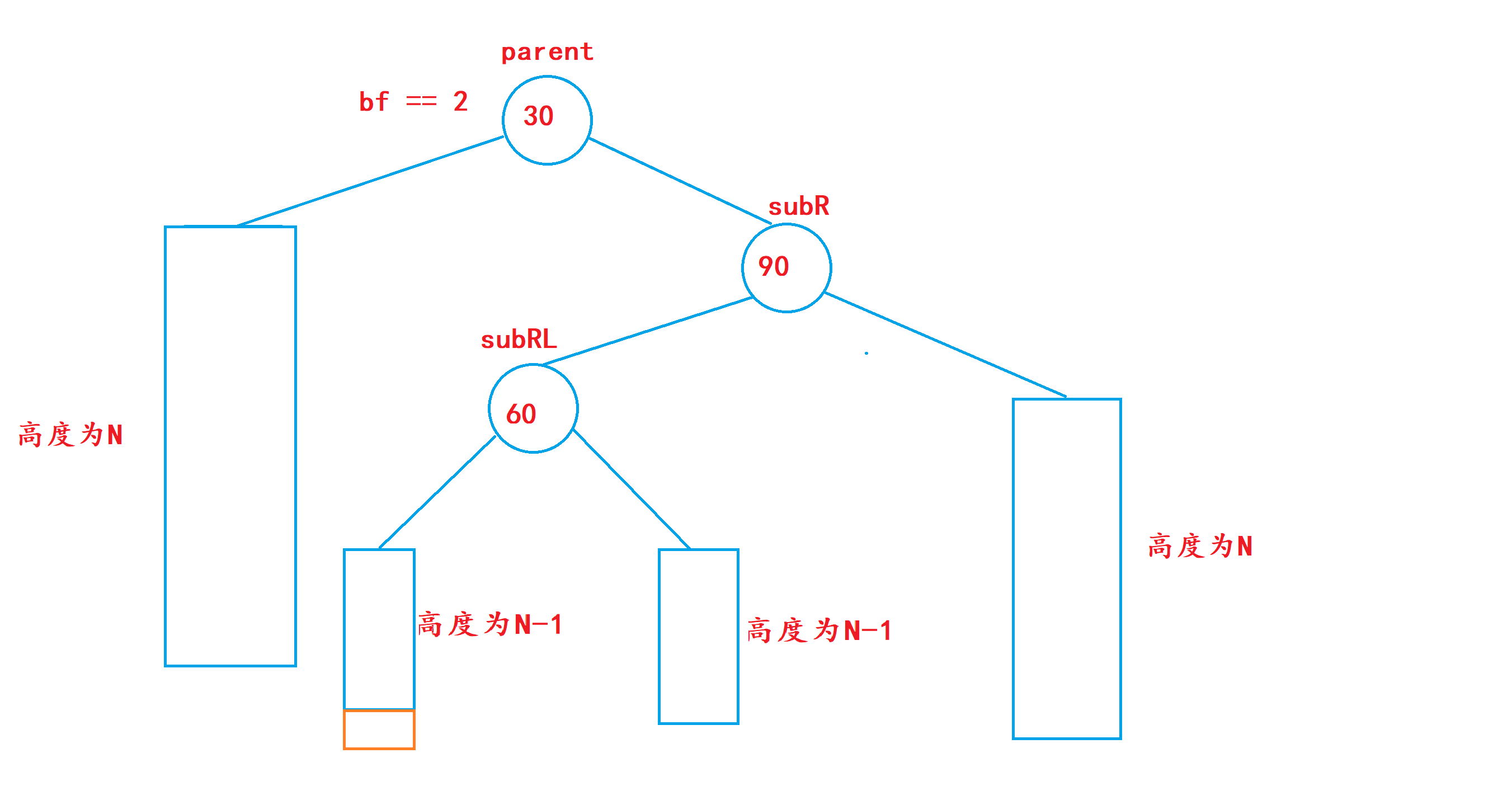
1. 此处在60的左子树或者右子树新增节点都会引发旋转；
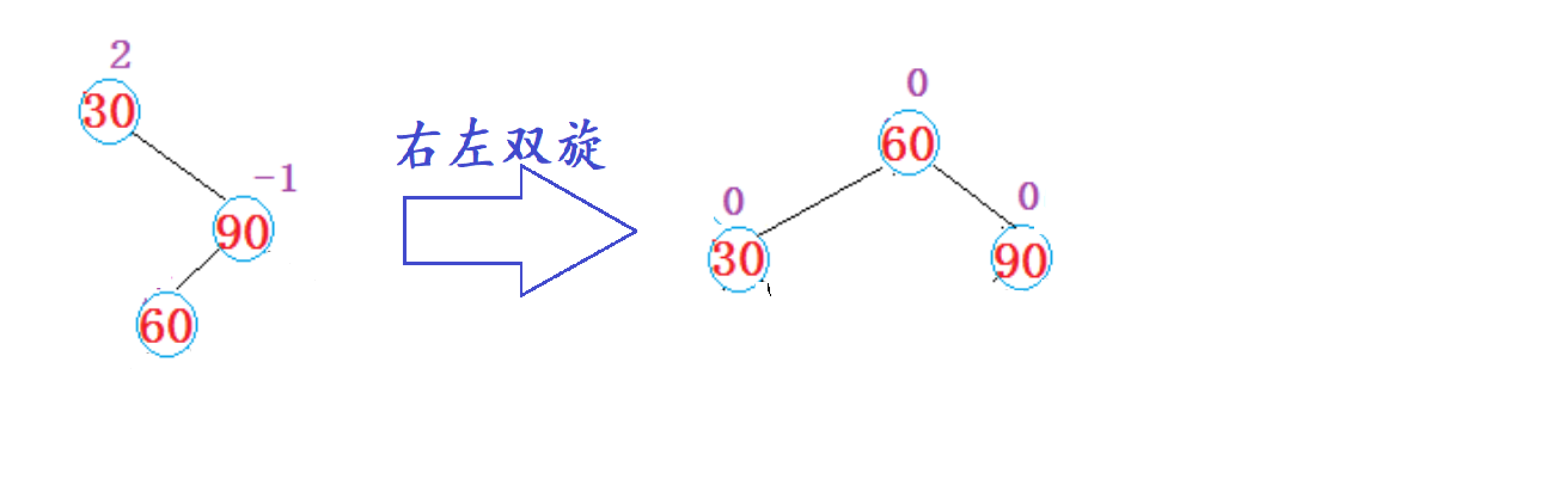
2. 如果单纯的对根节点进行左单旋，并不能解决右边高的问题，会变成左边高，所以要进行双旋，步骤如下：

1. 先对subR节点进行右单旋

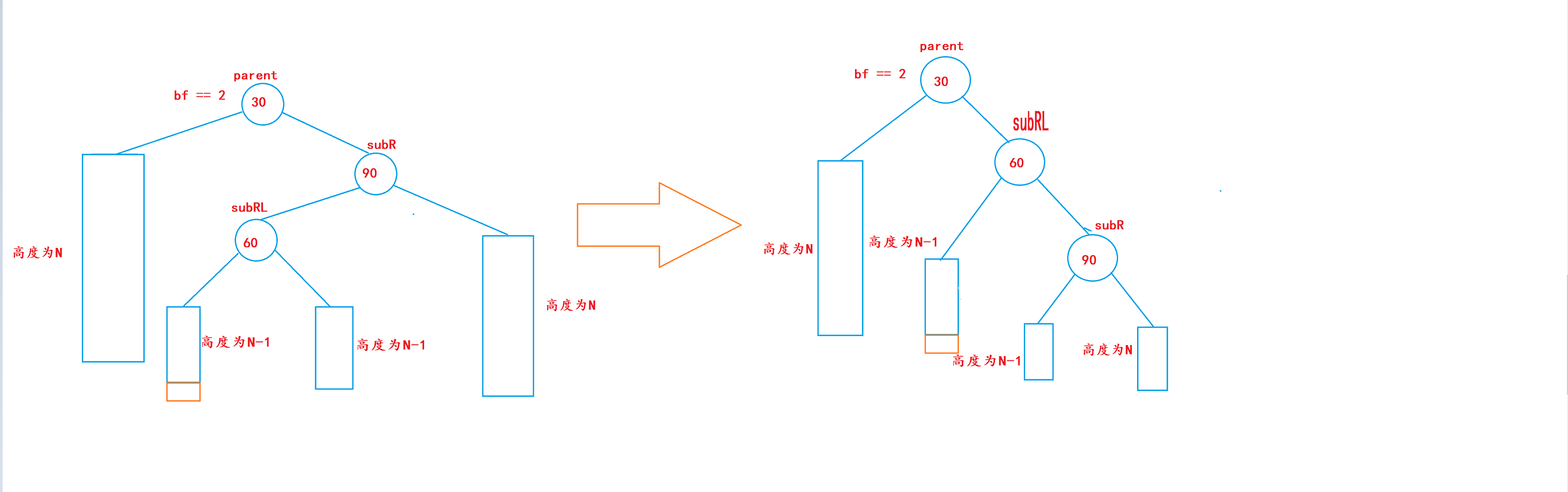
2. 对parent节点进行左单旋

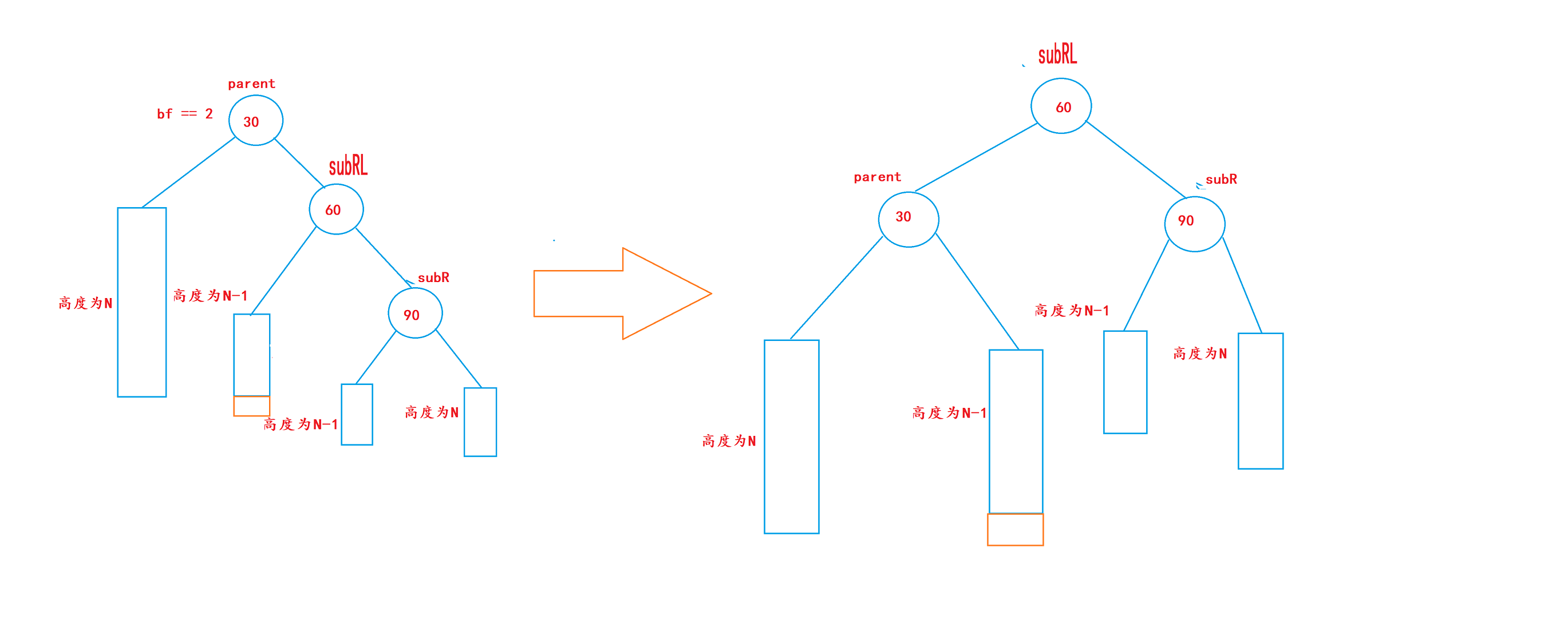
3. 完整步骤

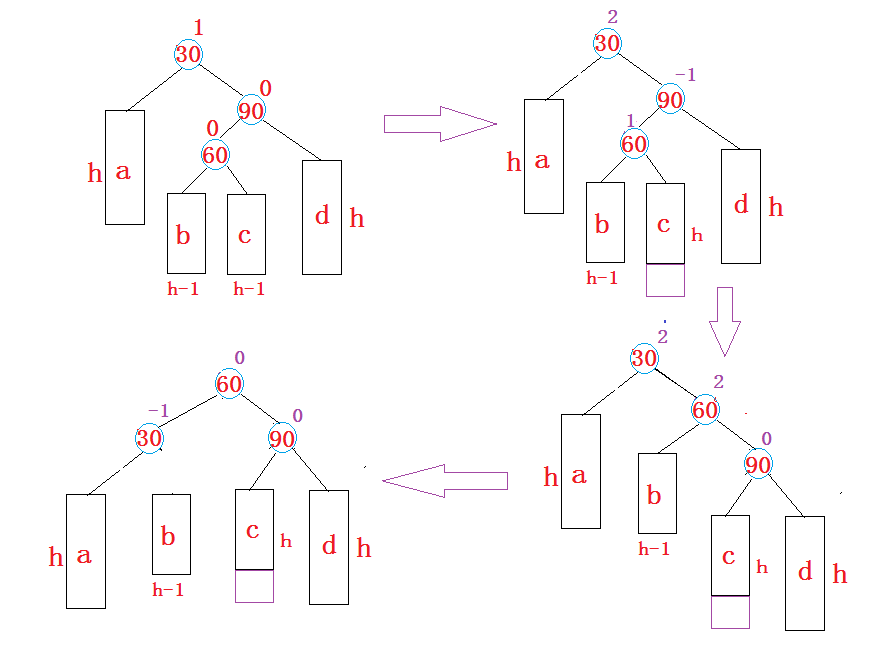
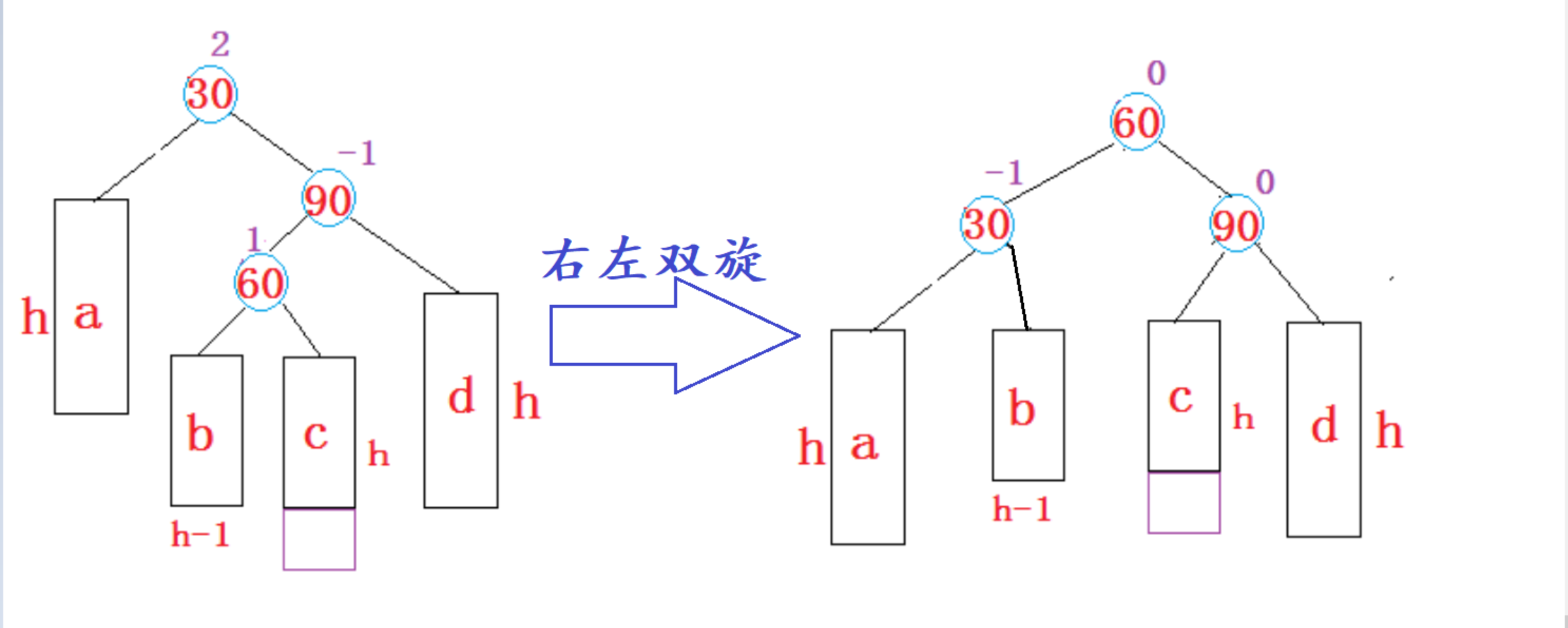
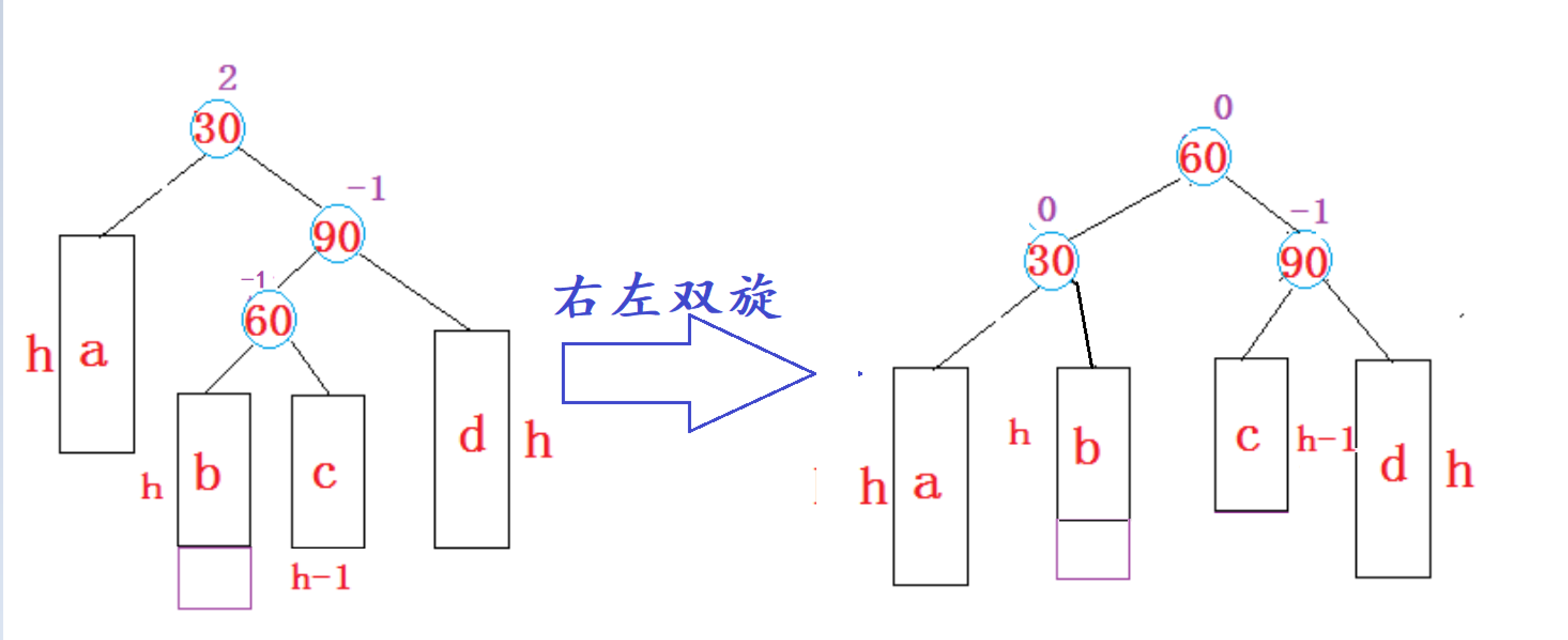
右左双旋后满足二叉搜索树的性质：

右左双旋后，实际上就是让subRL的左子树和右子树，分别作为parent和subR的右子树和左子树，再让parent和subR分别作为subRL的左右子树，最后让subRL作为整个子树的根。

1、subRL的左子树当中的结点本身就比parent的值大，因此可以作为parent的右子树。

2、subRL的右子树当中的结点本身就比subR的值小，因此可以作为subR的左子树。

3、经过步骤1、2后，parent及其子树当中结点的值都就比subRL的值小，而subR及其子树当中结点的值都就比subRL的值大，因此它们可以分别作为subRL的左右子树。

右左双旋后，平衡因子的更新随着subRL原始平衡因子的不同分为以下三种情况：

1、当subRL原始平衡因子是1时，右左双旋后parent、subR、subRL的平衡因子分别更新为-1、0、0。

2、 当subRL原始平衡因子是-1时，右左双旋后parent、subR、subRL的平衡因子分别更新为0、1、0

3、当subRL原始平衡因子是0时，左右双旋后parent、subR、subRL的平衡因子分别更新为0、0、0。

代码如下：

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1){subR->_bf == 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = parent->_bf = subRL->_bf = 0;}else {assert(false);}
}

---

3. AVL的验证

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

1. 验证其为二叉搜索树
   • 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树
2. 验证其为平衡树
   • 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
   • 节点的平衡因子是否计算正确

详解代码：

public:void InOrder()
{_InOrder(_root);
}int Size()
{_Size(_root);
}int Height()
{_Height(_root);
}bool IsBalanceTree()
{return _IsBalanceTree(_root);
}private:bool _IsBalanceTree(Node* root)
{if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);// 计算左右子树高度差绝对值int dec = abs(leftHeight - rightHeight);// 如果比1大说明不平衡if (dec > 1){cout << root->_kv.first << endl;return false;}// 检查平衡因子是否计算正确if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
int _Height(Node* root)
{if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return max(leftHeight, rightHeight) + 1;
}int _Size(Node* root)
{if (root == nullptr){return 0;}return _Size(root->_left) + _Size(root->_right) + 1;
}void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}

---

3. AVL的验证

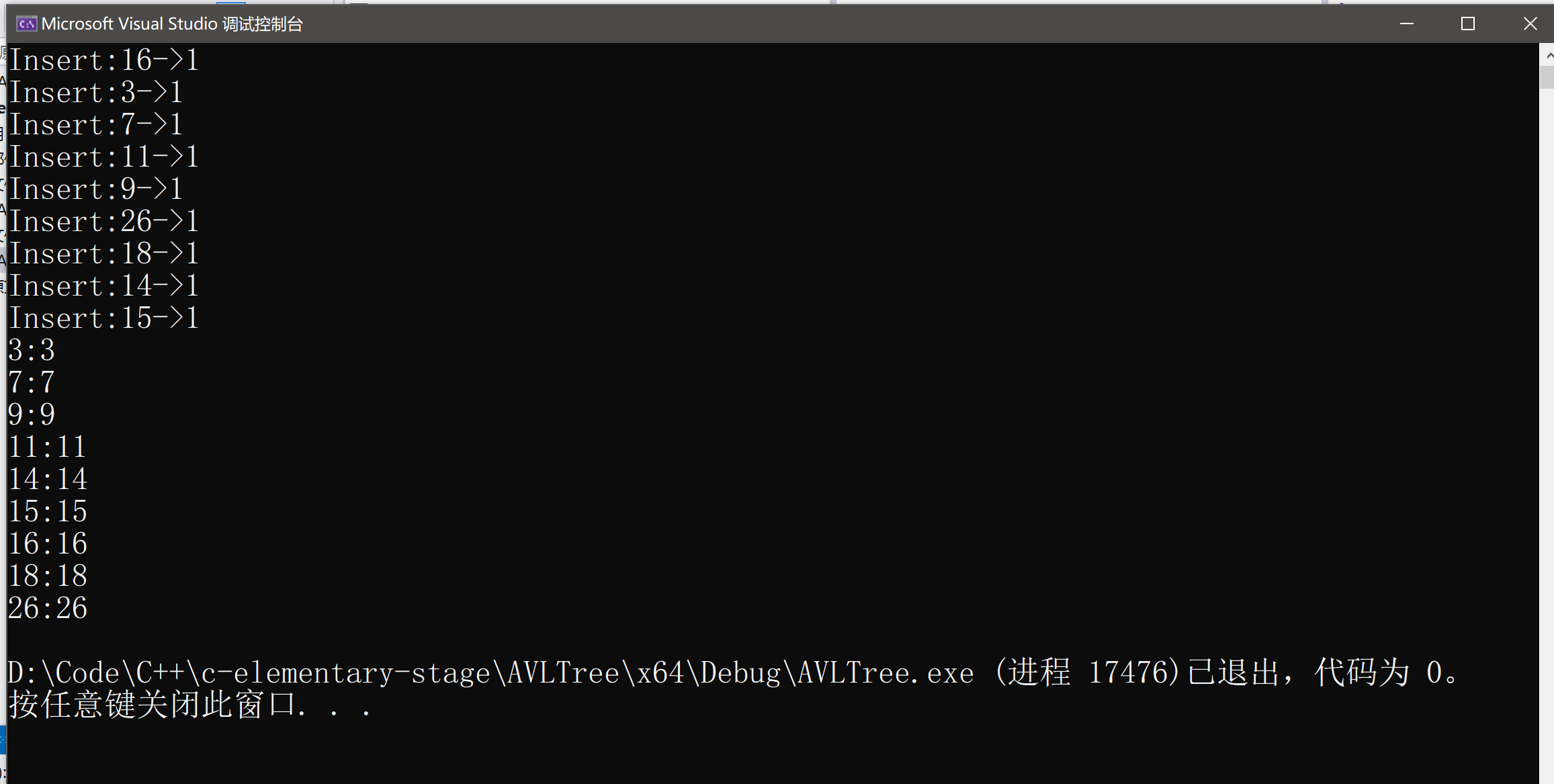
⚡验证示例1

int a[] = {16, 3, 7, 11, 9, 26, 18, 14, 15};

验证代码：

void AVLTest1()
{AVLTree<int, int> t;int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };for (auto& e : a){t.Insert({ e,e });cout << "Insert:" << e << "->" << t.IsBalanceTree() << endl;}t.InOrder();
}

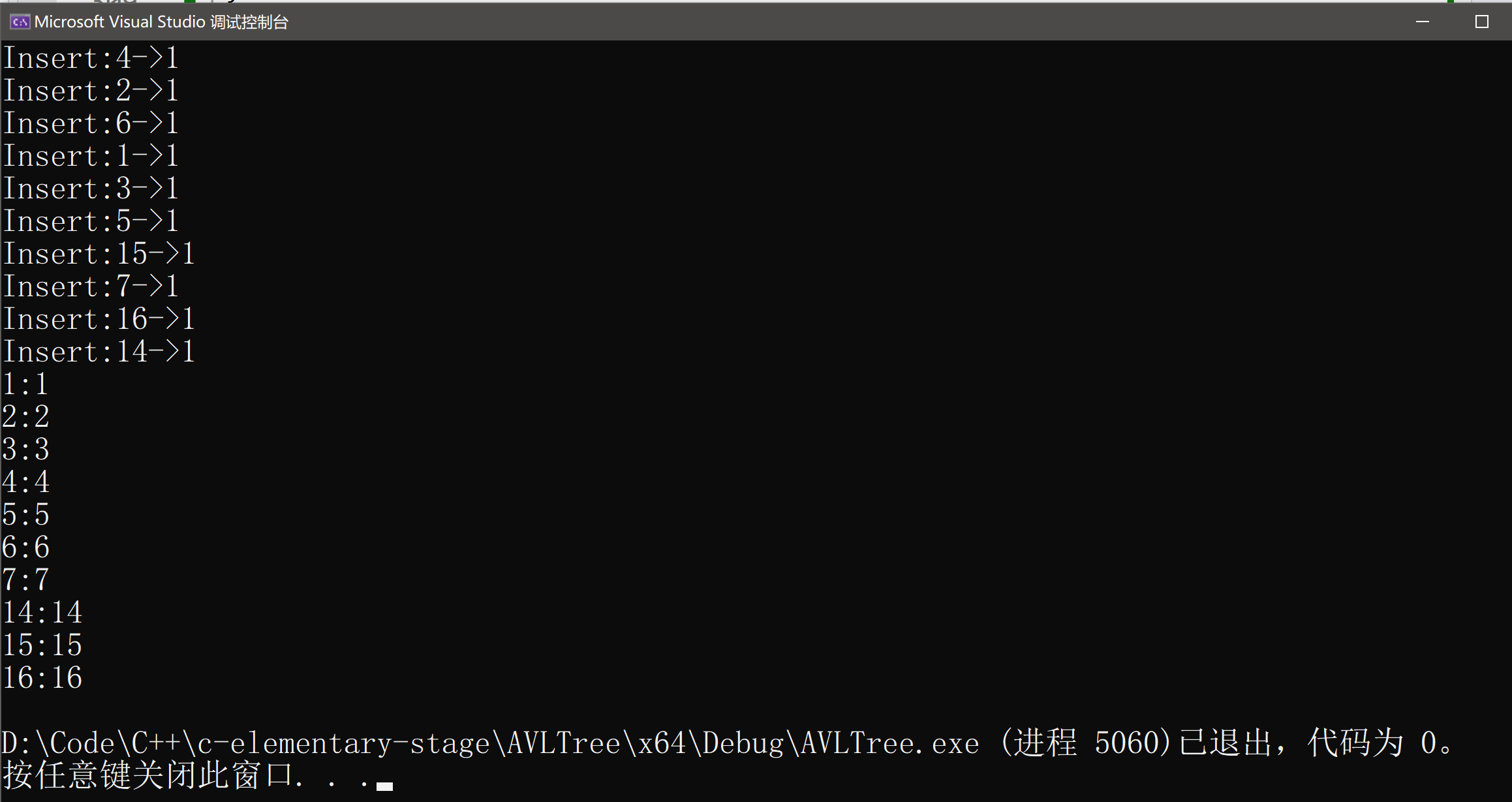
⚡验证示例2

int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };

验证代码：

void AVLTest1()
{AVLTree<int, int> t;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto& e : a){t.Insert({ e,e });cout << "Insert:" << e << "->" << t.IsBalanceTree() << endl;}t.InOrder();
}

---

3. AVL的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即$lo{g}_2(N)$。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。