目录

1. 感知机介绍

1.1 背景

1.2 定义

1.2.1 权重

1.2.2 阈值

1.2.3 偏置

1.3 逻辑处理：与门、非门、或门

2. 感知机实现

2.1 与门的 Python 实现

2.2 非门的 Python 实现

2.3 或门的 Python 实现

---

1. 感知机介绍

1.1 背景

        感知机1957年由 Rosenblatt 提出，是神经网络与支持向量机的基础。它是最简单最基础的机器学习算法，可以用于处理最简单的二分类任务，并且模型和学习算法都十分简单。

1.2 定义

        感知机是具有输入和输出的算法。给定一个或者输入之后，将输出一个既定的值。

        感知机接收多个输入信号，输出一个信号。输入信号可以用 0 或者 1 表示，0 表示 “不传递信号”，1 表示 “传递信号”。从多个输入信号到一个输出信号，即感知机算法。

        最简单的感知机算法可以理解为 1 个输入信号 x，输出 y；算法即 y = x

1.2.1 权重

        前面说了，感知机能接收多个输入信号，但是多个输入信号在感知机那边的权重可能是不一样的，即同样的信号传到感知机，感知机处理的是不一样的。

        比如有 x1,x2 两个信号，则有对应的权重 w1,w2。

        y= w1 * x1+w2 * x2

1.2.2 阈值

        1.2.1 说了加上权重之后的感知机算法 “y= w1 * x1+w2 * x2”，事实上感知机并非简单的将输入信号合并，它绝大多数时候是按照阈值来输出 0 或 1 这个信号的。

        假设存在一个阈值 θ，那么

                        y={0 (w1 * x1+w2 * x2 ≤ θ)

                             1 (w1 * x1+w2 * x2 ​> θ)​

1.2.3 偏置

        事实上上述加了阈值的算法，还可以理解为如下表达方式，其中 b 即 - θ

                        y={0 ( w1 * x1+w2 * x2 +b ≤ 0)

                             1 ( w1 * x1+w2 * x2 ​+b > 0)​

        这时候 b 可以称之为偏置。

1.3 逻辑处理：与门、与非门、或门

        相信大家都熟悉编程语言中的与、非、或三种最基本的逻辑关系，此处就不再赘述。感知机也可以用来处理这三种逻辑关系。

        与门：具有两个输入和一个输出的门电路，仅在两个输入信号都为 1 时候输出 1，其他输出 0

        与非门：即颠倒了与门的输出

        或门：只要两个输入信号有一个为 1,输出即为 1，其他输出 0

与门、与非门、或门的真值表达式

	输入信号		输出信号 y
	x1	x2	与门	与非门	或门
1	0	0	0	1	0
2	1	0	0	1	1
3	0	1	0	1	1
4	1	1	1	0	1

2. 感知机实现

2.1 与门的 Python 实现

        下面是与门的 Python 实现。权重分别是 w1 0.1、w2 0.2；阈值即 0.7。

def AND(x1,x2):w1,w2,theta = 0.1,0.2,0.7tmp=w1*x1+w2*x2if(tmp<=theta):return(0)else:return(1)
print(AND(0,0))
print(AND(0,2))
print(AND(0,4))
print(AND(1,3))
print(AND(2,4))
print(AND(5,0))
print(AND(7,0))

 结果显示程序正确

2.2 非门的 Python 实现

        下面是非门的 Python 实现。权重分别是 w1 0.1、w2 0.2；偏置即 -0.7。

def NAND(x1,x2):w1,w2 = -0.1,-0.2w=np.array([w1,w2]) # 权重转换成 array 方便计算x=np.array([x1,x2]) # 输入信号转换成 array 方便计算b=0.7 #设置偏置tmp=np.sum(w*x)+bif(tmp<=0):return(0)else:return(1)
print(NAND(0,0))
print(NAND(0,2))
print(NAND(0,4))
print(NAND(1,3))
print(NAND(2,4))

结果显示程序正确

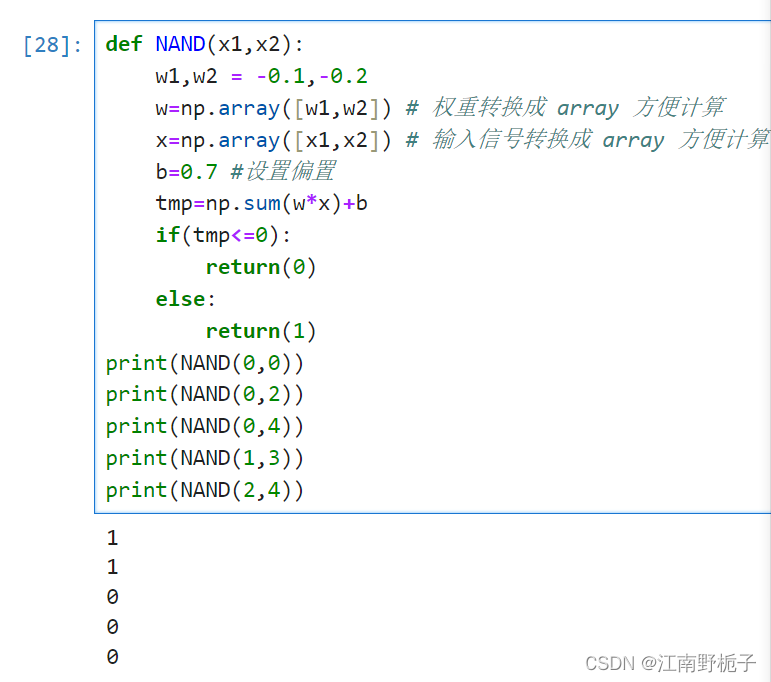
2.3 或门的 Python 实现

        或门的 Python 实现请大家自行实现，也许眼尖的同学已经发现了，与门、非门本质上代码是一致的，区别只是权重和偏置的值是正或者负了。

        代码实现

def  OR(x1,x2):w1,w2 = 0.1,0.2w=np.array([w1,w2]) # 权重转换成 array 方便计算，权重和 AND 不同x=np.array([x1,x2]) # 输入信号转换成 array 方便计算b=-0.7 #设置偏置，偏置和 AND 不同tmp=np.sum(w*x)+bif(tmp<=0):return(0)else:return(1)
print(OR(0,0))
print(OR(0,2))
print(OR(0,4))
print(OR(1,3))
print(OR(2,4))

'''

要是大家觉得写得还行，麻烦点个赞或者收藏吧，想给博客涨涨人气，非常感谢！

'''