目录
一:选择排序——原理
二:选择排序——分析
三:选择排序——实现
四:选择排序——优化
五:选择排序——效率
一:选择排序——原理
选择排序的原理:通过遍历数组,选出该数组中较大的或者较小的,放在数组的起始位置,当遍历完整个数组时排序完成。
二:选择排序——分析
选择排序的核心就是:多趟选择
若以升序(从小到大)排序为例,假若有N个数。
- 第一趟遍历的目的是找到整个序列中最小的值,找到之后将其与第一个数(动图中的第0个位置)交换,这样一来,在整个数组中第一个数就是最小的。
- 第二趟遍历:目的是找到整个序列中次小的值,也就是(动图中第0个位置上的数不在变动,在剩下的 N-1 个数中选出最小的),找到之后将其与剩下的 N-1 个数的第一个数(动图中的第1个位置)交换,这样一来,在整个数组中第一个数(第0位置)就是最小的,第二个数(第1位置)就是次小的。
- ......
当经过 N-1 趟的遍历交换之后,该序列就实现的从小到大的排列了。
动图如下: 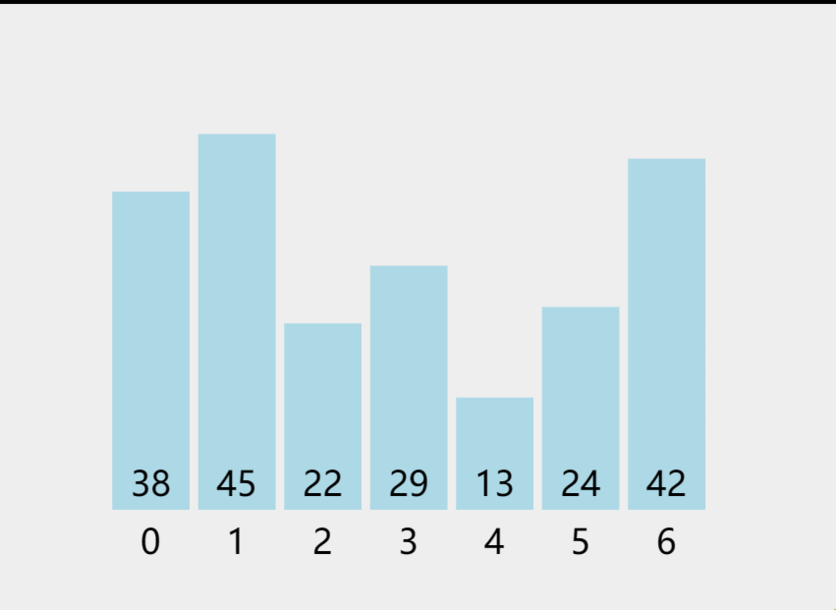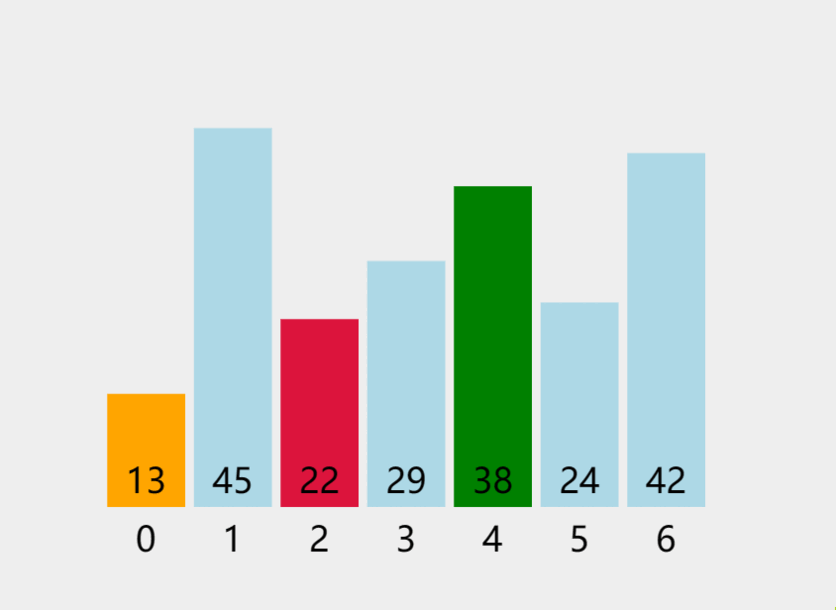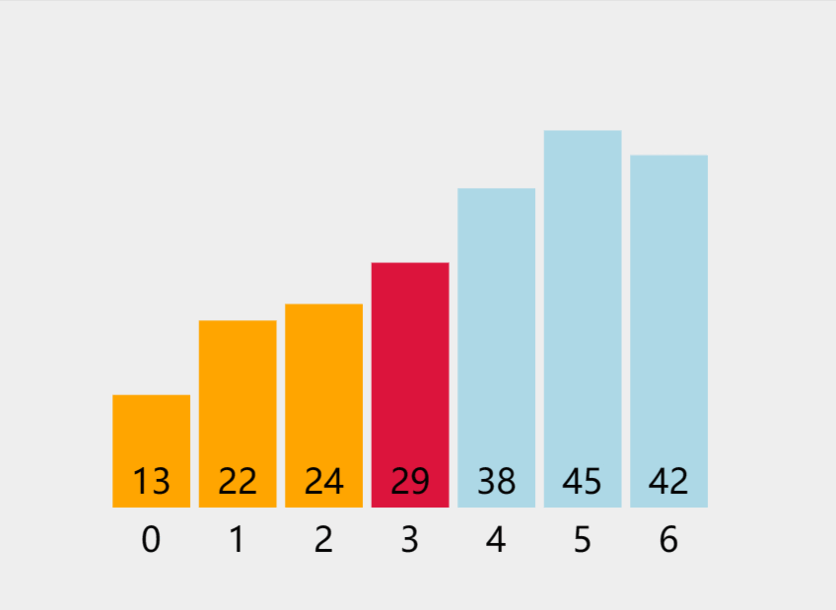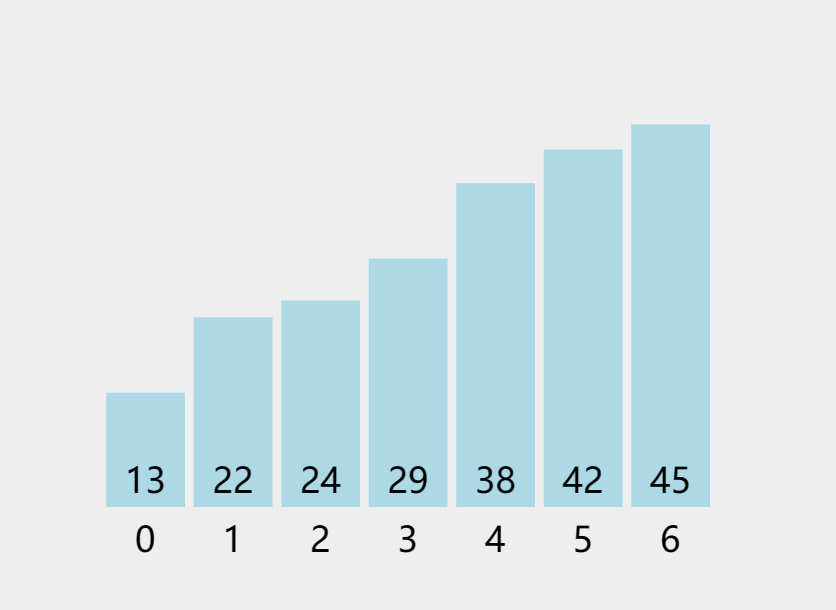
三:选择排序——实现
选择排序代码实现如下
#include<stdio.h>void SelectSort1(int* a, int n) // 传的参数是 整个数组 和 此数组的大小
{int begin = 0;while (begin < n) // 决定所遍历的趟数{int mini = begin;for (int i = begin; i < n; i++) // 从begin位置开始遍历{if (a[mini] > a[i]) // 找到较小的值,标记一下{mini = i;}}// 交换较小的值 // 遍历一趟之后,将较小的值与 ”第一个数“ 进行交换int tem = a[mini];a[mini] = a[begin];a[begin] = tem;begin++; // 决定下一次所遍历的起始位置:(第一趟是0,第二趟为1,....)}
}int main()
{int a[] = { 38,45,22,29,13,24,42 };int sz = sizeof(a) / sizeof(a[0]); // 获取数组大小for (int i = 0; i < n; i++) // 打印排序前的数组{printf("%d ", a[i]);}printf("\n");SelectSort1(a, sz); // 实现选择排序for (int i = 0; i < n; i++) // 打印排序后的数组{printf("%d ", a[i]);}printf("\n");
}
四:选择排序——优化
在选择排序中,我们是可以将其优化的,即可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
选择排序代码优化实现如下
#include<stdio.h>// 选择排序(优化)
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1; // begin标记第0位置,end标记最后一个数的位置while (begin < end) // 决定所遍历的次数{int maxi = begin; // 较大数---maxi变量标记int mini = begin; // 较小数---mini变量标记for (int i = begin; i <= end; i++) // 在 [begin,end] 这一区间进行遍历{if (a[i] > a[maxi]) // 遍历的数较大,maxi进行标记{maxi = i;}if (a[i] < a[mini]) // 遍历的数较小,mini进行标记{mini = i;}}Swap(&a[begin], &a[mini]); // 较小的数与 ”第一个数“ 交换,把较小的数放到 ”第一个位置“if (begin == maxi) // 若 ”第一个位置“ 是较大数的位置,防止这个位置被上一个交换所 ”赶跑“{maxi = mini;}Swap(&a[end], &a[maxi]); // 较大的数与 ”最后一个数“ 交换,把较大的数放到 ”最后一个位置“ 上++begin; // 决定下一次遍历的区间--end;}}int main()
{int a[] = { 38,45,22,29,13,24,42 };int sz = sizeof(a) / sizeof(a[0]); // 获取数组大小for (int i = 0; i < n; i++) // 打印排序前的数组{printf("%d ", a[i]);}printf("\n");SelectSort(a, sz); // 实现选择排序for (int i = 0; i < n; i++) // 打印排序后的数组{printf("%d ", a[i]);}printf("\n");
}时刻谨记:当一个数已经知道其是 最大/最小 ,并已经将其进行交换之后,那么这个位置是万万不可变动的。
五:选择排序——效率
时间复杂度:O(N^2)
空间复杂度:O(1)
选择排序是不稳定的排序。
选择排序是最简单的排序之一,最大的优点就是好理解,不过因为其效率低下,所以在一般情况下不使用。
以上的内容若是对大家起到帮助的话,大家可以动动小手点赞,评论+收藏。大家的支持就是我进步路上的最大动力!