优质博文：IT-BLOG-CN

一、题目

给你一个整数数组nums，返回数组answer，其中answer[i]等于nums中除nums[i]之外其余各元素的乘积。题目数据保证数组nums之中任意元素的全部前缀元素和后缀的乘积都在32位整数范围内。请不要使用除法，且在O(n)时间复杂度内完成此题。

示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证数组nums之中任意元素的全部前缀元素和后缀的乘积都在32位整数范围内

进阶：你可以在O(1)的额外空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组 不被视为 额外空间。）

二、代码

【1】创建左右乘积列表： 我们不能将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。初始化两个数组Left和Right，对于指定的下表i，left[i]代表i左侧所有数据的乘积，right[i]代表i右侧所有数据的乘积。我们利用循环将数据填充到lfet[]和right[]数组中，然后将left[i]和right[i]相乘就是i的左右乘积。

class Solution {public int[] productExceptSelf(int[] nums) {if (nums == null || nums.length == 0) {return null;}// 我们使用数组，也就是当前数字的left[] 和 right[] 数组，分别存储左右两边的和;int len = nums.length;int res[] = new int[len];int left[] = new int[len];int right[] = new int[len];// 第一个数之前的数的乘积为1，所以先给个默认值left[0] = 1;for (int i = 1; i < len; i++) {// left 中保存的是i之前所有数的乘积left[i] = left[i - 1] * nums[i - 1];}// 最有边的数也保存为1right[len - 1] = 1;for (int i = len - 2; i >= 0; i--) {right[i] = right[i + 1] * nums[i + 1];}for (int i = 0; i < len; i++) {res[i] = left[i] * right[i];}return res;}
}

时间复杂度： O(N)，其中N指的是数组nums的大小。预处理L和R数组以及最后的遍历计算都是O(N)的时间复杂度。
空间复杂度： O(N)，其中N指的是数组nums的大小。使用了L和R数组去构造答案，L和R数组的长度为数组nums的大小。

【2】空间复杂度O(1)的方法： 由于输出数组不算在空间复杂度内，那么我们可以将L或R数组用输出数组来计算。先把输出数组当作L数组来计算，然后再动态构造R数组得到结果。

class Solution {public int[] productExceptSelf(int[] nums) {if (nums == null || nums.length == 0) {return null;}// 因为返回的数组可以不算在空间复杂度中，所以可以作为临时变量存放left[]数据int len = nums.length;int res[] = new int[len];// // 第一个数之前的数的乘积为1，所以先给个默认值res[0] = 1;for (int i = 1; i < len; i++) {// left 中保存的是i之前所有数的乘积res[i] = res[i - 1] * nums[i - 1];}// 然后从后向前变量，通过变量 right保存前几位数的乘积int right = 1;for (int i = len - 1; i >= 0; i--) {res[i] *= right;// 放在返回值的后面，就相当于i + 1right *= nums[i];} return res;}
}

时间复杂度： O(N)，其中N指的是数组nums的大小。分析与方法一相同。
空间复杂度： O(1)，输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。

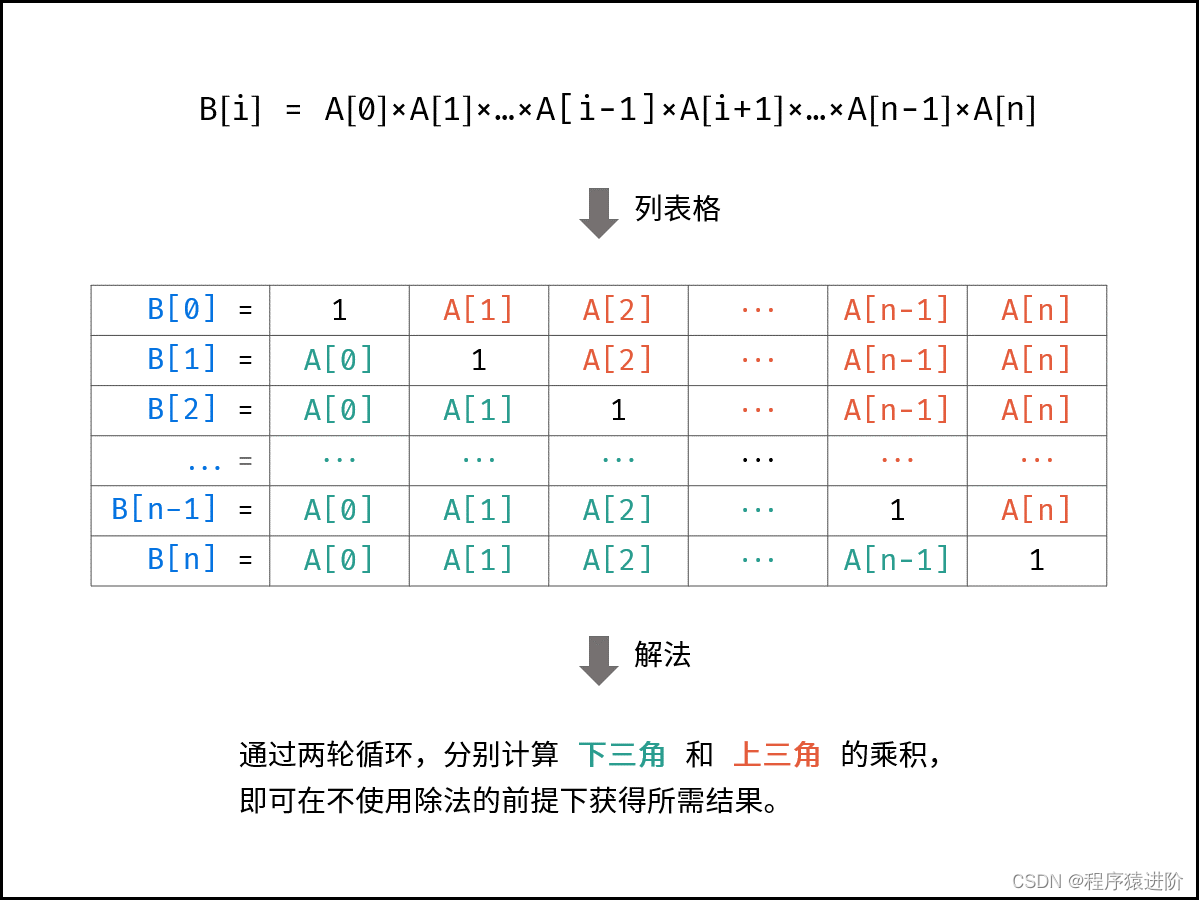
【3】本题的难点在于不能使用除法 ，即需要只用乘法生成数组 ans。根据题目对ans[i]的定义，可列出下图所示的表格。

根据表格的主对角线（全为1），可将表格分为上三角和下三角两部分。分别迭代计算下三角和上三角两部分的乘积，即可 不使用除法 就获得结果。

下图中A=nums, B=ans

算法流程：
初始化： 数组ans，其中ans[0]=1；辅助变量tmp=1。
计算ans[i]的下三角各元素的乘积，直接乘入ans[i]。
计算ans[i]的上三角各元素的乘积，记为tmp，并乘入ans[i]。
返回ans。

class Solution {//假如nums为[1,2,3,4]，那么answer的值分别为[(2,3,4),(1,3,4),(1,2,4),(1,2,3)]//如果吧i当前值相乘的时候看做是1那么就有如下样式//  1, 2, 3, 4 //  1, 1, 3, 4//  1, 2, 1, 4//  1, 2, 3, 1// 他的对角线1将他们分割成了两个三角形，对于answer的元素，//我们可以先计算一个三角形每行的乘积，然后再去计算另外一个三角形每行的乘积，//然后各行相乘，就是answer每个对应的元素public int[] productExceptSelf(int[] nums) {int length = nums.length;//先初始化一个answer数组,但是很多解答都没说明的是这个answer数组，//并不是以此计算就得出的结果,而是两次乘积之后的结果int[] answer = new int[length];//初始化一个初始值，作为三角乘积计算的开始answer[0] = 1;//先计算左边三角的乘积for(int i = 1; i < length; i++){answer[i] = answer[i-1] * nums[i-1];}//再次计算右边三角形,为什么是length-2呢？//length-1是最后一个值的索引，但是最后一个值temp[length-1] = 1,//也是对应对角线上的1，所以不在进行相乘处理//temp的作用是计算右边三角形的乘积的累计值，然后再和answer相乘，//注意!!!:不能直接nums[i+1]相乘那会在计算右三角的时候变成每行乘积与nums[i+1]的错误答案int temp = 1;for(int i = length - 2; i >= 0; i--){//先将每行乘积赋予一个中间值temp *= nums[i+1];answer[i] *= temp;}return answer;}
}

时间复杂度O(N) ： 其中N为数组长度，两轮遍历数组nums，使用 O(N)时间。
空间复杂度O(1) ： 变量tmp使用常数大小额外空间（数组ans作为返回值，不计入复杂度考虑）。

原数组：       [1       2       3       4]
左部分的乘积：   1       1      1*2    1*2*3
右部分的乘积： 2*3*4    3*4      4      1
结果：        1*2*3*4  1*3*4   1*2*4  1*2*3*1

从上面的图可以看出，当前位置的结果就是它左部分的乘积再乘以它右部分的乘积。因此需要进行两次遍历，第一次遍历用于求左部分的乘积，第二次遍历在求右部分的乘积的同时，再将最后的计算结果一起求出来。

【4】不准用除法，那我就用右移运算。先求出整个数组的乘积。然后利用极限的思想，用右移运算符，配合加法累算，得出总乘积是数组中每个元素的倍数。

咱们不用除法，但是需要用一点微积分知识。

class Solution {
public:int compute(int sum,int val){if(val==1) return sum;int k=0,cnt;long long tmp; while(sum>0){cnt=0;tmp=val;while(tmp<<1<sum){cnt++;tmp<<=1;}sum-=tmp;k+=1<<cnt;}return k;}vector<int> productExceptSelf(vector<int>& nums){int n=nums.size(),k;int idx=1,cnt=0;int sum,val;for(auto v:nums){if(v==0){cnt++;if(cnt==2) break;}else idx*=v;}if(cnt>0){for(auto& v:nums){if(cnt==1&&v==0)v=idx;else v=0;}return nums;}for(auto& v:nums){sum=abs(idx);val=abs(v);k=compute(sum,val);if(idx<0&&v<0||idx>0&&v>0)v=k;else v=k*-1;}return nums;}
};