文章目录
- 关于二叉树的创建
- 如何创建二叉树
- 实现二叉树的前、中、后序遍历
- 层序遍历
关于二叉树的创建
在笔者的上一篇文章中堆进行了一个详细介绍,而二叉树是以堆为基础进行创建,它与堆的显著不同是
堆像是一个线性结构,堆的结构往往是一个数组,通过对父子索引的查找进行大多数功能的实现
而二叉树是一个逻辑结构,通过结构体实现二叉树的每一个节点,然后再通过指针将各个节点给联系起来
这里放一下两者的结构体对比,更加明显些
- 堆
typedef int QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
- 二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(int x);
如何创建二叉树
如果需要创建一个二叉树,我们往往需要一个能够提供二叉树元素根前序逻辑的数组,比如这个
char a[17] = { ‘A’,‘B’,‘D’,‘#’,‘#’,‘E’,‘#’,‘H’,‘#’,‘#’,‘C’,‘F’,‘#’,‘#’,‘G’,‘#’,‘#’ };
这里补充一下前序、中序、后序的概念
- 前序遍历(Preorder Traversal 亦称先序遍历)–访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)–访问根结点的操作发生在遍历其左右子树之中(间)
- 后序遍历(Postorder Traversal)–访问根结点的操作发生在遍历其左右子树之后。
比如说前序:即根-左孩子-右孩子的顺序呈现二叉树的逻辑
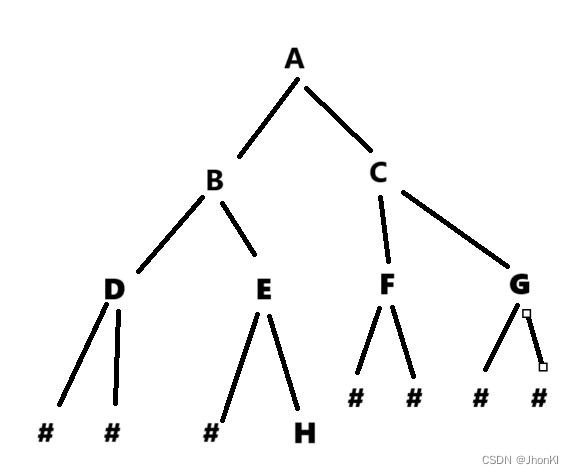
既然能理解前序的概念我们就可以发现如果暗战数组元素顺序,那么第一个进来的就是根,通过递归本函数,我们可以实现先将根创建完后再创建左子树,最后创建右子树
一旦遇到 # 我们就退出递归,回到上一级
还需要注意的是,我们用来创建二叉树的往往是一个堆逻辑的数组,所以为了获取下一个元素,我们需要一个能够在递归时确定当前元素下标的变量,因此我们可以这样子做
int b = 0;int* pi = &b;
由此一来pi对应是b的指针,即使在递归途中,我们不用改变指针pi直接通过指针改变b的值,即可以实现定位元素下标了
实现代码如下
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return;}node->data = x;node->left = NULL;node->right = NULL;return node;
}// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{//a为外界传进的数组//n为最大长度//pi为我们遍历数组的指针//使用‘#’表示NULL//(*pi)++ 意味着pi所指向的那个数加一,所以pi作为指针,它所指向的数的地址不会发生变化,但它所指向的那个数会加一if (a[*pi] == '#' || *pi >= n){printf("N ");(*pi)++;//因为是二叉树,所以遇到 '#' 意味着后面很有可能还有,所以pi所指向的那个数,即要查看现在查看的数组元素的下一个元素return NULL;}//若不为#就要创建一个新的节点BTNode* dst = BuyNode(a[(*pi)]);printf("%c ", dst->data);//递归数组的下一个元素(*pi)++;//赋值左右节点元素给当前节点dst->left = BinaryTreeCreate(a, n, pi);dst->right = BinaryTreeCreate(a, n, pi);return dst;
}
另外加一嘴,因为我们创建的二叉树是一个一个节点创建的,所以我们为了避免内存泄漏,最后也是需要通过递归一个一个释放,这里我们可以通过函数递归一直找到叶子节点,往上一个一个释放,即
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{//利用二叉树节点的特点,递归到最底层的结点,并释放//再一层层返回调用,自下而上逐渐销毁if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);root = NULL;return;
}
实现二叉树的前、中、后序遍历
刚刚我们提到了前、中、后序的概念,所以当我们需要通过这三种形式提取二叉树中的元素,通过递归左右节点来获取根节点,就可以通过改变三者的输出顺序即可实现,还是比较简单的
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}
层序遍历
层序遍历就与之前的遍历不同了,因为父子节点中往往可以通过指针直接获取对应的额位置和值,但是同一层中的节点却无法通过这种方法实现。
因此,我们需要用到之前学的一个数组结构 - 队列,即先进先出的数据结构
通过这种数据结构,我们将每次提取出来的节点放到队列的末尾,这样最后输出的队列,从头往后就是二叉树的层序遍历。
需要注意的是,如果大家在看别的博客的时候可能会遇到,他们直接使用队列的尾插功能,但其实这病不行,因为队列我们在创建时它的尾插功能的对象往往是队列的结构体,如果直接将其用来放入二叉树的层序遍历功能中,会出现bug
因此我们在二叉树中新建一个队列尾插功能,并将其的形参设为二叉树的结构体
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{if (root == NULL) {return;}// 使用队列实现层序遍历int front = 0, rear = 0;BTNode** queue = (BTNode**)malloc(sizeof(BTNode*) * 1000); // 假设节点数不超过1000queue[rear++] = root;while (front < rear) {BTNode* current = queue[front++]; // 取出队列前端节点printf("%c ", current->data);if (current->left != NULL) {queue[rear++] = current->left; // 左子节点入队}if (current->right != NULL) {queue[rear++] = current->right; // 右子节点入队}}free(queue); // 释放队列内存
}
不仅如此,最后为了防止内存泄漏,我们需要把这个新建立的队列给释放,注意不能全部释放二叉树,要不然后面就没得用了