关键词:预测性维护、盲源分离、振动分析、传递函数移除、二阶循环平稳性、轴承监测、机器学习
振动是旋转机械中主要的故障指示器,它们主要来源于两个方面:一个是与齿轮相关的振动(主要源于齿轮啮合过程中的冲击和不平衡负载),另一个是与轴承故障相关的低能量信号(主要源于轴承内部或外部的故障)。这些信号在传输到传感器的过程中,都会被机械的传递函数扭曲。我们提出的方法能够实现振动源的盲分离,即不需要任何关于被监控设备或外部测量的信息。
这种方法分为两个阶段来估计两个信号源:首先,使用扩张卷积神经网络(dilated CNN)隔离齿轮信号,然后,使用残差信号的平方对数包络来估计轴承故障信号。通过基于白化的去卷积方法(WBD),可以从这两个信号源中移除传递函数的影响。无论是在模拟还是实验结果中,都证明了该方法能够在没有额外信息的情况下能及早检测到轴承故障。
1、总体流程
- 周期-随机分离(Periodic-stochastic separation, PSS): 使用膨胀卷积神经网络(dilated CNN)来分离信号中的周期分量和随机分量。
- 反卷积滤波器设计(Deconvolution filter design): 基于随机分量的相关性矩阵,使用白化反卷积(Whitening-based deconvolution, WBD)方法来设计反卷积滤波器。
- 反卷积(Deconvolution): 对周期分量和随机分量分别进行反卷积,以消除传递函数的影响。
- 统计假设检验(Statistical hypothesis testing): 对反卷积后的随机分量进行统计假设检验,以检测循环平稳分量,进而估计轴承故障信号。
2、技术参数微调适应不同场景
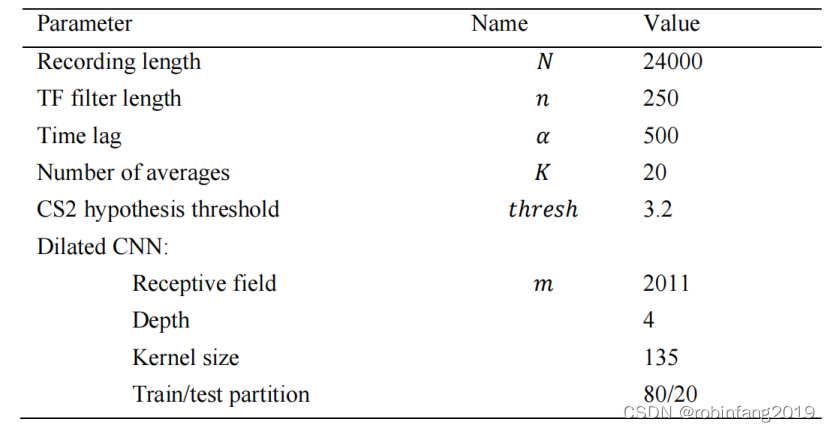
- 膨胀卷积神经网络参数:根据所需的频率分辨率,设置适当的感受野长度m(例如0.5秒对应2Hz分辨率)。同时,选择合适的模型深度(4层左右),以及内核大小(与m和模型深度相关)。
- 大时间滞后α:建议设置α≥n,以确保随机分量在时间滞后大于α时相关为零。
- 频域平均数K:用于估计CS2信号的方差,建议在20以下取值,以平衡阈值选择、计算复杂度和频率分辨率。
- CS2假设检验阈值:根据所需的显著性水平p选择,建议在0.001-0.01之间。
- 信号长度N:应足够长以包含多个循环周期,例如1秒对应24kHz采样频率。
- 稳定性检验:检查信号能量的稳定性,以确保在稳定条件下进行分析。
- 预处理:根据实际设备,可能需要添加预处理步骤,例如滤波以抑制非相关噪声。
- 模型训练:根据实际信号调整CNN模型的训练参数,例如批量大小、学习率等。
3、实际场景运用该方法面临的挑战
- 操作条件变化:实际操作条件下,旋转机械的转速和负载会频繁变化,而该方法是基于稳定操作条件设计的。因此,需要进一步研究以扩展该方法以适应变化的操作条件。
- 信号类型限制:该方法目前仅适用于特定类型的二阶循环平稳信号来模拟轴承故障。在实际应用中,信号可能存在差异,从而增加估计误差。
- 传递函数不可逆:假设传递函数是可逆的。如果不可逆,可能需要采用其他方法设计反卷积滤波器。
- 附加噪声问题:实际测量中可能存在额外的白噪声,这需要进一步的研究来解决。
- 验证信号稳定性:需要验证信号的稳定性,以确保在稳定的操作条件下进行。然而,这需要额外的信息,因此也是实际应用中的挑战之一。
- 故障类型区分:方法目前无法区分局部和分布式故障,因为两者在频谱中都有峰值。在实际应用中,这可能是一个问题。
- 运算复杂度:方法涉及较为复杂的运算,例如使用膨胀卷积神经网络进行信号分解,这可能限制其在计算资源有限的传感器上的应用。
4、相关名词
传递函数:传递函数在机械系统中的应用非常广泛,它是连接输入与输出之间关系的数学描述,可以用于分析系统的动态行为和稳定性。例如,在旋转机械中,通过对广义矢量方程应用拉普拉斯变换,可以轻松扩展传递函数的概念,从而精确定义瞬态和亚瞬态电抗以及时间常数等经典概念。
二阶循环平稳性(Second Order Cyclostationarity):指一个非平稳信号在时间域中存在某种周期性,使得其二阶统计特性(如功率谱密度、互相关函数等)具有周期性。这与传统的循环平稳性不同,后者通常关注一阶统计特性的周期性。