class Solution:def numSquares(self, n: int) -> int:dp=[i for i in range(n+1)]for i in range(2,n+1):for j in range(1,int(i**(0.5))+1):dp[i]=min(dp[i],dp[i-j*j]+1)return dp[-1]

代码解释

1. 初始化 DP 数组：
   dp = [i for i in range(n+1)]
   这里，dp[i] 表示数字 i 可以由多少个完全平方数组成。初始时，假设每个数字都由它本身一个完全平方数组成，即 dp[i] = i。
2. 动态规划：
   外层循环遍历从 2 到 n 的所有数字 i。
   内层循环遍历从 1 到 sqrt(i) 的所有整数 j。这里 j 是可能的完全平方数的平方根。
   对于每个 i 和 j，我们尝试将 i 分解为 j*j 和 i-j*j 两部分。如果 i-j*j 仍然是非负的，那么 dp[i] 可以更新为 dp[i-j*j] + 1（即 i-j*j 所需的完全平方数加上当前的 j*j）。
   但是，我们要确保 dp[i] 始终是最小的值，因此我们使用 min(dp[i], dp[i-j*j]+1) 来更新它。
3. 返回结果：
   最后，dp[-1] 就是 n 可以由的最少完全平方数之和，因为 dp 数组的下标是从 0 到 n 的。

举例

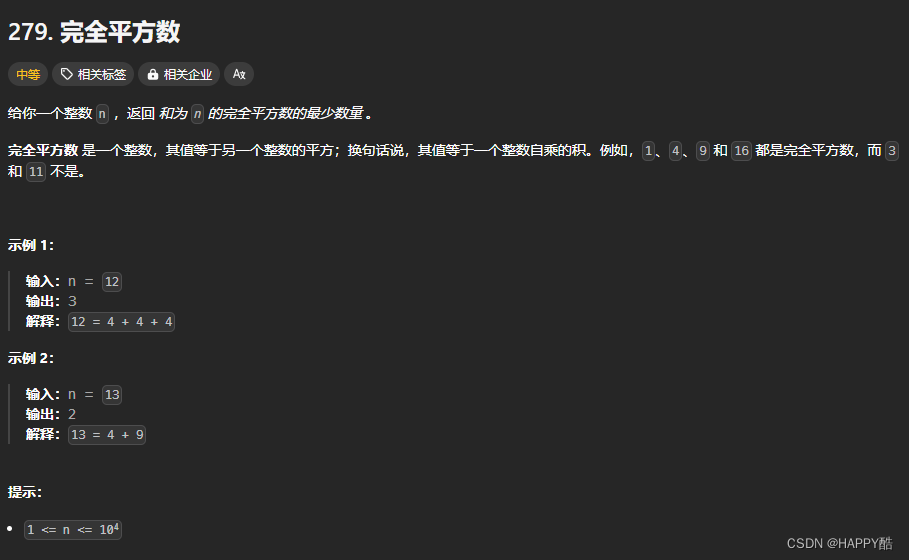
假设 n = 12。

初始时，dp 数组为：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

开始动态规划：

• 当 i = 2，j 可以是 1，因为 2 = 1*1 + 1*1（但这里我们只使用一个平方数），所以 dp[2] = 1
• 当 i = 3，j 只能是 1，因为 3 = 1*1 + 2，但 2 不是一个完全平方数，所以 dp[3] 保持为 3
• …
• 当 i = 4，j 可以是 1 或 2，因为 4 = 1*1 + 3 或 4 = 2*2，后者更优，所以 dp[4] = 1
• 当 i = 12，我们考虑所有可能的 j 值，并找到最佳组合。最终，12 = 4 + 4 + 4（或 12 = 1 + 3 + 8 等，但 4+4+4 是最少的），所以 dp[12] = 3

最终，dp[-1]（即 dp[12]）为 3，表示 12 可以由 3 个完全平方数组成。