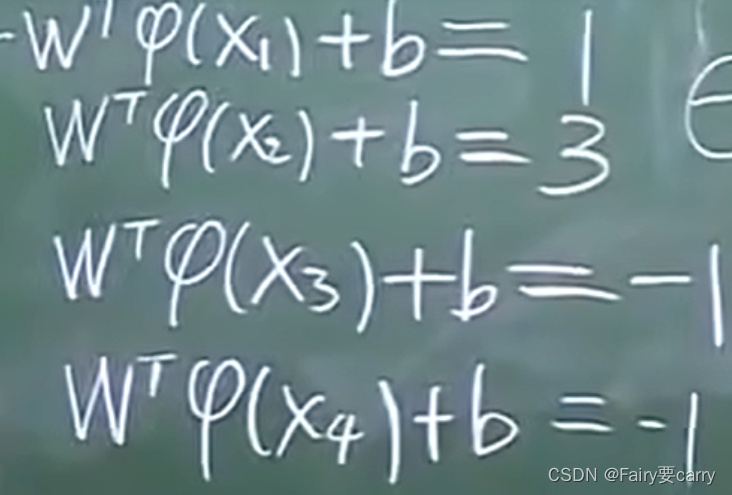这两周邻近毕业故没有很多时间来学习课余内容,另外最近身体有些不舒服【偏头痛】,所以学的内容不多,包括SVM向量机和ResNet【不包括代码复现】
1.SVM支持向量机的大概内容
1、目的:
- 主要内容是如何找到分类的那条线【超平面】——>此线应该是唯一的,那么如何保证两条平行线的最大距离d。
2.而我们的SVM的目的就是找到这个最大化d以及分类的超平面。
2、相关工作:
1.点到平面的距离【因为要寻找到我们对样本进行分类的超平面】——>进而衍生到了向量X0到超平面的距离。
2. 将距离公式进行演变 ,目的是最大化d即为最小化||w||^2。
**3.给模型规定限制条件:**目的是区分支持向量和非支持向量。
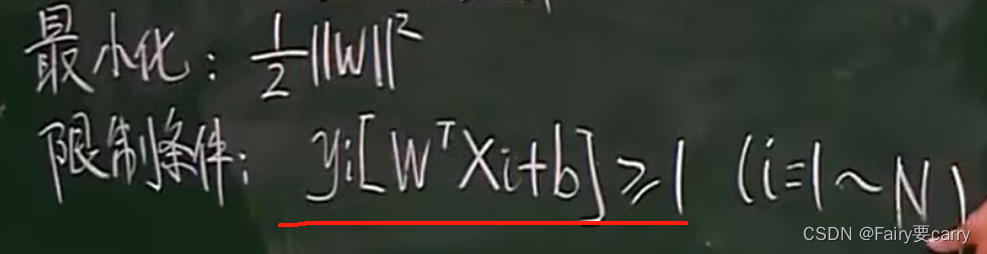
3.引入松弛变量求W: 但是最小化方程1/2||W||^2最小化求极值点W是无解的,所以我们需要添加一个正则项(Regulation Term)去求解【也就是我们的松弛变量,在反向传播算法中常用来减少梯度消失问题】,还有一种可能优化问题求解的解并不是我们想要的,我们也需要加一个正则项。【本质凸优化问题求唯一极值点】
4.问题:但是如果样本为线性不可分,则无法进行分类:
1、引入思想: 高维映射,将低维矢量映射到高维,然后用一个向量代数式表示。【这里用了异或问题进行解释,参考链接】
在这里也有一个思想出现了:无限维度被线性可分的概率接近1。2、后面得到了约束条件的方程【本质类似与低维,只是我们的W变成向量,而那个fai函数也是一个高维映射,两内积相乘为常量】,可以发现分类结果已经出来了。
5.所以按过程来说我们应该要求这个高维映射函数,这里涉及核函数的引入【具体推导过程参考链接】
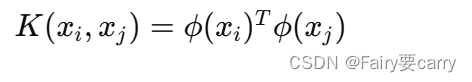
目的:无需显式的计算高维映射函数,内积得到常量,减少复杂性【推导过程极其优美】
6.引入对偶问题和原问题,将优化问题转换到对偶空间【引入拉格朗日乘数,主要好处是优化问题变成了仅依赖于数据点之间内积的形式,在后续公式推导中可以直接将核函数进行带入计算出高维空间的内积(核技巧)】
笔记一:
关于对偶问题的学习以及原问题如何转换为对偶问题的学习
笔记二:
SVM解决线性可分问题
2.ResNet残差网络的学习
、
本文基于何明凯前辈论文的学习,首先是学习了残差网络的背景,就于梯度消失和cnn参数过大FLOPs过多,以及VGG/plain网络的劣势进行对比,进而提出方案【所涉及的技术,如何改进等】
笔记三:
https://blog.csdn.net/weixin_57128596/article/details/139223695
3.写了一个关于阿里艺术字的接口:
基于WordArt锦书模型,输入字体和提示词即可生成关于提示词的艺术字。
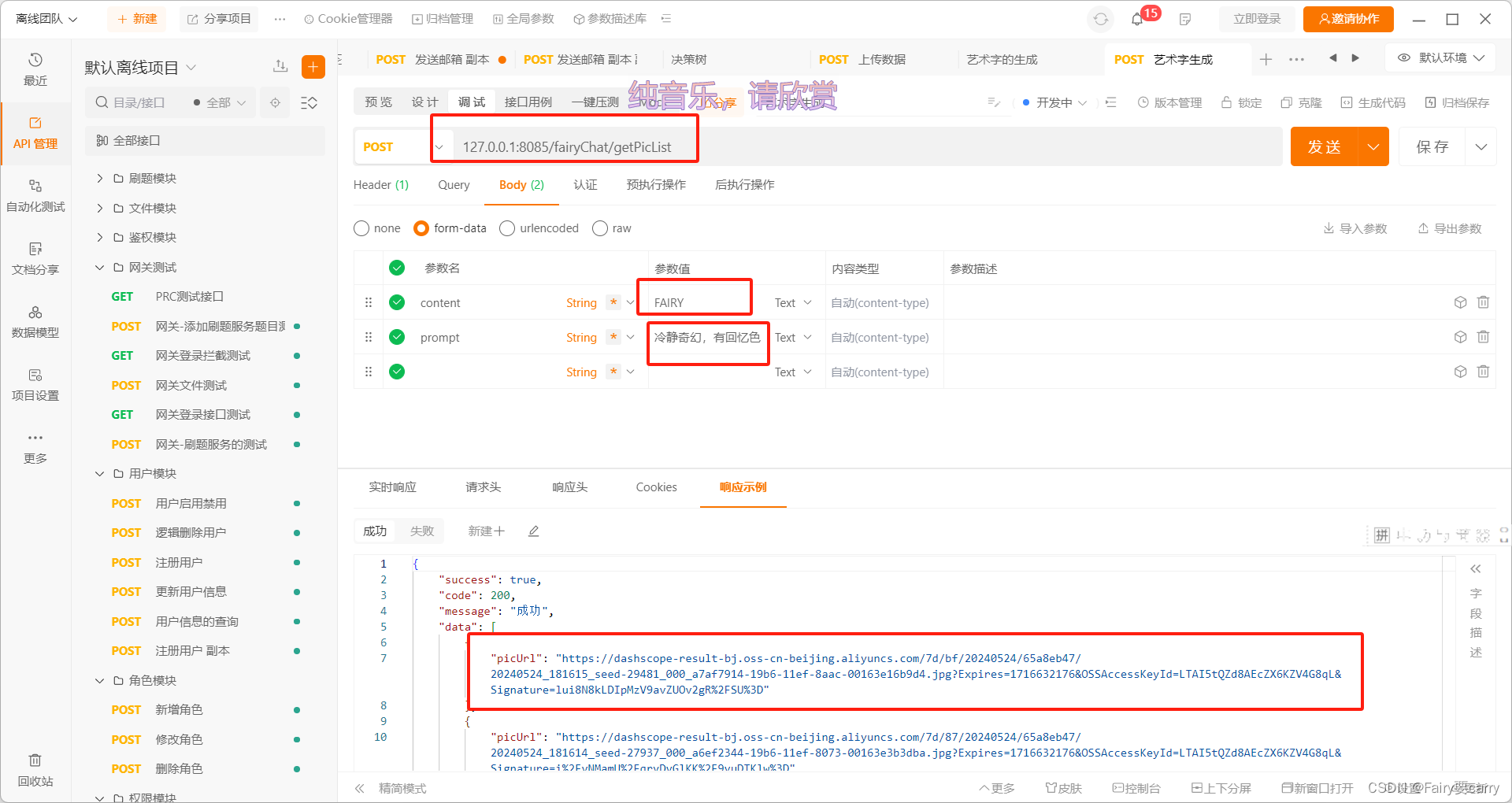
效果图:

后期展望:
1.CNN学习和+复习大模型
2.准备复现一下代码(结合几个大模型CNN,VGG,残差网络ResNet对于图片的分类)或者微调一下大模型(拿到了关于医学的数据)
想学习一下微调大模型。
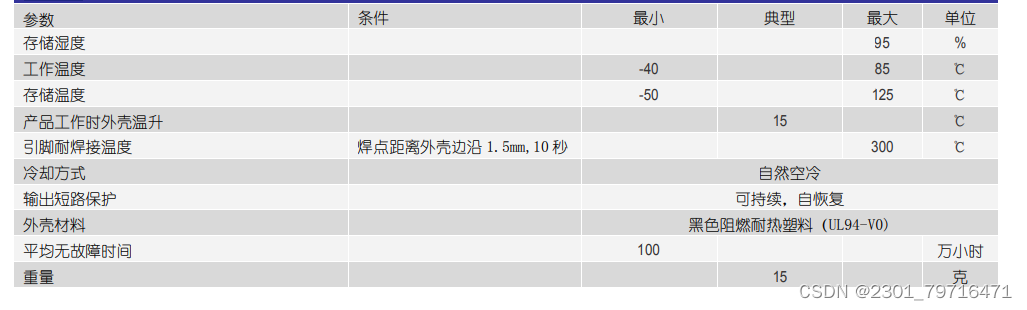
数据如下: