答题结果页 - 蓝桥云课 (lanqiao.cn)
0子2023 - 蓝桥云课 (lanqiao.cn)(暴力枚举

#include<bits/stdc++.h>
using ll=long long;
using ull=unsigned long long;
#define fir first
#define sec second
//#define int llconst int N=1e5+10;
const int mod=1e9+7;int a[N],b[N];void solve()
{
// std::string s;
// std::map<int,std::vector<int>> mp;
// for(int i=1;i<=2023;i++)
// {
// s+=std::to_string(i);
// }
// //std::cout<<s<<'\n';
// for(int i=0;i<s.length();i++)
// {
// if(s[i]=='2'||s[i]=='0'||s[i]=='3')
// {
// mp[s[i]].push_back(i);
// }
// }
// ull ans=0;
// for(auto i:mp['2'])
// {
// for(auto j:mp['0'])
// {
// if(j<i) continue;
// for(auto k:mp['2'])
// {
// if(k<j) continue;
// for(auto p:mp['3'])
// {
// if(p<k) continue;
// ans++;
// }
// }
// }
// }
// std::cout<<ans;std::cout<<"5484660609";
}
signed main()
{//freopen("a","w",stdout);//把结果输出到a.in里面std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}
0双子数 - 蓝桥云课 (lanqiao.cn)(暴力枚举
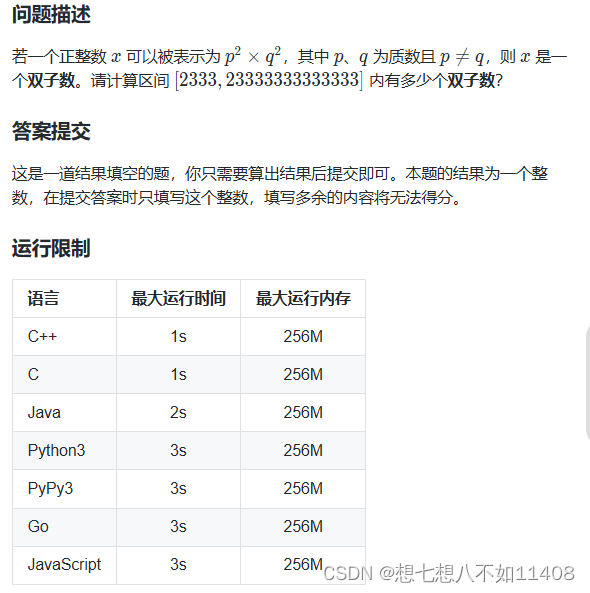
懒得再写一遍【蓝桥杯】国赛普及--CSDN博客
#include<bits/stdc++.h>
using ll=unsigned long long;
#define int ll
const int N=2e5+10;
int k=0;
std::string s;
int a,b,c,d;
bool isprime(int x)
{for(int i=2;i<=x/i;i++){if(x%i==0) return false;}return true;
}
void solve()
{char op;std::cin>>op;if(op=='A'){std::string s;for(int i=1;i<=2023;i++){s+=std::to_string(i); } //std::cout<<s;std::cout<<5484660609<<'\n';ll ans=0;int len=s.length();std::vector<int> v1;std::vector<int> v2;std::vector<int> v3;for(int i=0;i<len;i++){if(s[i]=='2') v1.push_back(i);if(s[i]=='0') v2.push_back(i);if(s[i]=='3') v3.push_back(i);}for(int i=0;i<v1.size();i++){for(int j=0;j<v2.size();j++){if(v2[j]<=v1[i]) continue;for(int k=i+1;k<=v1.size();k++){if(v1[k]<=v2[j]) continue;for(int p=0;p<v3.size();p++){if(v3[p]<=v1[k]) continue;ans++;}}}}std::cout<<ans<<'\n';}else{
// for(int i=1;i<=110000000;i++)
// {
// if(i*i>=23333333333333)
// {
// std::cout<<i;
// break;
// }
// }
//4830549std::vector<int> v;for(int i=2;i<=5000000;i++){if(isprime(i)) v.push_back(i);}//std::cout<<v.size()<<"xxx\n";ll ans=0;for(int i=0;i<v.size();i++){for(int j=i+1;j<v.size();j++){if((double)v[i]*v[i]*v[j]*v[j]<=23333333333333&&v[i]*v[i]*v[j]*v[j]>=2333) ans++;if((double)v[i]*v[i]*v[j]*v[j]>23333333333333) break;}}std::cout<<ans<<'\n';//947293}
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
} 0班级活动 - 蓝桥云课 (lanqiao.cn)(思维题

这题要点思维吧。
我们先数一数可以凑成几对,也就是有几个数的count值大于等于2,记为cnt。然后我们来讨论一下可能的情况:
如果是1 2 2 3这种情况,2凑成了一队剩下的就是1 3,这两个数不是重复的我们随便改一个即可,答案就是(n-cnt*2)/2。
如果是1 2 2 2 2 3,2凑成了一队,剩下1 2 2 3,因为与已经成队的2重复的有2个,因此必须要把这两个改了,然后发现改完可以是1 1 3 3,答案就是2。
因此我们的答案就是在差的队数和重复的必须要改的数中取一个最大值。
#include<bits/stdc++.h>
using ll=long long;
#define int ll
const int N=1e5+10;
int n;
int a[N];
void solve()
{std::cin>>n;std::map<int,int> mp;for(int i=1;i<=n;i++){std::cin>>a[i];mp[a[i]]++;}ll ans=0,cnt=0;for(auto i:mp){if(i.second>=2) {cnt++;//成对的个数 ans+=i.second-2;}}std::cout<<std::max((n-cnt*2)/2,ans);
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cint>>t;while(t--){solve();}return 0;
} 0合并数列 - 蓝桥云课 (lanqiao.cn)(思维题

题意就是给两个数组,这俩数组的和相同,求问最少合并几次能把这俩数组变得一样。
这个题面感觉挺像cf的。
这题突破点就是第一个数字只能和后面的合并,因此一旦第一个数字不同就必须要向后合并。因此我们开两个双端队列进行模拟,每次看队头两个数字是否相同,相同就同时出队,否则把小的那一端出队往后合并。其实就是双指针的思想,双端队列比较好实现。
#include<bits/stdc++.h>
using ll=long long;
using ull=unsigned long long;
#define fir first
#define sec second
#define int llconst int N=1e5+10;
const int mod=1e9+7;int a[N],b[N];
std::deque<ll> l,r;
void solve()
{int n,m;std::cin>>n>>m;for(int i=1;i<=n;i++){std::cin>>a[i];l.push_back(a[i]);}for(int i=1;i<=m;i++){std::cin>>b[i];r.push_back(b[i]);}ll ans=0;while(l.size()){auto x=l.front(),y=r.front();if(x==y) l.pop_front(),r.pop_front();else if(x<y){l.pop_front();auto k=l.front();l.pop_front();l.push_front(k+x);ans++;}else{r.pop_front();auto k=r.front();r.pop_front();r.push_front(k+y);ans++;}}std::cout<<ans<<'\n';
}
signed main()
{//freopen("a","w",stdout);//把结果输出到a.in里面std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}
0数三角 - 蓝桥云课 (lanqiao.cn)(模拟

就是从n个点里选3个,问有几种选法能组成等腰三角形。
被卡常卡了一下午,最后群里大佬帮我改的。
jrz,神!
#include<bits/stdc++.h>
using ll=long long;
using ull=unsigned long long;#define fir first
#define sec second
//#define int llusing PII=std::pair<int,int> ;
const int N=2e3+10;
const int mod=1e9+7;
const double eps=1e-6;double dis(PII& c,PII& d)
{return (c.fir-d.fir)*(c.fir-d.fir)+(c.sec-d.sec)*(c.sec-d.sec);
}
bool line(PII& a,PII& b,PII& c)//共线返回yes
{if(a.sec==b.sec||a.sec==c.sec){return a.sec==b.sec && a.sec==c.sec;//纵坐标相同得全相同才共线}double k1=((a.fir-b.fir)*1.0/(a.sec-b.sec));double k2=((a.fir-c.fir)*1.0/(a.sec-c.sec));return std::abs(k1-k2)<eps;
}
void solve()
{int n;std::cin>>n;std::vector<PII> a;for(int i=0;i<n;i++){int x,y;std::cin>>x>>y;a.emplace_back(x,y);}std::vector< std::map<double,std::vector<int>> > mp(n);ll ans=0;for(int i=0;i<n;i++){auto s=mp[i];for(int j=0;j<n;j++){if(i==j) continue;double d=dis(a[i],a[j]);s[d].push_back(j);//存下与第i个点距离为d的坐标}for(const auto& j:s){auto& ss=j.sec;for(int p=0;p<ss.size();p++){for(int q=p+1;q<ss.size();q++){if(line(a[i],a[ss[p]],a[ss[q]])) continue;ans++;}}}}std::cout<<ans<<'\n';
}
signed main()
{//freopen("a","w",stdout);//把结果输出到a.in里面std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}0删边问题 - 蓝桥云课 (lanqiao.cn)(强连通分量

强连通分量不会,跳了。
0AB路线 - 蓝桥云课 (lanqiao.cn)(BFS

唉,代码写了三个版本。
第一个版本只标记是否走过这点,很显然是不对的,有些点需要重复走,只有30%。
第二个版本四位数组,最后2位分别记录走过几次a和几次,但是会爆数组,只有80%。
第三个版本,因为已知前一个点,那么也就知道它的状态,我们无需知道a和b走过多少次,只需要知道上一个点在当轮走过多少次。 然后就是答案输出距离,好久没写bfs我还卡了一下,直接写个dis数组,初始化为-1标记距离就好。
#include<bits/stdc++.h>
using ll=long long;
using ull=unsigned long long;#define fir first
#define sec second
//#define int llusing PII=std::pair<int,int> ;
using ari=std::array<int,3>;
const int N=1e3+10;
const int mod=1e9+7;
const double eps=1e-6;char g[N][N];
int n,m,k;
int st[N][N][11];
//求出满足条件的最短的路
//必须先k个a再k个b
int dx[]={1,0,-1,0};
int dy[]={0,-1,0,1};ll ans=0;
void bfs(int x,int y)
{std::queue<ari> q;q.push({x,y,1});st[x][y][1]=0;while(q.size()){auto t=q.front();q.pop();if(t[0]==n&&t[1]==m){std::cout<<st[n][m][t[2]]<<'\n';return ;}for(int i=0;i<4;i++){int a=t[0]+dx[i];int b=t[1]+dy[i];if(a<1||b<1||a>n||b>m) continue;if(t[2]==k){if(g[a][b]==g[t[0]][t[1]]) continue;if(st[a][b][1]!=-1) continue;q.push({a,b,1});st[a][b][1]=st[t[0]][t[1]][t[2]]+1;}else{if(g[a][b]!=g[t[0]][t[1]]) continue;if(st[a][b][t[2]+1]!=-1) continue;q.push({a,b,t[2]+1});st[a][b][t[2]+1]=st[t[0]][t[1]][t[2]]+1;}}}std::cout<<-1<<'\n';
}
void solve()
{std::cin>>n>>m>>k;memset(st,-1,sizeof st);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){std::cin>>g[i][j];}}bfs(1,1);
}
signed main()
{//freopen("a","w",stdout);//把结果输出到a.in里面std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}0抓娃娃 - 蓝桥云课 (lanqiao.cn)(二分

首先看到这个题目就感觉透着一股二分左右端点的味,然后就是要注意到一个条件
,没有这个条件的话感觉难很多。
这个条件的意思就是前n个线段的长度全都比任一一个区间的长度要小。
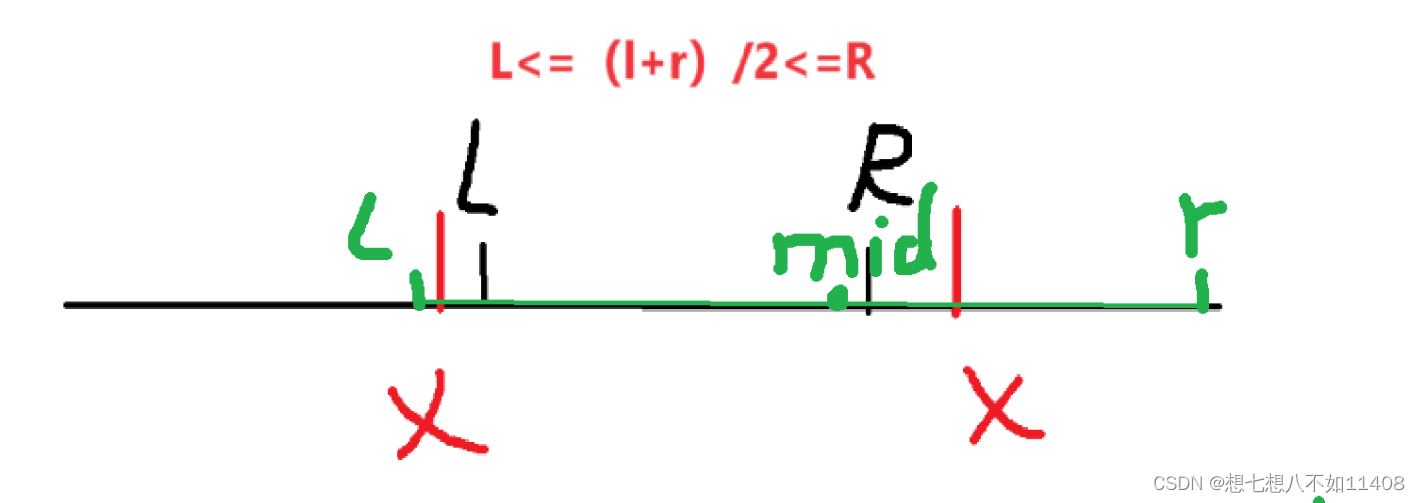
然后我们稍微画个图看看,会发现如果一个线段的中点在区间L的左边或者在R的右边,包不行的。如果在中间呢?由条件这个线段的长度一定是小于当前区间长度,线段被完全包含在这块区间内很显然是可以的,因此我们只讨论线段有一部分在线段外的情况。
如果需要一半区间都在外面,则l必须比L小,此时线段的长度比区间大不满足题目条件。
因此,我们只要找有多少条线段的中点在L,R中即可。
因为double比较麻烦,我们直接同时乘以2。
#include<bits/stdc++.h>
using ll=long long;
using ull=unsigned long long;#define fir first
#define sec second
//#define int llusing PII=std::pair<int,int> ;
using ari=std::array<int,3>;
const int N=1e5+10;
const int mod=1e9+7;
const double eps=1e-6;int n,m;
void solve()
{std::cin>>n>>m;//L<=(l+r)/2<=R//2*L<=(l+r)<=R*2std::vector<int> a(n);for(int i=0;i<n;i++){int l,r;std::cin>>l>>r;a[i]=l+r;}std::sort(a.begin(),a.end());for(int i=0;i<m;i++){int l,r;std::cin>>l>>r;l*=2,r*=2;int L=std::lower_bound(a.begin(),a.end(),l)-a.begin();int R=std::upper_bound(a.begin(),a.end(),r)-a.begin();std::cout<<R-L<<'\n';}
}
signed main()
{//freopen("a","w",stdout);//把结果输出到a.in里面std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}
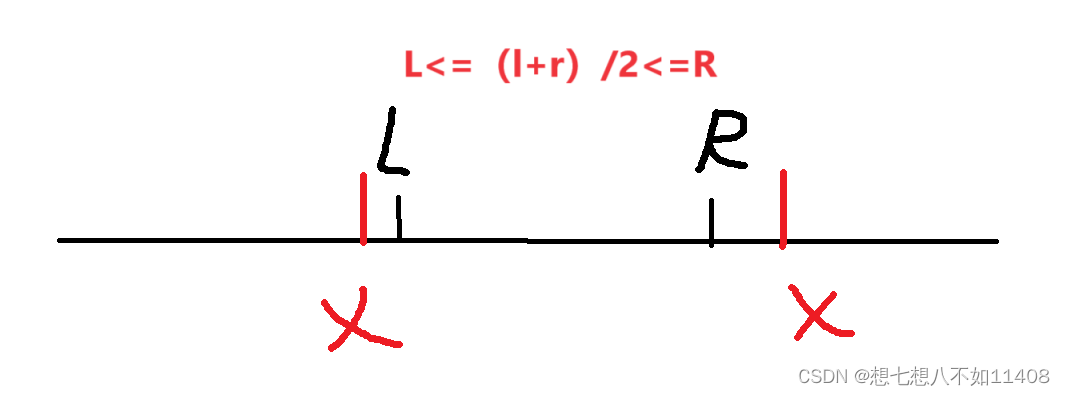



![[FlareOn6]Overlong](https://img-blog.csdnimg.cn/direct/bd9d890dba1e4e76a08a61e25ad399d6.png)