背景
学习极客实践课程《检索技术核心20讲》https://time.geekbang.org/column/article/215243
课程分为基础篇、进阶篇、系统案例篇
主要记录企业课程学习过程课程大纲关键点,以文档形式记录笔记。
内容
检索技术:它是更底层的通用技术,它研究的是如何将我们所需的数据高效地取出来。不管是在数据库和搜索引擎里,还是在新闻推荐平台、电商平台、生活服务平台中,如果我们把这些业务场景抽象出来,它们的本质其实都是在海量的信息中,快速筛选出我们需要的内容或服务,而这都和检索技术紧密相关。
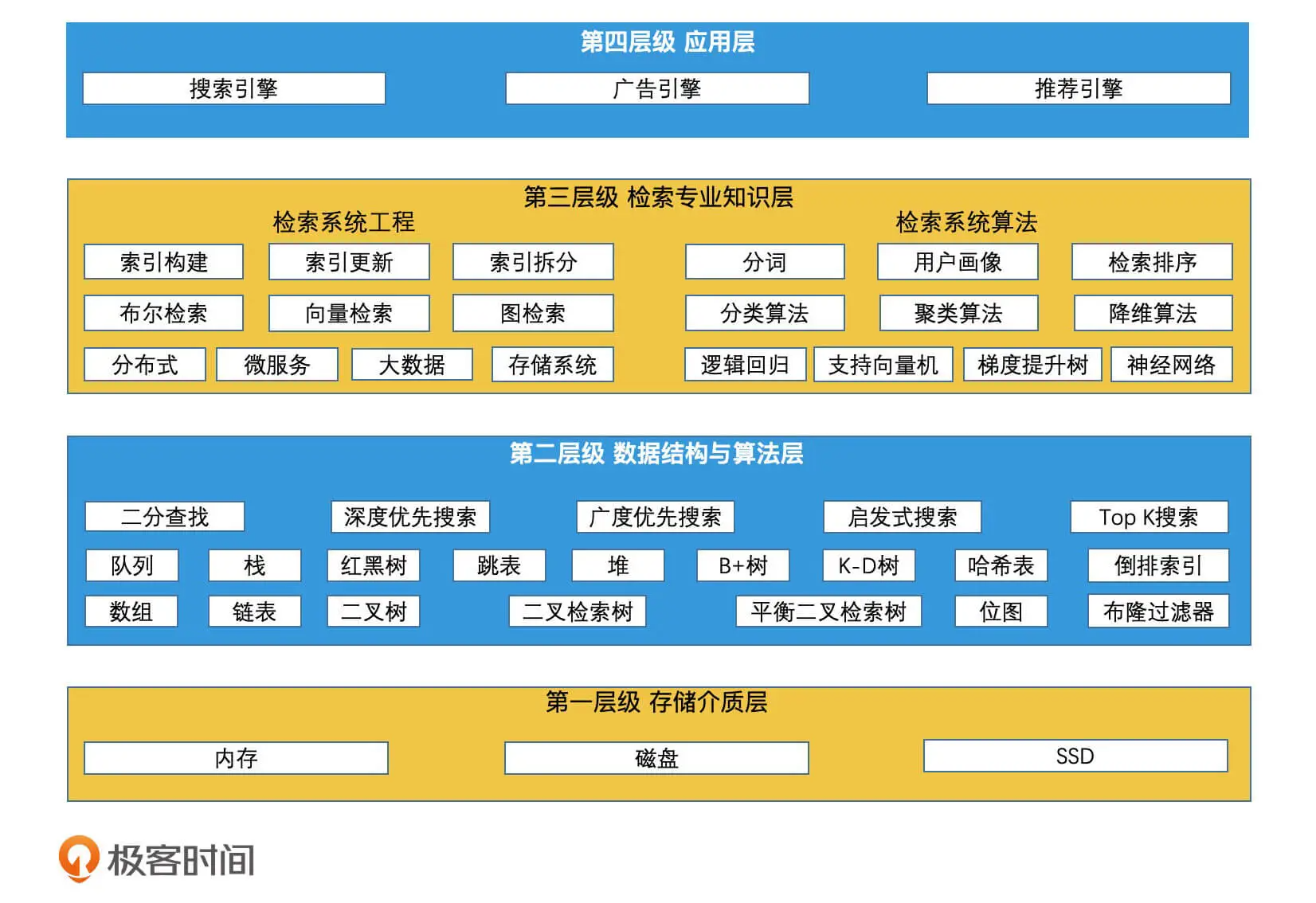
基础篇
顺序结构二分检索
数组的特点:随机访问,存储空间连续剧,增删性能较慢。
链表的特点:顺序访问,存储空间不连续,增删性能较快。
数组和链表分别代表了连续空间和不连续空间的最基础的存储方式,它们是线性表(Linear List)的典型代表。
线性数据结构可以使用二分查找,如数组、链表、队列等,兼顾数组随机访问和链表增删方便的特点,通过灵活改造将链表挂数组中可以一定程度改善 "低效率寻址"的缺点,比如说,我的链表就只有两个节点,每个节点都存储了一个小的有序数组。这样在检索的时候,我可以用二分查找的思想。
一些高级结构都是基于数组、链表组合等方式设计实现的。
思考1:对于有序数组的高效检索,为什莫使用二分查找而不是3-7、4-6分查找?在缺乏分布信息的情况下”,那么二分是效率最优的。如果有了分布信息,比如说,数据是均匀分布的,最小的数是1,最大的数是1000,那么当我们想查询5的时候,我们第一次查询的位置就不是数组中间了,而是在数组前5/1000的位置进行查找。这种基于均匀分布假设的查找方式,叫做“插值查找”。
思考2:单值查询可以使用二分,对于有序区间查询[x,y] 呢?方式1是可以采用两次二分查找分别在所有数据集查询x、y,然后中间元素顺序访问确定区间,方式2是首先一次二分查找x,再从[x,TAIL]进行一次二分查找y,中间元素顺序访问确定区间。方式3首先查找y等。方式1的实践复杂度为log(N) + log(N),方式2的时间复杂度为log(x) + log(y-x)。
树结构二分检索
基础的线性结构可以组合成树结构,树结构实现方式可以是类似链表挂数组(链表节点的数据节点可以是数组,也可以是单值)的结构如BST树,BST树就类似一个书目录,一个磁盘文件夹,主要作用就是快速减少查询范围。
树结构可以巧妙的利用二分查找的特点。前提是这棵树是BST(二叉排序树)
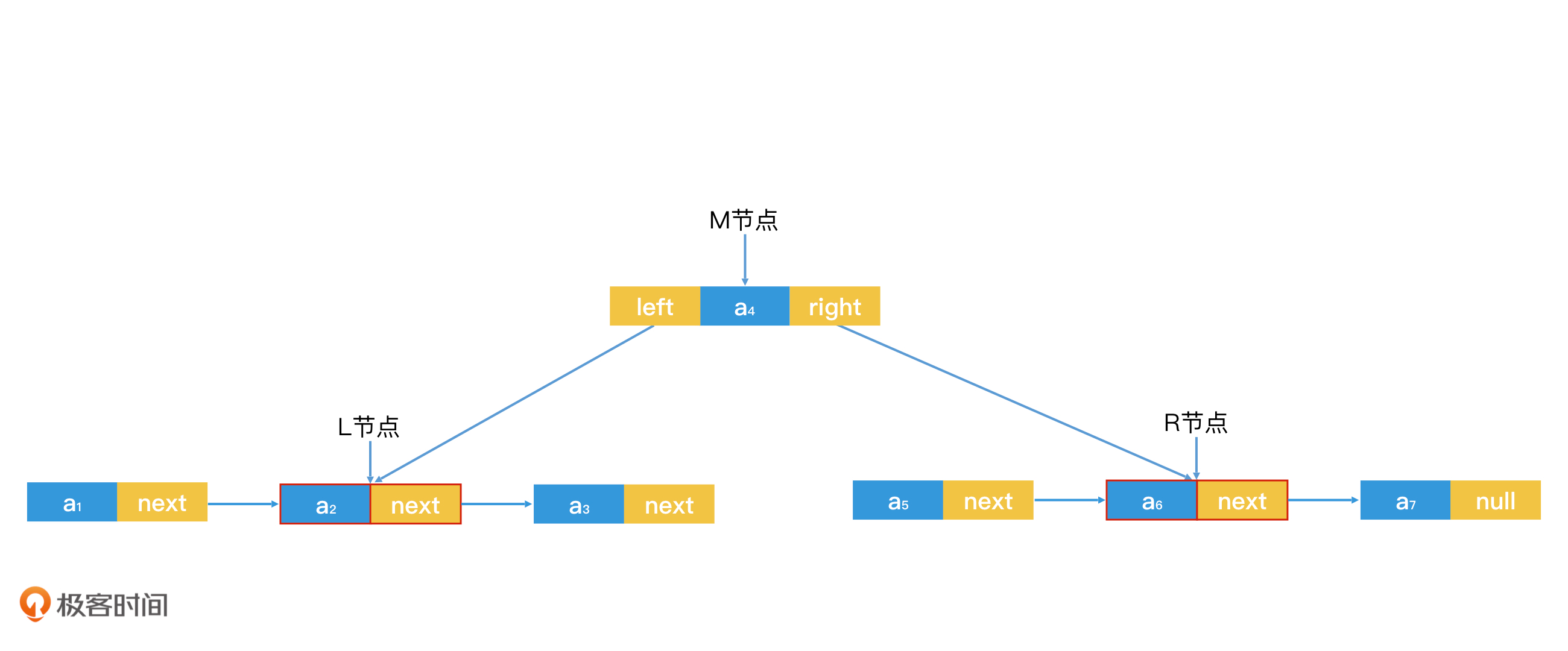
BST面对数据分布不均衡的时候,容易退化为链表,这样就无法达到快速减少 查询范围的目标。
然后出现了AVL、红黑树这样的通过自旋等方式保证BST自平衡的结构。
跳表的二分检索
像Redis中的linkedlist实现方式之一就有使用到跳表。
链表的特点不能随机访问,因此不能很方便的快速到达所需要的位置区间。跳表就是解决这个问题,通过多层的一个链表组织结构,上层的作为下层节点的目录,底层的链表阶段存储数据。上层的节点逐层递增,理想的跳表每层基本数量维持在2的N(0、1、2…)次方。在跳表的论文中,有做实验提到,在random level的实际实现中,将1/2改为1/4,会有一定的检索效率提升。而且空间利用率也会更好。
查找的时候从顶层开始,逐渐在当层右移动、下层移动,最终找到目标区间访问寻找到target。
数据增删的时候,如果要保证理想链表的每隔 2^n 个节点做一次链接的特性,我们就需要重新修改许多节点的后续指针,这会带来很大的开销。因此在检索性能和修改性能做均衡,保证是近似理想状态即可,因此,当新节点插入时,我们不去修改已有的全部指针,而是仅针对新加入的节点为它建立相应的各级别的跳表指针,具体的过程:
- 首先,我们需要确认新加入的节点需要具有几层的指针。我们通过随机函数来生成层数,比如说,我们可以写一个函数 RandomLevel(),以 (1/2)^n 的概率决定是否生成第 n 层。这样,通过简单的随机生成指针层数的方式,我们就可以保证指针的分布,在大概率上是平衡的。
- 在确认了新节点的层数 n 以后,接下来,我们需要将新节点和前后的节点连接起来,也就是为每一层的指针建立前后连接关系。其实每一层的指针链接,你都可以看作是一个独立的单链表的修改,因此我们只需要用单链表插入节点的方式完成指针连接即可。
如插入节点,先找到数据节点单链表也就是最后一层插入节点,此时是最底层单链表的插入,修改上一个节点的pre和插入节点的next指针即可,下面是为生成level节点,具体多少层就是randomLevel()函数决定的,对于每个level,需要从每层的head节点开始,沿着next一直查找需要插入的位置(因为有了数据节点,可以很方便定位current.var < data.val < next.val,主角这样就在current后面插入当前level的指针节点)。
为了保证跳表的检索空间平衡,跳表为每个节点随机生成层级,这样的实现方式比 AVL 树和红黑树更简单。
思考1:什么时候使用红黑树而不是跳表?跳表虽然实现比较简单,理想结构查询效率为log(N),但是跳表性能不太稳定,检索性能最差是O(N),因为跳表是依赖于大量链接的随机分布来提高检索性能的,但是随机分布的性能并不是最优的,在极端情况下还可能退化到O(N)。另外一个点就是内存占用率较高,因为一个节点要带有多个指针,这会带来更大的存储开销。因此,如果我们的应用场景要求检索性能稳定,节省内存,并且没有遍历需求,插入频率也不高的话(红黑树频繁插入数据时,加锁代价会比跳表大),那么使用红黑树更合适。
思考2:跳表能否替代数组? 每个结构都有各自的优缺点,需要针对具体的数据场景合理选择结构,需要不仅仅考虑内存空间效率,数组的确比跳表更加稳定。不过内存碎片化问题,这个会有内存碎片处理来解决。其实,还有两点是很关键的,一个是考虑实际情况,内存有局部性原理,对连续空间的处理会更高效;另一个是考虑范围查找,数组将查询结果成片复制出来效率会更高(内存拷贝技术+内存局部性原理)
哈希检索
在实际应用中,我们经常会面临需要根据键(Key)来查询数据的问题。比如说,给你一个用户 ID,要求你查出该用户的具体信息,如何实现呢?
首先想到的就是将所有key排序,使用数组顺序存储key、val,这样就能实现二分查找。比如用户的 ID 是一个数字,并且范围有限,这样才能申请固定长度的数组空间。
或者使用BST、跳表等实现。这样的平均时间复杂度就是logN。
假如ID是字符串呢?可以采用Hash的方式,将字母映射为数字。一种O(1)的方案就是将key利用Hash函数转为数组下标,利用数组随机访问的特点,
假如ID范围很大,无法申请这莫大空间的数组呢?可以对Hash数值进行特殊计算操作,比如对最大数组长度取余数。这种情况会导致Hash冲突。
线性探测解决哈希冲突:解决Hash冲突的方式有开放寻址法-线性探测,逻辑就是发生冲突之后,就是向前 or 向后 查询可以插入的位置,另外还有指数探测等。查询的逻辑就是找到key对应的数组位置,判断元素是否为空 or 是否和当前key一样,不一样的话就按照约定的如开放寻址法继续寻找,直到找到或者找不到为止。
其他方法解决哈希冲突:哈希冲突会影响哈希表的整体性能,插入和查询的时候都会沿着哈希表进行逐个遍历,复杂度为O(N)。为了解决这个问题,可以采用二次探测、双散列的方式优化。
- 二次探查就是将线性探查的步长从 i 改为 i^2:第一次探查,位置为 Hash(key) + 1^2;第二次探查,位置为 Hash(key) +2^2;第三次探查,位置为 Hash(key) + 3^2,依此类推。
- 双散列就是使用多个 Hash 函数来求下标位置,当第一个 Hash 函数求出来的位置冲突时,启用第二个 Hash 函数,算出第二次探查的位置;如果还冲突,则启用第三个 Hash 函数,算出第三次探查的位置,依此类推。
对于开放寻址法来说,无论使用什么优化方案,随着插入的元素越多、哈希表越满,插入和检索的性能也就下降得越厉害。在极端情况下,当哈希表被写满的时候,为了保证能插入新元素,我们只能重新生成一个更大的哈希表,将旧哈希表中的所有数据重新 Hash 一次写入新的哈希表,也就是 Re-Hash,这样会造成非常大的额外开销。因此,在数据动态变化的场景下,使用开放寻址法并不是最合适的方案。
链表法解决哈希冲突:将冲突的元素使用链表存储起来。

思考1:使用开放寻址法解决哈希冲突的哈希表能直接删除某元素吗?不能直接简单的删除,可以增加一个删除flag。哈希表在查找元素的时候,不是只看下标的,还要对比下标位置的元素值,相同才算找到。这也是为什么会有线性探查等方法。不能直接删除的问题在于,直接删除会把探查序列中断。举个例子:有三个元素a,b,c的hash值是冲突的,那么探查序列会把他们放在三个位置上,比如1,2,3(探查序列是123),如果我们把b删了,那么2这个位置就空了。这时候,要查询c,探查序列就会在2的位置中断,查不到c。
二值状态检索
比如判断一个对象是否存在,查询某个二值状态结果,可以使用数组、跳表等二分查找,也可使用哈希表O(1)查找。是否还有优化方案呢?
使用普通数组的话,我们直接将用户 ID 的值作为数组下标,将该位置的值从 0 设为 1 就可以了。数量很少并且固定比较适合,当数量很大占用空间会比较大,最直观的一个想法就是,使用最少字节的类型来定义数组,比如说,使用 1 个字节的 char 类型数组,或者使用 bool 类型的数组(在许多系统中,一个 bool 类型的元素也是 1 个字节)。它们和 4 个字节的 int 32 数组相比,空间使用效率提升了 4 倍,这已经算是不错的改善了。但是让然很浪费空间,因为表示 0 或者 1,理论上只需要一个 bit。所以,如果我们能以 bit 为单位来构建这个数组,那使用空间就是 int 32 数组的 1/32,从而大幅减少了存储使用的内存空间。
使用哈希表的话,key存储ID,val存储0、1,支持key为字符串,数量很少比较适合,为了解决空间占用大,需要压缩哈希表数组的长度,当数量很大而且不固定范围,可能要面临rehash等,比较占空间和耗时。
针对此种场景,可以使用位图来减少存储空间,但许多系统中并没有以 bit 为单位的数据类型。因此,我们往往需要对其他类型的数组进行一些转换设计,使其能对相应的 bit 位的位置进行访问,从而实现位图。
压缩哈希表长度但是又不能使用线性探测方法解决hash冲突,因为数量足够大,哈希冲突又比较多,这时可以采用线性探测-双散列的思想解决哈希冲突,这就是布隆过滤波器的i思想。
布隆过滤器:就是对一个对象使用多个哈希函数。如果我们使用了 k 个哈希函数,就会得到 k 个哈希值,也就是 k 个下标,我们会把数组中对应下标位置的值都置为 1。布隆过滤器和位图最大的区别就在于,我们不再使用一位来表示一个对象,而是使用 k 位来表示一个对象。这样两个对象的 k 位都相同的概率就会大大降低,从而能够解决哈希冲突的问题了。
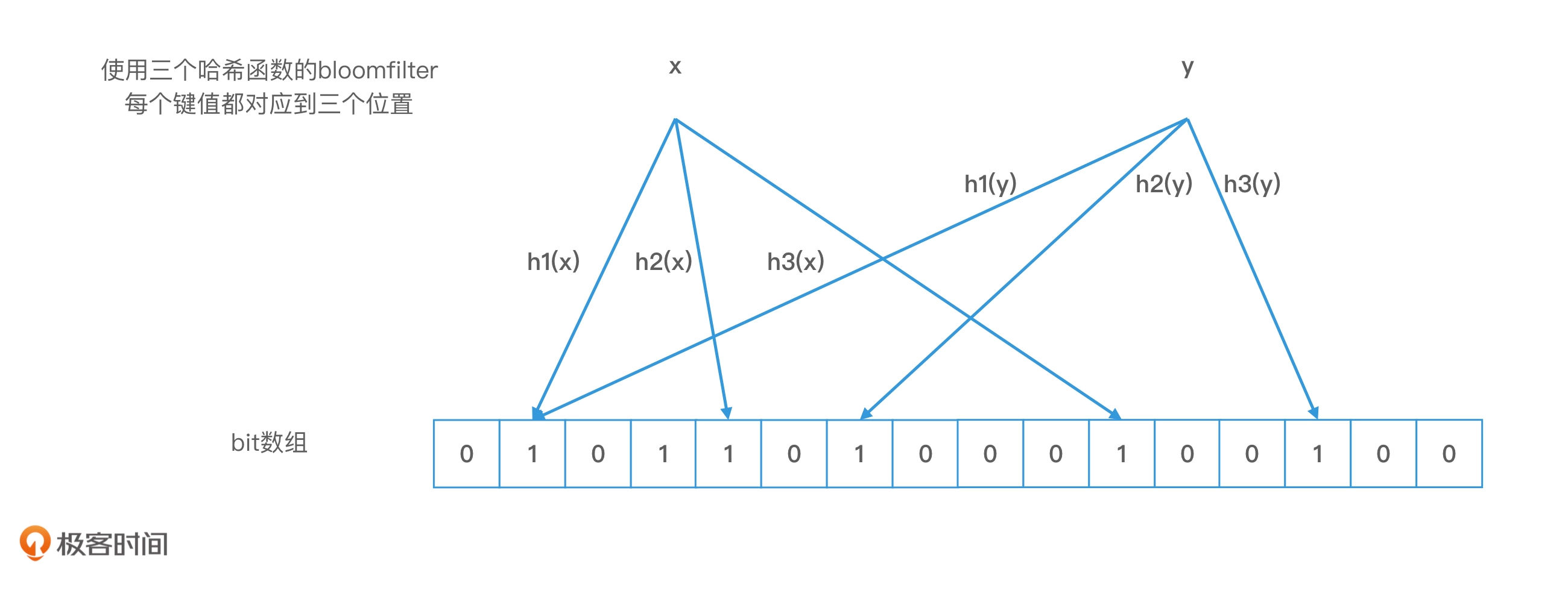
布隆过滤器的错误率:存在一定程度地误判,只能判断一个元素一定不存在,不能判断一个元素一定存在。针对场景我们希望用更小的代价快速判断 ID 是否已经被注册了比较合适。
思考1:布隆过滤器中一个元素能否直接删除?不能直接删除,因为某个位置的状态可能是多个hash函数的即多个元素的映射位置,删了可能会影响其他元素是否存在的判断。有些改进的布隆过滤器采用计数值方式替换0、1,可以解决这个问题,代价就是需要额外额bit来存储计数值。
倒排检索
假如一篇文章包含题目、内容,需要根据关键字查找题目和根据关键字查找内容两个需求,关键字查找题目这个就比较适合正排索引结构如哈希表,第二个根据关键字查找内容使用哈希表就比较费力了,因为需要遍历每个key,获取val在判断有么有包含指定内容,时间复杂度O(K)* O(N),这个时候使用倒排检索结构更合适了。
倒排索引的核心其实并不复杂,它的具体实现其实是哈希表,只是它不是将文档 ID 或者题目作为 key,而是反过来,通过将内容或者属性作为 key 来存储对应的文档列表,使得我们能在 O(1) 的时间代价内完成查询。
创建倒排索引的步骤
- 给文档编号,作为唯一标识,排序,遍历文档。
- 解析出文档关键字,生成<关键字,文档ID,关键字位置>信息。
- 关键字作为key插入哈希表中,如果已经存在就在哈希表的postinglist后面追加节点,记录上面的信息。
- 重复2-3直至处理所有文档。
为什么需要存储关键字位置信息?因为在许多检索场景中,都需要显示关键字前后的内容,比如,在组合查询时,我们要判断多个关键字之间是否足够近。所以我们需要记录位置信息,以方便提取相应关键字的位置。
思考1:如果有个需求是根据文档作者查询文档,怎么设计呢?第一个方案可以对文档的作者设置一个作者标签,为作者标签这些内容创建倒排索引,不再一个内容倒排索引文档中实现,是怕文档内容包含 作者名字 会发生干扰。另一个方案是可以在posting list中加域,标明是作者还是内容,这样就使用一个倒排索引结构就可以了,posting list分域,就是一个元素里加上域标识。举个例子,一篇文章有标题,作者,内容三个域,而“李白”这两个字,可能出现在这三个位置。因此,key和posting list可以这么写: key =“李白” -> [id1,标题域:0,作者域:1,内容域:0],[id2,标题域:1,作者域:0,内容域:1]
思考2:邮件敏感词过滤检测适不适合使用倒排索引?邮件只需要检测一次,因此对邮件做倒排索引并不适用。而且倒排索引也解决不了近义词问题。
邮件敏感词检测一般是这样的思路:
- 准备一个敏感词字典。
- 遍历邮件,提取关键词,去敏感词字典中查找,找到了就说明邮件有敏感词。
这里的核心问题是如何提取关键词和如何在敏感词字典中查询。一种方式是用哈希表存敏感词字典,然后用分词工具从邮件中提取关键字,然后去字典中查。另一种方式是trie树来实现敏感词字典,然后逐字扫描邮件,用当前字符在trie树中查找。
不过,这两种方式都无法解决近义词,或者各种刻意替换字符的场景。要想解决这种问题,要么提供近义词字典,要么得使用大量数据进行训练和学习,用机器学习进行打分,将可疑的高分词找出来。其实这种近义词处理方案,和搜索引擎解决近义词和查询纠错的过程很像。
**为什么需要排序?**查询一个关键字的时候,可以直接获取该关键字下的所有文档信息(文档ID、关键字位置等),如果查询多个关键字,就需要对两条postinglist上的文档信息取交集,如果是无序的,那么时间复杂度为O(M*N),如果是排序的就能使用如归并排序快速排序,时间代价就会将为O(M + N)。
链表归并的过程总结成了 3 个步骤,就是一个双指针的概念
- 第 1 步,使用指针 p1 和 p2 分别指向有序链表 A 和 B 的第一个元素。
- 第 2 步,对比 p1 和 p2 指向的节点是否相同,这时会出现 3 种情况: 两者的 id 相同,说明该节点为公共元素,直接将该节点加入归并结果。然后,p1 和 p2 要同时后移,指向下一个元素; p1 元素的 id 小于 p2 元素的 id,p1 后移,指向 A 链表中下一个元素; p1 元素的 id 大于 p2 元素的 id,p2 后移,指向 B 链表中下一个元素。
- 第 3 步,重复第 2 步,直到 p1 或 p2 移动到链表尾为止。
在倒排索引的检索过程中,两个 posting list 求交集是一个最重要、最耗时的操作,postinglist合并的时候除了使用归并排序,还有跳表、哈希表、位图等结构思想优化效率的方法。
跳表法(相互二分)加速取交集
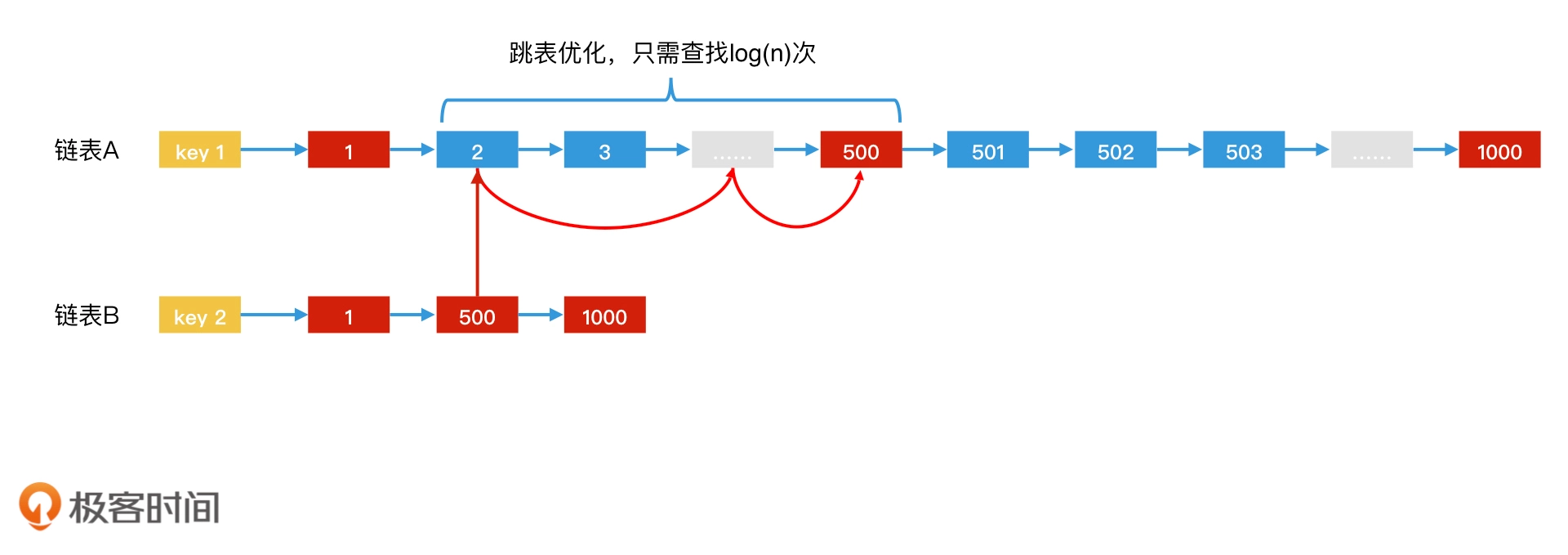
假如归并法遇到下面的情况,那么B的指针需要等待A指针移动(500-2)次才找到交集500。显然数据量大的时候很耗时。
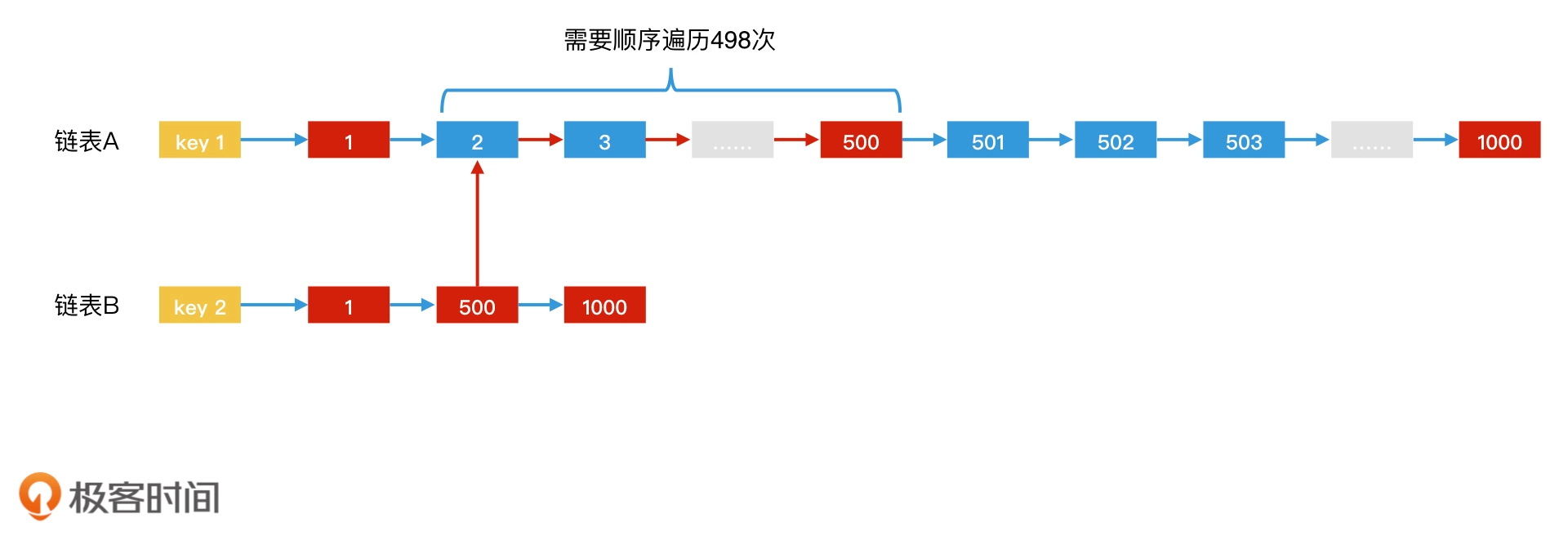 因此可以使用跳表实现postinglist,只需要查找log(500-2)次,后面元素同理,假如A链表比B链表元素稀疏,那就反过来,拿着A的元素去B中二分查找,即互相二分查找。
因此可以使用跳表实现postinglist,只需要查找log(500-2)次,后面元素同理,假如A链表比B链表元素稀疏,那就反过来,拿着A的元素去B中二分查找,即互相二分查找。
在实际的系统中,如果 posting list 可以都存储在内存中,并且变化不太频繁的话,那我们还可以利用可变长数组来代替链表。可变长数组的数组的长度可以随着数据的增加而增加。一种简单的可变长数组实现方案就是当数组被写满时,我们直接重新申请一个 2 倍于原数组的新数组,将原数组数据直接导入新数组中。这样,我们就可以应对数据动态增长的场景。
那对于两个 posting list 求交集,我们同样可以先使用可变长数组,再利用相互二分查找进行归并。而且,由于数组的数据在内存的物理空间中是紧凑的,因此 CPU 还可以利用内存的局部性原理来提高检索效率。
哈希表法加速倒排索引取交集
哈希表加速的思路其实很简单,就是当两个集合要求交集时,如果一个集合特别大,另一个集合相对比较小,那我们就可以用哈希表来存储大集合。这样,我们就可以拿着小集合中的每一个元素去哈希表中对比:如果查找为存在,那查找的元素就是公共元素;否则,就放弃。
查询代价是O(M),如果M的值很大,那么它的性能不一定比跳表法更好了。
但是,使用哈希表法加速倒排索引有一个前提
- 就是我们要在查询发生之前,就把 posting list 转为哈希表。这就需要我们提前分析好,哪些 posting list 经常会被拿来求交集,针对这一批 posting list,我们将它们提前存入哈希表。
- 原始的postinglist也需要保留,哈希表遍历不太方便,后续可能要进行posting list合并。因此倒排字典的key需要指向posting list、哈希表两个结构。
位图法加速倒排索引取交集
位图是特殊的哈希表,使用位图实现posting list可以使用位运算进行检索加速,具体就是为每个倒排字典的key创建长度大小相等的bitmap,如果一个文档信息出现在postinglist中,就将位图中该元素(可以是ID)对应的位置值设置为1。
查询过程如果需要取交集,直接两个bitmap与运算即可,由于位图的长度是固定的,因此两个位图的合并运算时间代价也是固定的。并且由于 CPU 执行位运算的效率非常快,因此,在位图总长度不是特别长的情况下,位图法的检索效率还是非常高的。
局限性
- 仅适合存储ID的简单的postinglist,复杂对象不适合。
- 仅适合元素稠密的场景,如果是稀疏bitmap位运算和存储的开销反而会比使用链表更大。
- 会占用大量空间,每个bitmap必须固定长度,比如ID是int32,那一个bitmap大小就约为512M (2 ^ 16 / 8 / 1024 / 1024 ),如果我们有 1 万个 key,每个 key 都存一个这样的位图,那就需要 5120G 的空间了。
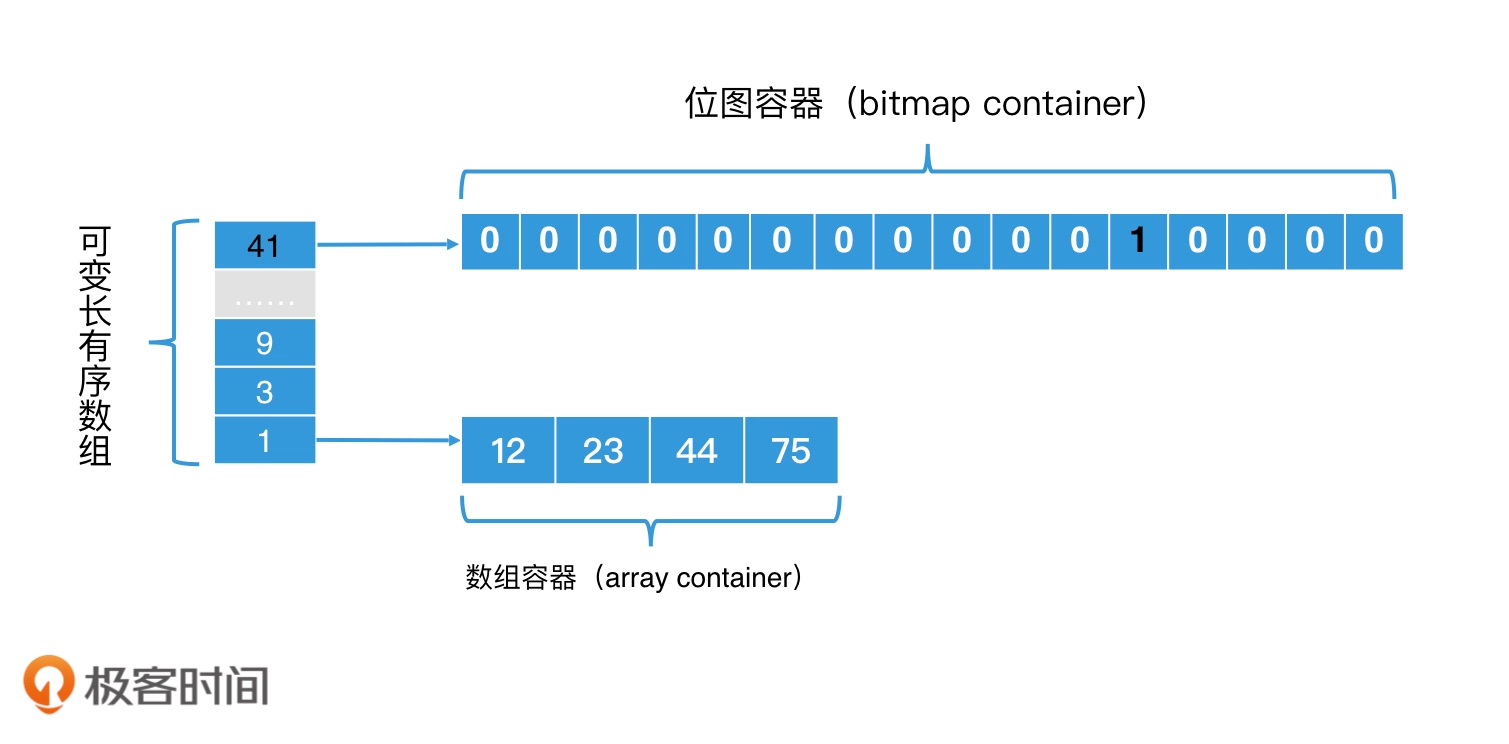
一种升级版位图Roaring Bitmap 可以解决占用空间太多问题Roaring Bimap,设计思想缩短bitmap的bit长度,在前面分层加一个prefix bit 基数数组,比如将一个32bit分为两部分,高16位可表示2^16个桶,低16位表示一个子位图。

这样的话,查询的时候进行两次查询
- 第一步是以高 16 位在有序数组中二分查找,看对应的桶是否存在。如果存在
- 第二步就是将桶中的位图取出,拿着低 16 位在位图中查找,判断相应位置是否为 1。
第一步查找由于是数组二分查找,因此时间代价是 O(log n);第二步是位图查找,因此时间代价是 O(1)。
对于空间占用,假如根据数据分布因为高16位会存在值一样的情况而且一般比较稀疏,这样可以数组,假如所有元素高16位都是相同的
- 在高16位部分,使用一个数组,数组每个元素称为一个桶,桶的空间为 16bit,可以使用可变长数组更节省空间。
- 在低 16 位部分,因为位图长度是固定的,每个都是 2^16 个 bit = 2 ^ 13 byte,那所占空间就是 8K 个字节
相比512M大大节省空间。但是仅限于这种极端情况,假如高16位都不一样,那么高16位有2^16个桶,每个桶对应2 ^ 16 个bitmap。
2 ^ 16 个桶以及对应的2 ^ 16 个低位bitmap空间:2 ^ 16 * 16 bit + 2 ^ 16 * 8 K byte = 2 ^ 19 K byte = 128 K byte + 512M byte = 512M
相比于位图法,这种设计方案就是通过,将不存在的桶的位图空间全部省去这样的方式,来节省存储空间的。而代价就是将高 16 位的查找,从位图的 O(1) 的查找转为有序数组的 log(n) 查找。
每个桶对应子bitmap空间优化:当位图元素太稀疏的时候,还不如直接使用数组,因为一个位图也要占用16bit,当元素格式少于4096时候,使用初始默认4长度的数组,随着数量增对大于4094,就动态的使用位图容器。
RoaringBitmap取交集的过程
- 第 1 步,比较高 16 位的所有桶,也就是对这两个有序数组求交集,所有相同的桶会被留下来。
- 第 2 步,对相同的桶里面的元素求交集。这个时候会出现 3 种情况,分别是位图和位图求交集、数组和数组求交集、位图和数组求交集。其中,位图和位图求交集,我们可以直接使用位运算;数组和数组求交集,我们可以使用相互二分查找(类似跳表法);位图和数组求交集,我们可以通过遍历数组,在位图中查找数组中的每个元素是否存在(类似哈希表法)。
思考1:在 Roaring Bitmap 的求交集过程中,有位图和位图求交集、数组和数组求交集、位图和数组求交集这 3 种场景。那它们求交集以后的结果,我们是应该用位图来存储,还是用数组来存储呢?考虑到交集元素的数量数组和数组求交集、位图和数组求交集 这两种情况可以很容易的想到是使用数组.
但是位图和位图的交集,需要根据情况而定,可以使用预判方法,假设A有a个值,B有b个值,按照平均可以算下间隔,比如位图支持总个数为216,那么A的平均值间隔为216 / a,B的平均值间隔2^16 / b,二者相乘为交集的间隔,那么交集的个数大致为 a * b / (2 ^16 ),最后在和4096比较即可。
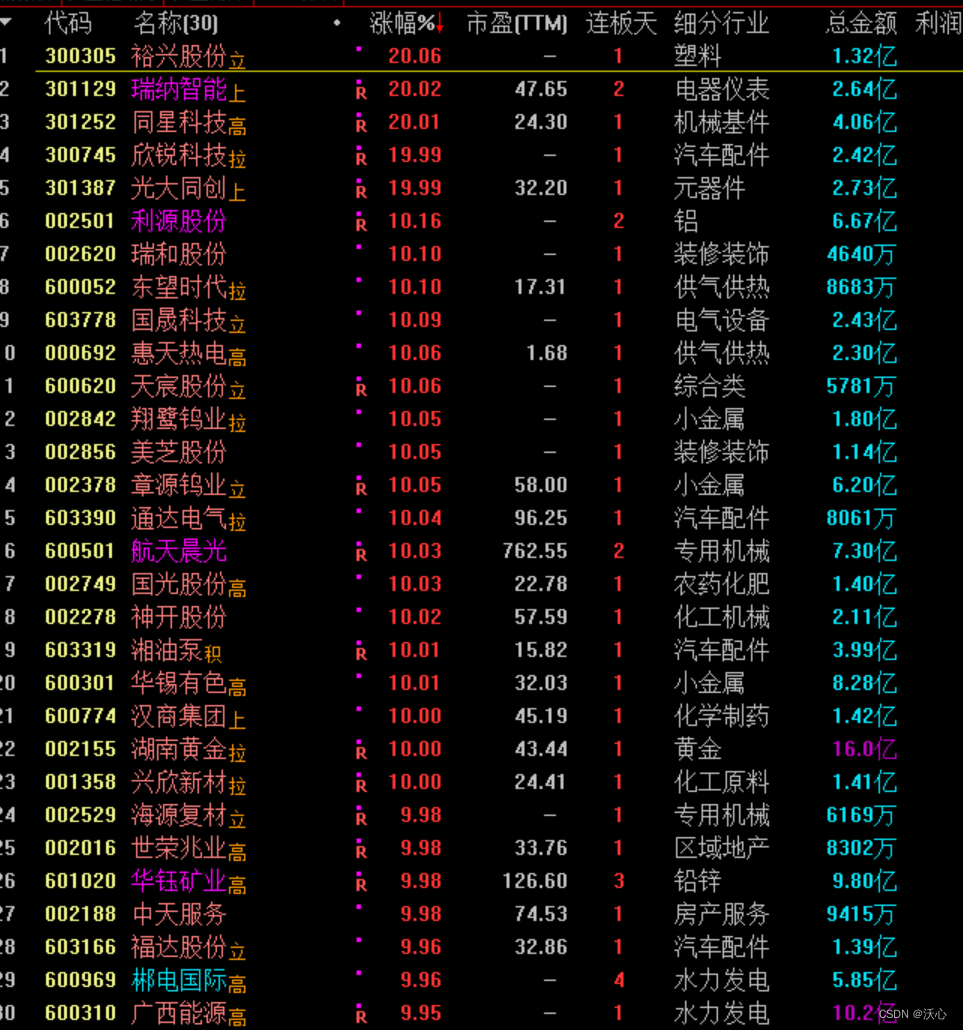
百万并发场景中倒排索引与位图计算的实践_倒排索引_京东科技开发者_InfoQ写作社区
联合查询中加速取交集方法
假如在一个系统的倒排索引中,有4个不同的key对应四类标签的用户,现在需要进行组合key联合查询。
比如在“北京”或在“上海”,并且使用“安卓”的用户集合。抽象成联合查询表达式就是,(“北京”∪“上海”)∩“安卓”;
对于联合查询,在工业界中有许多加速检索的研究和方法,比如,调整次序法、快速多路归并法、预先组合法和缓存法。
调整次序法
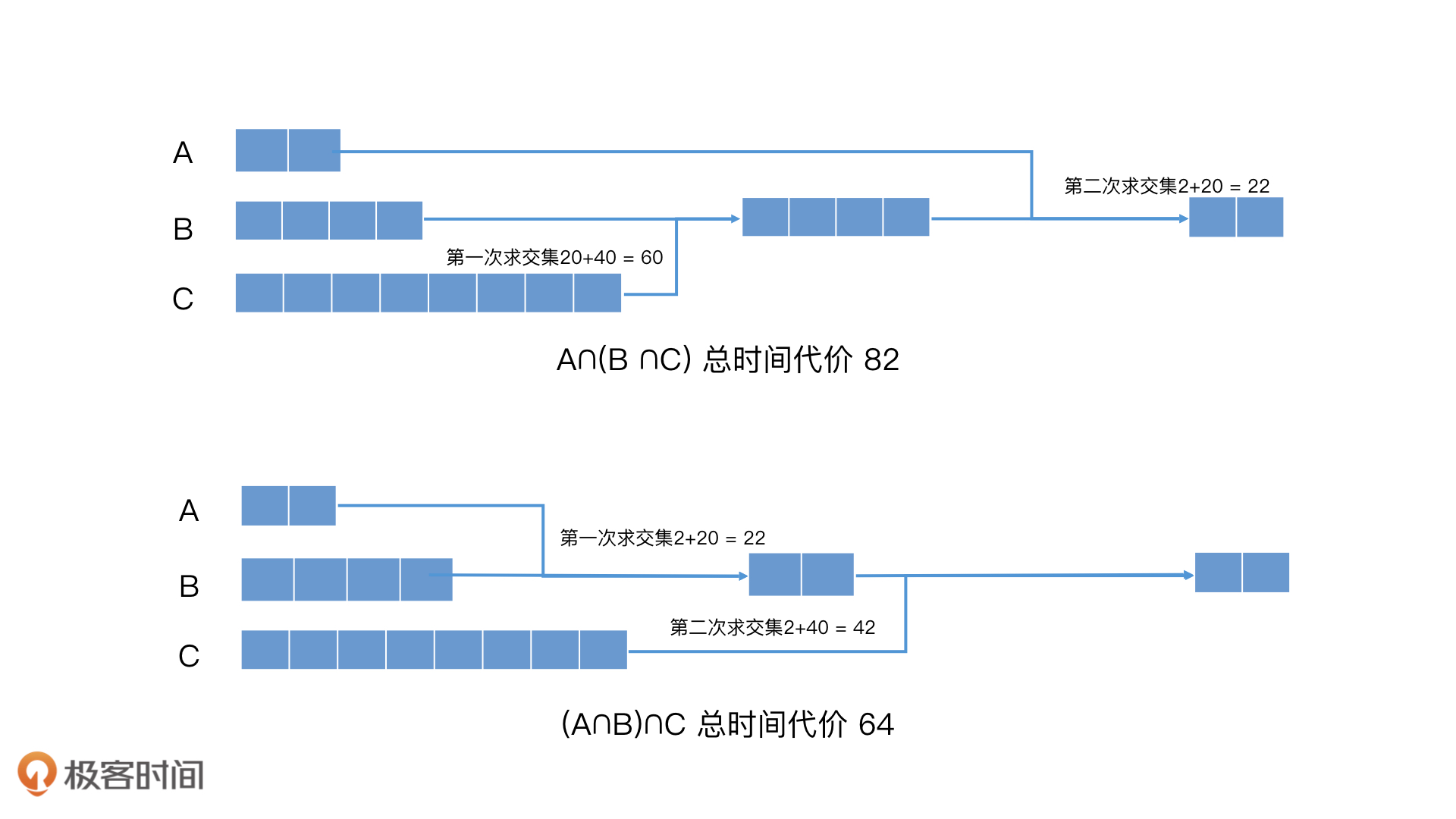
- 连续集合(有包含关系)求交集,通过分析key对应集合的数量,先排序,按照从小到大的集合互取交集,这样时间复杂度更低。
- 连续并集合然会与另外集合取交集,对于并集合中子集合和需要取交集的集合元素数量、值相差比较大的时候,可以根据分配率,逐个与另外集合取交集,最后在合并。
总是就是利用集合的各种公式定律如交交换率(A∩B)∩C = A∩(B∩C)、分配率A∩(B∪C)=(A∩B)∪(A∩C)等根据集合元素特性选择合适的计算顺序。
但是,调整次序法有一个前提,就是集合的大小要有一定的差异,这样的调整效果才会更明显。
快速多路归并法
在对多个 posting list 求交集的过程中,我们可以利用跳表的性质,快速跳过多个元素,加快多路归并的效率。这种方法,我叫它"快速多路归并法"。
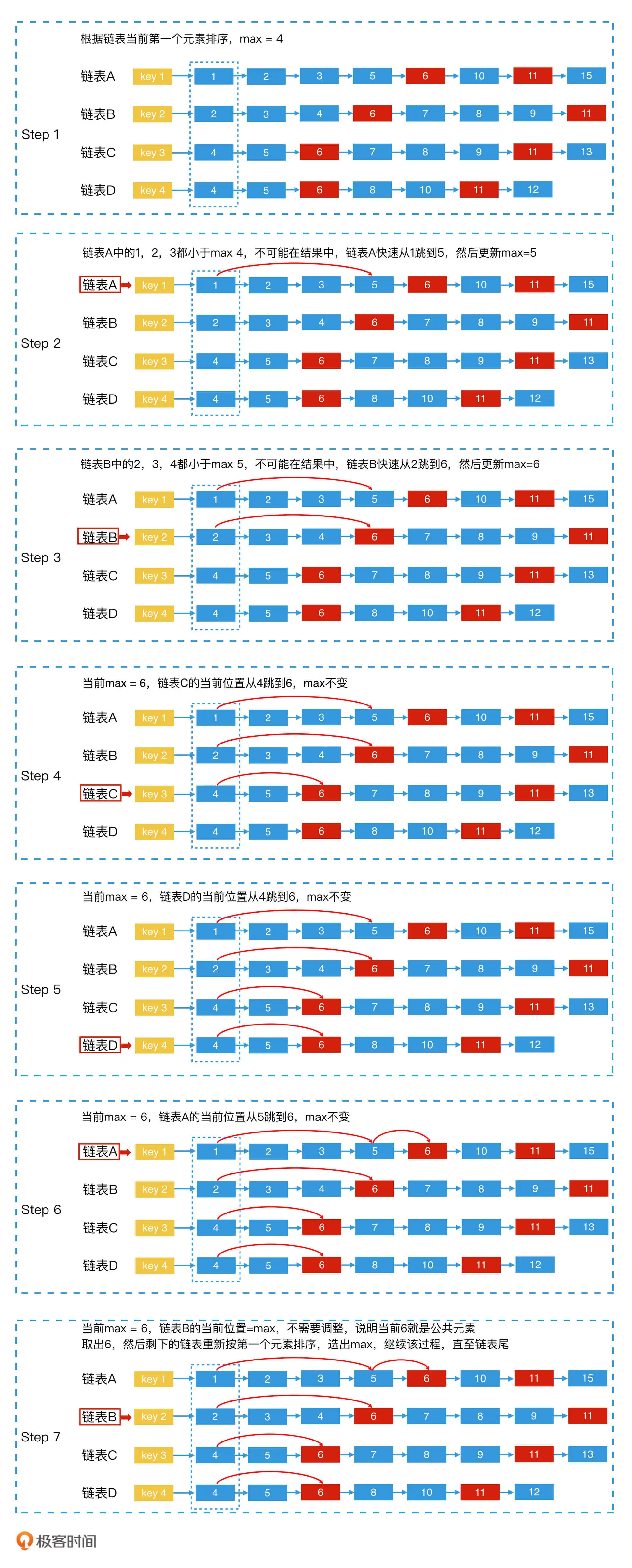
快速多路归并法的思路和实现都非常简单,就是将 n 个链表的当前元素看作一个有序循环数组list[n]。并且,对有序循环数组从小到大依次处理,当有序循环数组中的最小值等于最大值,也就是所有元素都相等时,就说明我们找到了公共元素。
如四个链表A、B、C、D求交集
- 第一步,四个指针指向4个链表的第一个元素,更新最大值max
- 第二步,各个链表当前指针值和max对比
- 如果都像等,max为公共元素,记录此值,每个链表后移指针。
- 如果某个链表当前值 < max,利用跳表法快速调整指针到 >= max 的位置,如果如果新位置元素的值大于 max,则更新 max 的值。继续其他链表。
处理完第四个链表后循环回到第一个链表,用循环数组实现,直到链表全部遍历完。
快速多路归并法适用在要归并的key较多且posting list较长的情况下。否则频繁的排序调整也是一个额外开销。
预先组合法
就是将常出现的查询结果缓存起来,假设,key1、key2 和 key3 分别的查询结果是 A、B、C 三个集合。如果我们经常会计算 A∩B∩C,那我们就可以将 key1+key2+key3 这个查询定义为一个新的组合 key,然后对应的 posting list 就是提前计算好的结果。之后,当我们要计算 A∩B∩C 时,直接去查询这个组合 key,取出对应的 posting list 就可以了。
缓存法加速
预先组合法适合一些常出现的查询,对于某些搜索引擎以及一些具有热搜功能的平台中,经常会出现一些最新的查询组合。这些查询组合请求量也很大,但是由于之前没有出现过,因此我们无法使用预先组合的方案来优化。这个时候,我们会使用缓存技术来优化。
比如使用LRU缓存实现将某次联合查询的结果保存起来,一般是双链表加哈希表实现LRU机制方案。
- 双链表:一个合适的实现方案是使用双向链表:当一个元素被访问时,将它提到链表头。
- 哈希表:优化链表元素访问速度,O(1)获取元素,将元素作为key,元素所在链表节点的地址作为value
思考1:为什么最好使用双链表而不是单链表?因为查询节点k之后,需要节点k移动到链表的头部,假如查询的时候位置在整个LRU的中间,如果链表是单链表的话,那么如何把k节点从链表中摘取出来,然后链表还不能被打断,这就成了一个问题了。因此,我们用双向链表,就可以快速地找到k节点的前序节点,这样就能完成节点k的摘取操作。