数组专题之子数组+二维数组
- 子数组
- 238.除自身以外数组的乘积
- 560.和为K的子数组
- 二维数组
- 48.旋转图像
子数组
数组的子数组问题是算法中常见的一类问题,通常涉及到数组的连续元素。在解决这类问题时,常用的方法有前缀和、滑动窗口、双指针,分治法、动态规划等。下面分别对这几种方法进行简要说明:
- 滑动窗口(Sliding Window):
- 适用于求解和为特定值、最大子数组和、最小子数组和、连续子数组的最大/最小值等问题。
- 通过维护一个固定大小的窗口,在遍历数组的过程中不断移动窗口的位置,从而解决问题。
- 常用于优化时间复杂度,避免重复计算。
- 双指针(Two Pointers):
- 适用于求解有序数组中的问题,如两数之和、三数之和、有序数组中的区间和等。
- 通常使用两个指针,一个从左向右移动,一个从右向左移动,或者一个指针固定,另一个指针移动。
- 通过指针的移动,可以高效地找到满足条件的元素或子数组。
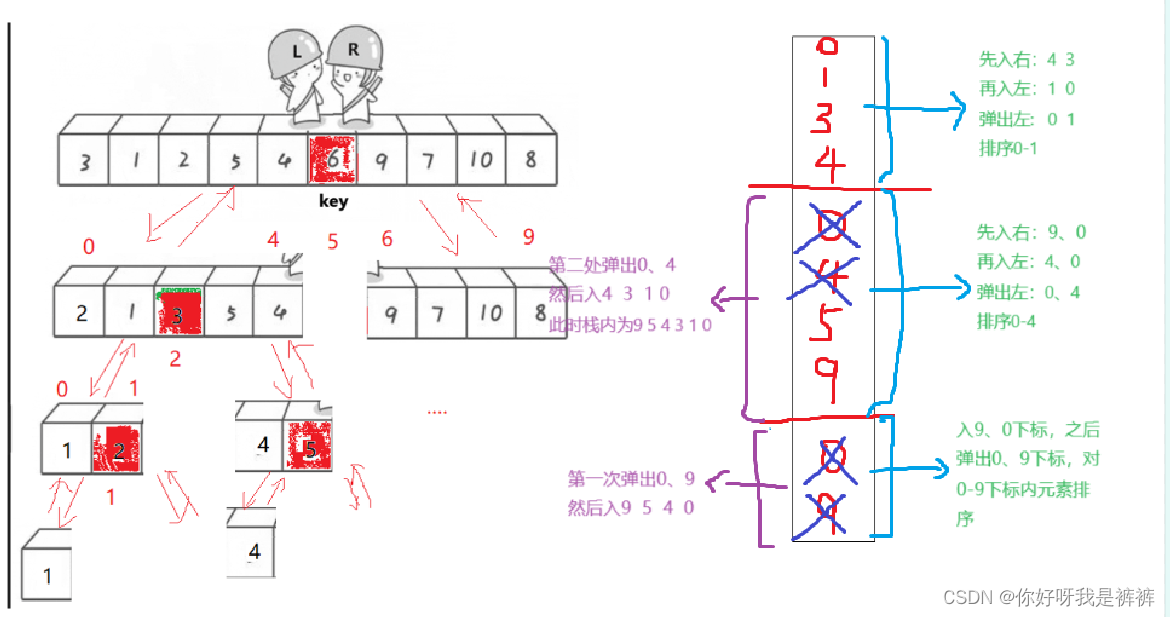
- 分治法(Divide and Conquer):
- 适用于求解数组排序、数组划分等问题。
- 将问题分解为若干个规模较小的相同问题,递归解决,最后合并结果。
- 可以有效利用递归和分而治之的思想,解决复杂问题。
- 动态规划(Dynamic Programming):
- 适用于求解最优解问题,如最长递增子序列、最长公共子序列、最长连续子数组等。
- 通过将问题分解为更小的子问题,并存储子问题的解,避免重复计算。
- 常用于优化时间复杂度,减少冗余计算。
- 前缀和(Dynamic Programming):
- 计算数组的前缀和并存储。
- 遍历前缀和数组,记录下所有满足条件的子数组。
在实际编程中,选择哪种方法取决于问题的具体性质和需求。滑动窗口和双指针通常用于优化时间复杂度,而分治法和动态规划则适用于更复杂的问题。在解决数组子数组问题时,可以根据问题的特点和需求,灵活运用这些方法。
238.除自身以外数组的乘积
思路:
本题需要得到数组中每个元素除本元素之外的所有元素的乘积的子数组,可以先计算出nums[i]左边元素的乘积,并计算出nums[i]右边元素的乘积,最后将两部分结果乘起来就是最后的结果,最后所有的结果保存到ans数组中,以下是一个栗子。

时间复杂度:
时间复杂度是 O(n),其中 n 是数组 nums 的长度。
代码实现:
class Solution {public int[] productExceptSelf(int[] nums) {int[] ans = new int[nums.length];ans[0] = 1;//将nums[i]左边的元素的乘积存在ans[i]里for(int i = 1;i < nums.length;i++){ans[i] = ans[i - 1] * nums[i - 1];}int rigth = 1;//将nums[i]右边的元素累乘到rigth中for(int i= nums.length - 1;i >= 0;i--){ans[i] *= rigth;rigth *= nums[i];}return ans;}
}
560.和为K的子数组
思路:
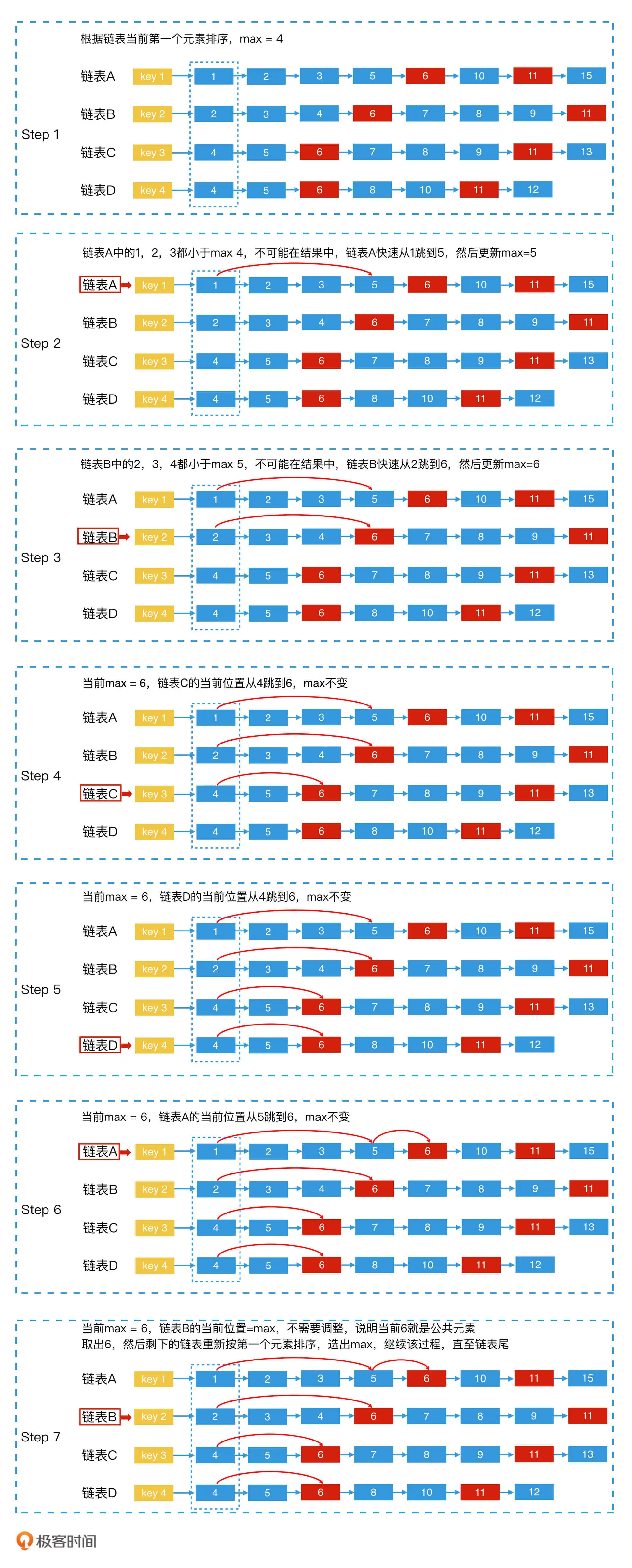
使用一个哈希表记录数组所有的前缀和和出现的次数,以前缀和为key,出现的次数为value,判断在哈希表中是否存在sum - k这个键值,若存在说明出现和为K的连续子数组,下面是一个图示:

在哈希表中存储到每一个元素的前缀和,,那么到j的前缀和和到i的前缀和相减,如果等于K,则说明该子数组和为K,所以可以得到 sum(0,j) - K = sum(0,i - 1),如果哈希表中有sum(0,j) - K这个键值,说明存在和为K的子数组,此时需要将对应的value值与ans相加。
时间复杂度:
时间复杂度为O(n),其中n是数组nums的长度。
代码实现:
class Solution {public int subarraySum(int[] nums, int k) {Map<Integer,Integer> record = new HashMap<>();int sum = 0;int ans = 0;//一定要初始化,初始化record是为了解决累加和等于k的情况。//如果不进行初始化操作,可能会导致错误的计算结果record.put(0,1);for(int i = 0;i < nums.length ; i++){sum += nums[i];if(record.containsKey(sum - k)){ans += record.get(sum - k);}record.put(sum, record.getOrDefault(sum, 0) + 1);}return ans;}
}
二维数组
对于二维数组的旋转问题,找到对应的规律就可以很快的解决。
48.旋转图像
思路:
对二维数组进行顺时针90°的旋转,可以拆分成先将数组按照主对角线进行翻转,然后再将得到的数组左右翻转,模拟的过程如图所示,所以只需要对数组进行两次循环先进行主对角线翻转,然后进行左右翻转即可,详细的讲解点击视频讲解-旋转图像。

时间复杂度:
用到了两层for循环,故时间复杂度为O(n^2)。
代码实现:
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;//按主对角线翻转for(int i = 0; i < n; i++){for(int j = 0; j < i; j++){int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}//左右翻转for(int i = 0; i < n; i++){for(int j = 0; j < n / 2; j++){int temp = matrix[i][j];matrix[i][j] = matrix[i][n - j - 1];matrix[i][n - j - 1] = temp;}}}
}