【机器学习】支持向量机（SVM）

一、概述

支持向量机（Support Vector Machine，简称SVM）是一种对数据进行二分类的广义线性分类器，是一种监督学习算法，其决策边界是对学习样本求解的最大边距超平面。

SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险，是一个具有稀疏性和稳健性的分类器。

SVM可以通过核方法进行非线性分类，是常见的核学习方法之一。

总结来说，SVM有三大核心，分别是最大边距超平面、对偶问题以及核方法

二、最大边距超平面

在讲解最大超平面之前，先讲一下什么是线性可分。

线性可分是分类问题中的一个基础概念，它指的是在特征空间中，存在一个超平面（在二维空间中为一条直线，三维空间中为一个平面，更高维度则为超平面），使得所有属于一个类别的样本点都位于该超平面的同一侧，而所有属于另一个类别的样本点都位于该超平面的另一侧。换句话说，存在一个线性函数（或超平面）可以将不同类别的样本完全分开。

考虑一个二维数据集，其中红色“×”表示第一类样本，蓝色“√”表示第二类样本。如果能在二维平面上找到一条直线将这两类样本完全分开，则称该数据集是线性可分的。

然而，对于线性可分的数据集，可能存在多个超平面都能将数据分开。为了找到最佳的超平面，我们引入了支持向量机（SVM）算法。SVM算法认为最佳的超平面应该满足以下条件：

1.完全可分性：能够将训练集中的不同类别样本完全分开。
2.稳健性：对训练集中的噪声和异常值具有较好的鲁棒性。
3.最大间隔：与样本数据之间的间隔达到最大。

这里的“间隔”是指两侧样本点到超平面的最短距离之和，通常简称为“边距”（Margin）。为了找到最大间隔的超平面，我们需要考虑距离超平面最近的那些样本点，即支持向量（Support Vectors）。这些支持向量决定了最大间隔超平面的位置。

在SVM中，我们试图最大化边距，即找到距离超平面最近的样本点到超平面的距离之和 margin = min(d1 + d2)，并确保这个距离之和在所有可能的超平面中是最大的。这样的超平面就被称为最大边距超平面（Maximum Margin Hyperplane），也是我们在SVM算法中寻求的最佳超平面。通过求解一个优化问题，SVM可以找到这个最大边距超平面，并使用它来对新数据进行分类。

转化为数学公式为：

$Max\left ( margin \right ) = Max\left ( min\left ( d1+d2 \right ) \right )$

点到直线的距离d：点W（Xw,Yw）到直线AX+BY+C=0的距离等于：

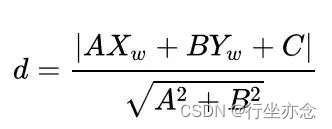
假设样本集中存在一个超平面 $W^{T}x+b = 0$ ，使得样本集线性可分，那么样本到样本超平面的距离d为：

图中可知，无论k 值取多少，都是在 $W^{T}x+b = 0$ 移动k个单位，对超平面的W并不影响

这里令 $W^{T}x+b = 1$ 可得：

但是最大边距超平面转换为数学优化问题还有一个前提，也就是这个超平面能否把样本正确地分类:

对于每个样本点 $\left ( x_{i},y_{i} \right )$ ，其约束条件可以表示为 $y_{i}(w\cdot x_{i}+b)\geq 1$ 。

最大化W范数分之一等价于等价于最小化1/2W范数的平方（凸优化）：

最终优化结果可得：

三、对偶问题：

支持向量机（SVM）原问题是一个二次规划问题，其目标是最大化间隔，同时满足一些不等式约束条件。通过对原问题进行拉格朗日乘数法，我们可以得到对偶问题，即在满足约束条件的前提下最大化拉格朗日函数的值。这种变换使得问题更加易于求解，因为对偶问题往往具有更好的数学性质，如凸性和可分离性等。

从算法角度来看对偶问题引入可以有更多的好处：

将原问题中的非线性分类问题转化为线性分类问题，从而可以通过线性分类的方法来解决。
引入核函数，能够不用知晓具体的维度转换函数直接获得数据的高维度差异度
对偶问题的解往往具有稀疏性，即只有少数几个支持向量对决策边界有贡献。这使得模型更加简洁、易于解释，并且减少了计算成本。

不带约束条件：

对于不带约束条件的优化问题，直接对目标函数求到取极值就可以了。

带等式约束条件：

对于存在等式约束条件，我们先使用拉格朗日乘数法将约束条件融入目标函数，有条件约束问题转化为无条件约束问题·进而求解。

带不等式约束条件：

对于带不等式约束条件，我们先寻找其满足KKT条件的点，以达到满足约束、线性相关，以及在最优解处的特性（等式约束与拉格朗日乘子的乘积为零）。因为KKT点通常为潜在最优解。

将上面原问题的最终优化结果转化为对偶问题（硬间隔）为：

四、软间隔：

在实际应用当中，由于某些数据分布的影响，我们很难找到一个可以将其线性可分的超平面，也就是很难将其正确地分类，所以，SVM引入了软间隔这一概念。软间隔允许在一定的范围内出现错误的样本点，即允许部分样本点不满足硬间隔的要求。具体来说，软间隔通过在目标函数中引入一个损失函数（如hinge损失）来实现，该函数可以度量分类错误的程度大小。在优化过程中，软间隔支持向量机会尽量最大化间隔，同时使分类错误的样本点尽可能少。这样，就可以在一定程度上平衡分类器的泛化能力和对噪声的鲁棒性。

在被错误的数据影响之后，我们仍然能通过支持向量机找到一个次优解，，不过需要允许有错误的点处于这个间隔之内，也就是说对于任何一个样本点不再是大于等于一而是放宽了距离限制

$y_{i}(w\cdot x_{i}+b)\geq 1-\xi _{i}$

$\xi _{i}$ 就是一个松弛变量。

在优化问题中我们也增加了一个惩罚项，其中 $\xi _{i}$ 是一个大于等于零的数。

软间隔的优化问题根据拉格朗日乘数法构建其对偶问题的最终结果：

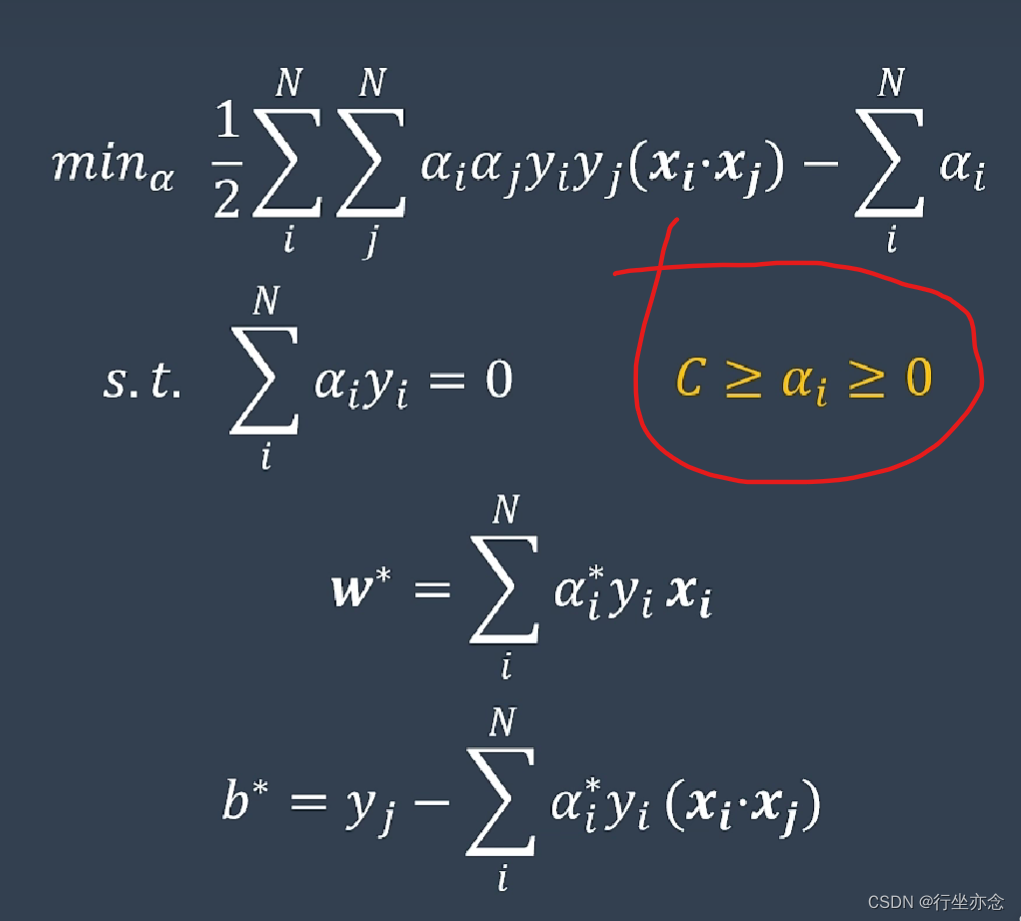
可以看到其结果跟硬间隔对偶问题的结果大致上是一样的，只是约束条件不相同。

五、核函数

核函数可以将输入数据从原始空间映射到一个更高维的特征空间，使得原始数据在新的特征空间中呈现线性可分的特性。这样，原本在原始空间中非线性可分的问题，在映射后的高维空间中就变得线性可分了，从而扩展了SVM的应用范围。

核函数的作用主要是解决线性不可分问题，并且避免了“维数灾难”，减少了计算量。它的一般形式为K(x,y)，其中x和y是输入数据，K(x,y)表示x和y在特征空间上的内积。

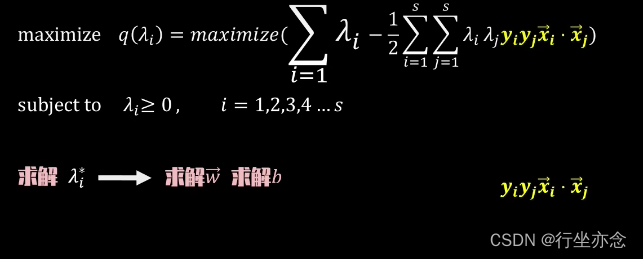
在遇到非线性分类SVM问题时，以上目标方程在原维度下无解，这就要进行升维转换，也就是需要用到维度转换函数，然而维度转换函数是复杂的，所以我们可以直接使用核函数，因为核函数就等于维度转换函数的点积结果。所以我们就可以根据原维度的点积结果直接计算出新维度的点积结果

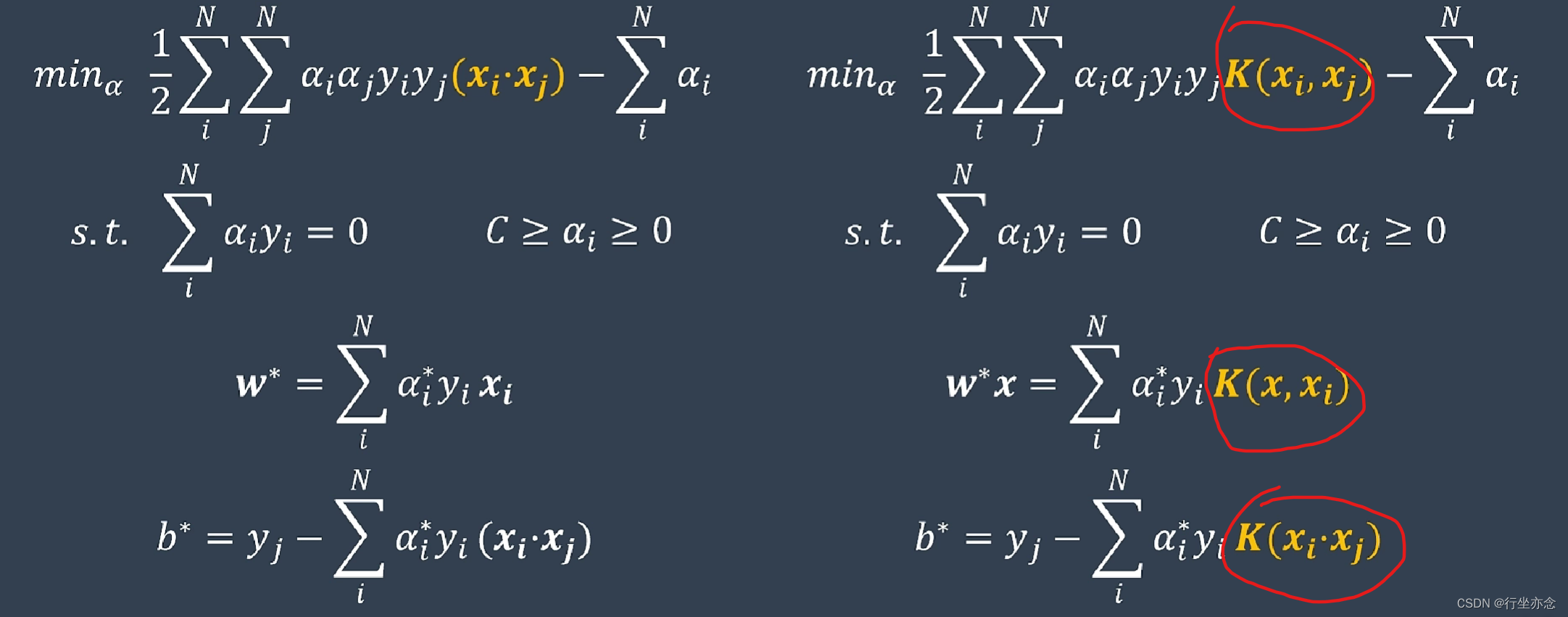
我们可以看到左边为软间隔对偶问题的优化结果，非线性支持向量机问题就是使用核函数代替点积结果从而求出问题的最优解。

六、支持向量机优缺点：

支持向量机 (SVMs) 可用于以下监督学习算法: 分类, 回归和异常检测.

支持向量机的优势在于:

在高维空间中非常高效.
即使在数据维度比样本数量大的情况下仍然有效.
在决策函数（称为支持向量）中使用训练集的子集,因此它也是高效利用内存的.
通用性: 不同的核函数核函数与特定的决策函数一一对应.常见的 kernel 已经提供,也可以指定定制的内核.

支持向量机的缺点包括:

如果特征数量比样本数量大得多,在选择核函数核函数时要避免过拟合, 而且正则化项是非常重要的.
计算复杂度高，支持向量机不直接提供概率估计,这些都是使用昂贵的五次交叉验算计算的. 所以在训练的过程中会非常耗时。

下面使用一个简单的例子使用支持向量机给鸢尾花数据集做分类：

假设我们有一个关于鸢尾花（Iris）数据集的问题，我们想要根据花瓣的长度和宽度来预测花的种类。为了简化，我们只考虑Setosa和Versicolour两种花，并将问题转化为一个二分类问题。

数据加载：

from sklearn import datasets  
from sklearn.model_selection import train_test_split  
from sklearn.preprocessing import StandardScaler  # 加载Iris数据集  
iris = datasets.load_iris()  
# 仅保留Setosa和Versicolour的样本  
X = iris.data[(iris.target == 0) | (iris.target == 1)][:, :2]  # 仅使用花瓣长度和宽度  
y = (iris.target[(iris.target == 0) | (iris.target == 1)] == 0).astype(int)  # 将目标转换为0和1  # 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  # 特征缩放  
scaler = StandardScaler()  
X_train = scaler.fit_transform(X_train)  
X_test = scaler.transform(X_test)

使用SVM训练模型：

from sklearn import svm  # 创建SVM分类器对象  
clf = svm.SVC(kernel='linear', C=1.0, random_state=42)  # 训练模型  
clf.fit(X_train, y_train)

对模型进行预测和评估：

from sklearn.metrics import accuracy_score  # 预测测试集的结果  
y_pred = clf.predict(X_test)  # 计算准确率  
accuracy = accuracy_score(y_test, y_pred)  
print(f"Accuracy: {accuracy}")

七、总结：

支持向量机（SVM）的功能强大，通过不同类别的数据点以最大间隔的超平面来实现分类，适用性也很普遍，区分硬间隔与软间隔以及非线性支持向量机，硬间隔也就是数据点是线性可分的情况下优化出的结果，软间隔则是硬间隔的基础上多了几个混乱的数据点，根据计算这些混乱数据点的影响则是引入了松弛变量（我叫它损失函数），非线性支持向量则是当数据点无法进行分类时候将数据从原始空间映射到一个更高维的特征空间从而实现分类。
（以上为自学笔记，侵删。）