前言:
Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。
本篇博客讲解朴素Dijkstra算法,第二篇博客讲解堆优化Dijkstra算法Dijkstra求最短路篇二(全网最详细讲解两种方法,适合小白)(python,其他语言也适用),两中算法思路大体相同,但时间复杂度有所区别。
- 朴素Dijkstra算法:时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 堆优化Dijkstra算法:时间复杂度 O ( m l o g n ) O(mlogn) O(mlogn)
两篇博客给出的题目内容一样,只有数据规模不一样。
题目:
题目链接:
849. Dijkstra求最短路 I
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围(两题不同处)
1 ≤ n ≤ 500 1≤n≤500 1≤n≤500,
1 ≤ m ≤ 1 0 5 1≤m≤10^5 1≤m≤105。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
Dijkstra算法介绍:
Dijkstra求最短路问题是图论的经典问题,首先介绍一下Dijkstra算法的流程图:
迪杰斯特拉算法采用的是一种贪心的策略。
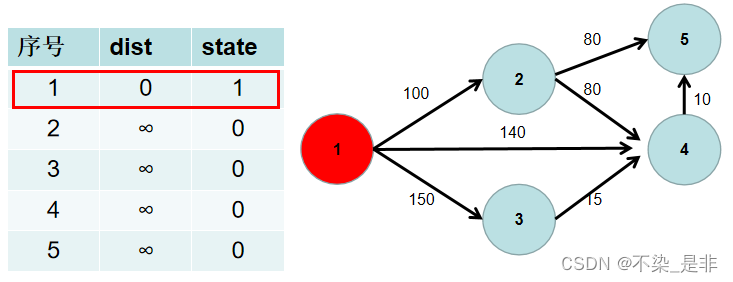
求源点到其余各点的最短距离步骤如下:
- 用一个 dist 数组保存源点到其余各个节点的距离,dist[i] 表示源点到节点 i 的距离。初始时,dist数组的各个元素为无穷大。
用一个状态数组 state 记录是否找到了源点到该节点的最短距离,state[i] 如果为真,则表示找到了源点到节点 i 的最短距离,state[i] 如果为假,则表示源点到节点 i 的最短距离还没有找到。初始时,state 各个元素为假。
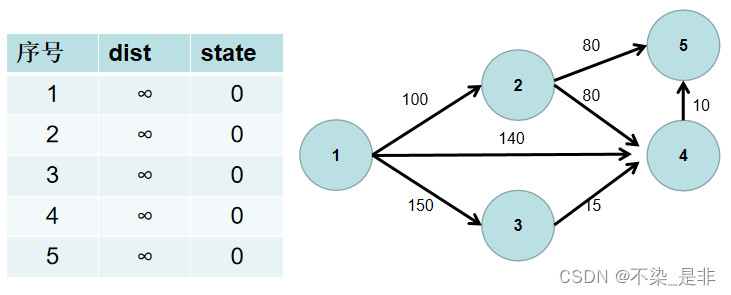
- 源点到源点的距离为 0。即dist[1] = 0。
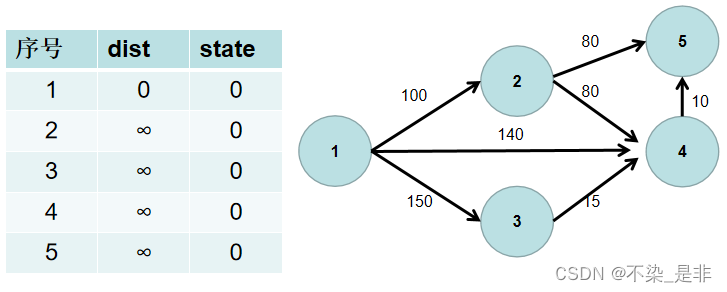
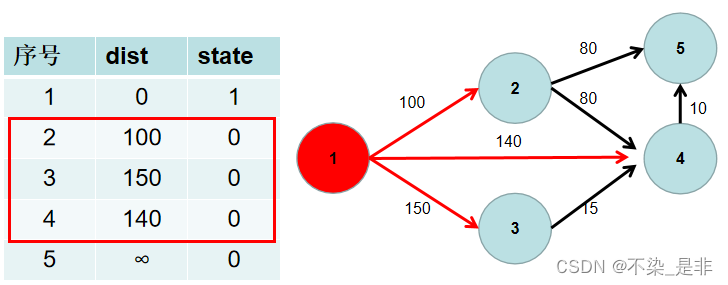
- 遍历 dist 数组,找到一个节点,这个节点是:没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离,state[i] 置为 1。
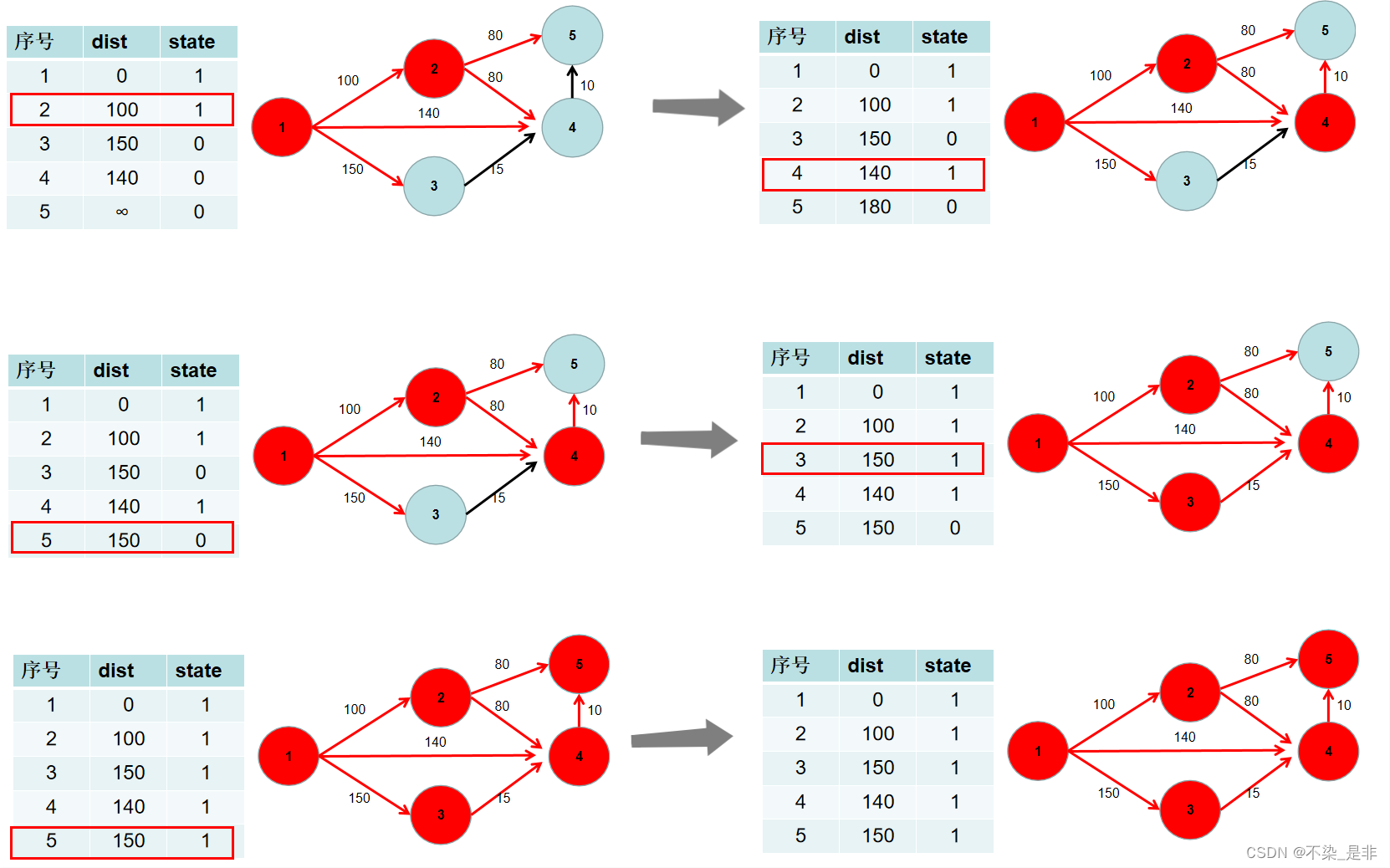
- 遍历 i 所有可以到达的节点 j,如果 dist[j] 大于 dist[i] 加上 i -> j 的距离,即 dist[j] > dist[i] + w[i][j](w[i][j] 为 i -> j 的距离) ,则更新 dist[j] = dist[i] + w[i][j]。
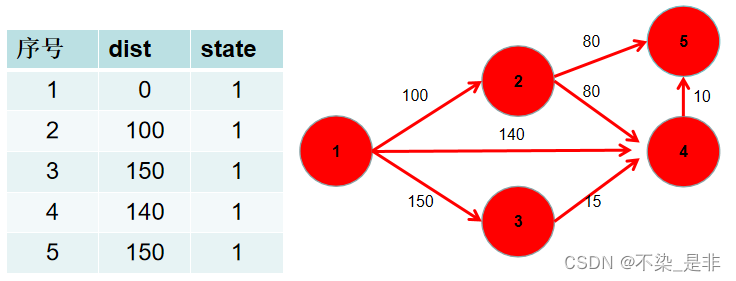
- 重复 3 4 步骤,直到所有节点的状态都被置为 1。
- 此时 dist 数组中,就保存了源点到其余各个节点的最短距离。
思路:
首先对数据进行存储,图的存储有两种方式,一种是邻接表,一种是邻接矩阵。题目中的数据规模用邻接矩阵存储(本题数据规模是稠密图,更省空间)。
为什么要用邻接矩阵去存贮,而不是邻接表?
我们采用邻接矩阵还是采用邻接表来表示图,需要判断一个图是稀疏图还是稠密图。稠密图指的是边的条数|E|接近于|V|²,稀疏图是指边的条数|E|远小于于|V|²(数量级差很多)。本题是稠密图,显然稠密图用邻接矩阵存储比较节省空间,反之用邻接表存储。
这里需要注意的是,题目中指出图中可能存在重边和自环。
- 重环是指两个点之间有多条边,每个边的距离不同。
- 自环是指一个点存在一条连向自己的边。
所以为了解决重环和自环问题,存储过程中需要存距离的最小值
邻接矩阵存储代码如下:
n, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接矩阵 float("inf")在python中是无限大的意思
num = [[float("inf") for j in range(n + 1)] for i in range(n + 1)]
for i in range(m):a, b, c = map(int, input().split())num[a][b] = min(num[a][b], c)
以题目实例为例,打印num数组(这里存储的是有向边,所以不是关于对角线对称的):
[[inf, inf, inf, inf], [inf, inf, 2, 4], [inf, inf, inf, 1], [inf, inf, inf, inf]]
邻接矩阵构建完成之后就要进行Dijkstra算法,这里直接给出代码,用详细代码给大家进行讲解。
代码及详细注释:
n, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接矩阵 float("inf")在python中是无限大的意思
num = [[float("inf") for j in range(n + 1)] for i in range(n + 1)]
for i in range(m):a, b, c = map(int, input().split())num[a][b] = min(num[a][b], c)
dist = [float('inf') for _ in range(n + 1)] # dist 数组用于记录每一个点距离第一个点的距离
dist[1] = 0 # 源点到源点的距离为置为 0
state = [False for _ in range(n + 1)] # state 用于记录该点的最短距离是否已经确定def dijkstra():for i in range(n): # 有n个点所以要进行n次迭代 (这里迭代多了并不影响结果,因为有state数组来记录每个点的状态)t = -1 # 该点不唯一,只要是在n个节点之外或者是最后一个节点就行(也可以是0,-1表示最后一个节点)for j in range(1, n + 1): # 循环每个点,找到最短距离的点,并把它赋值给t,(j表示各个节点)if not state[j] and dist[j] < dist[t]: # 该点未找到最短距离,且j点到第一个点的距离小于t点到第一个点的距离t = jstate[t] = True # 标记该点距离确定for j in range(1, n + 1): # # 根据该点更新其他所有点的距离dist[j] = min(dist[j], dist[t] + num[t][j])# 判断最后一个点的最短距离是否找到,如果为无穷大,则表示未找到,返回-1,否则返回最短距离dist[-1]if dist[n] == float('inf'):return -1else:return dist[-1]print(dijkstra())代码看着稍微复杂点,但拿实例数据跟着过一遍就一目了然。
这里拿实例带大家过一遍:
- 首先进行迭代,给t赋值为最后一个点(点3)的索引(索引值为-1,写n也可以)。之后循环这三个点,只有点1的dist距离(0)是小于最后一个点的dist值的(无穷大),所以 state[1] = True,然后循环所有的点,更新所有点到源点(点1始终是源点)的距离,dist[2] = 2, dist[3] = 4(点1与点2和点3直接相连,直接更新当前距离即可)
- 然后给t重新赋值为-1(这点很关键,不然之后都是跟点1进行比较了,算不出结果)。循环所有点后发现只有点2dist距离(2)是小于最后一个点的dist距离的(4)(点1的state为True,也就是已经找到最短距离了,不参与其中),之后都是重复第一步操作,更新dist[3] = 3
- 再一次循环时未更新值,只是把state[3] = True 的最短距离更新了,之后就会输出结果3
下面也会对大家难以理解的问题进行讲解回答(重点!!!):
t为什么要赋值为-1?
答:由于每一次都要找到还没有确定最短路距离的所有点中,距离当前的点最短的点(也就是始终为无穷大的值的点)。t = - 1是为了在st这个集合中找第一个点更新时候的方便所设定的(也可以是0,因为题目中不存在点0,但0的索引确始终存d在)。
- 为什么要进行n次迭代,dijkstra函数中
for i in range(n):的意义是什么?
答:这里的每次迭代主要是更新state数组的最短距离是否被找到,每一次迭代都会固定一个点的最短距离。
- 如果是问编号a到b的最短距离该怎么改呢?
初始化时 dist[a]=0, 以及返回时return dist[b]
- 为什么dist要初始化为无穷,邻接矩阵的部分点用无穷表示呢?
答:首先对于邻接矩阵而言,存储的是两点之间边的距离,如果两点之间不存在边,那肯定用无穷大来表示到达不了,dist数组初始化无穷大是因为这里要求最短路径,需要初始化一个较大值,这里初始化无穷大以免出错。
总结:
朴素版dijkstra适合稠密图
思路:
集合S为已经确定最短路径的点集。
- 初始化距离 一号结点的距离为零,其他结点的距离设为无穷大(看具体的题)。
- 循环n次,每一次将集合S之外距离最短X的点加入到S中去(这里的距离最短指的是距离1号点最近。 点X的路径一定最短,基于贪心,严格证明待看)。然后用点X更新X邻接点的距离。
时间复杂度分析:
- 寻找路径最短的点: O ( n 2 ) O(n^2) O(n2)
- 加入集合S: O ( n ) O(n) O(n)
- 更新距离: O ( m ) O(m) O(m)
- 所以总的时间复杂度为 O ( n 2 ) O(n^2) O(n2)