排序（前篇）

1.排序的概念及其运用

2.插入排序的概念及实现

3.希尔排序的概念及实现 

4.选择排序概念及实现

总代码（对比各个排序在大量的数据情况排序所化的时间）：

1.排序的概念及其运用

1.1排序的概念


排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次
序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不断地在内外存之间移动数据的排序。

1.2排序的运用

在网上购物时，会出现综合，销量及评论数等，会以此为参考来排序，选出综合最高，销量最高的产品，以及院校排名这些，都使用了排序。

（以下图片仅参考）

1.3 常见的排序算法

2.插入排序的概念及实现

2.1插入排序的概念

就像扑克牌一样，每拿到一张牌都要放进已经排好序的牌里面，用这张牌跟里面的比较，再把这张牌放到合适的位置，插入排序的原理就是把数插入已经排好序的数里面，比较排好数的里面的每一个数，找到位置就插入。

代码：

#include<stdio.h>
void InsertSort(int* a,int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end+1];while (end >= 0){if (tmp < a[end]){a[end+1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
int main()
{int a[10] = { 3,4,5,1,2,6,7,8,2 };int size = sizeof(a) / sizeof(a[0]);InsertSort(a,size);for (int i = 0; i < 9; i++){printf("%d ", a[i]);}return 0;
}

代码分析： 

while循环出去有俩种情况，1是触发break，二是while循环的条件不满足，在循环外把tmp赋给数组下标为end+1的位置， 是因为如果是while循环结束的话刚好也可以赋值，但是在里面的话，因为while结束的就无法把数据加回去（移动带来覆盖，会有一位重复，需要赋值来填回去）。

（动态图关于插入排序24年-05月27日--排序/动图/插入排序.gif · 比特杭哥/113期 - Gitee.com）

2.2冒牌排序的时间复杂度

冒泡排序的最坏情况：

假设if条件每次都会执行，那么时间复杂度就为O(N^2).

最好的情况：

上面冒泡代码不能做到O(N),需要对其优化才能使冒泡排序达到最好情况，

设置一个flag去判断是否触发了if条件，如果触发了就置为0，后面再去检验值是否为一开始的初始值，是就说明没有触发if条件，没触发就说明顺序是排好的，只执行了里面的if判断，所以时间复杂度是O(N)。

void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){int flag = 1;for (int j = 0; j < n-i-1; j++){if (a[j] > a[j + 1]){int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;flag = 0;}}if (flag == 1){break;}}
}

2.3插入排序的时间复杂度

按照最坏打算：

既逆序情况

最好的情况：

当数据是以升序排序时，里面的循环不执行（会从break跳出），则只有for循环执行，所以时间复杂度就为O(N)。

插入排序与冒泡排序的时间复杂度虽然是一样的，但插入排序是比冒泡排序好，因为插入排序最坏的情况很难达到，只有是逆序（或者接近这个情况）的情况下，插入排序才会慢下来，而冒泡排序一般都是O(N^2),因为冒泡每次遍历选出其中最大的放最后，if的条件任意触发。

void BubbleSort(int* a, int n)//冒泡排序
{for (int i = 0; i < n; i++){for (int j = 0; j < n-i-1; j++){if (a[j] > a[j + 1]){int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;}}}
}

3.希尔排序的概念及实现 

3.1希尔排序概念

希尔排序与插入排序密不可分，基于插入排序来实现希尔排序的。

希尔排序：首先会对数据进行预排序（让数组接近有序），再进行插入排序（因为插入排序怕的是数组是逆序情况）。

预排序：把数组在逻辑上分成gap组，gap是间隔的距离，然后对每个gap组进行插入排序，这样可以使大的数据跑到比较后面的位置，小的数据会跑到比较前面的位置，gap设置的越大，大的数据越快到后面，小的数据越快到前面，越不接近有序，gap设置的越小，数据跳的慢，但是会越接近有序的情况，gap为1的时候就是插入排序了，希尔排序就是慢慢把gap的值调小（设置gap是为了最后一次gap为一做铺垫，为了插入排序能更快的完成），最后gap为一时执行插入排序。

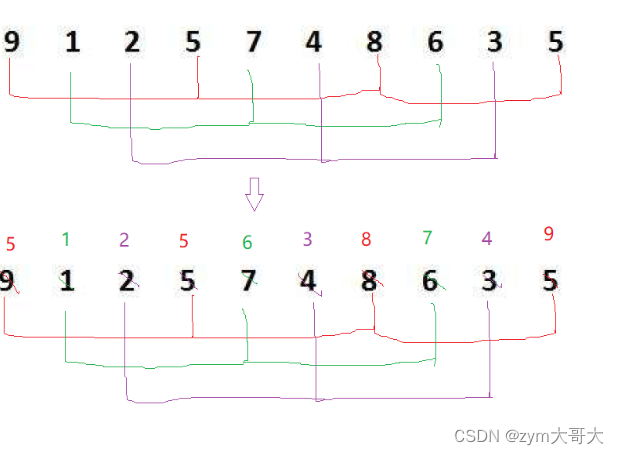
3.2希尔排序的代码实现

代码实现1：

void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
void ShellSort1(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){swap(&a[end], &a[end + gap]);end-=gap;}elsebreak;}a[end + gap] = tmp;}}
}

代码实现二：

void ShellSort2(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){swap(&a[end], &a[end + gap]);end -= gap;}elsebreak;}a[end + gap] = tmp;}}}
}

代码分析：上面俩个代码的样子不一样，但是效率是一样的俩种都可以使用，

n是数组的个数，一般gap的值都为个数的三分之一+1，加一是为了最后gap的值能达到一进行插入排序，gap/2的效率不如gap/3（大量数据实验得出的），代码一是多个gap组同时进行预排序，每次i加一，但是比的是gap距离的数据，gap第一组的第一个跟其gap距离的比完后，第二个gap组的第一个跟其gap距离的比，再到第三个gap组的第一个与其gap距离的数据比较，再到第二个等等，代码二则是第一个gap组会一直比完才到第二个gap组比。还需要注意的是循环终止条件是n-gap，是因为循环里面有end+gap，n+gap-gap刚好是为n，也就是数组最后一个数据下标的下一个，有效数据的下一个是不能访问的，会造成越界访问，数组最多能访问到n-1的位置，如果是i<n，则a[end+gap]就会越界了。

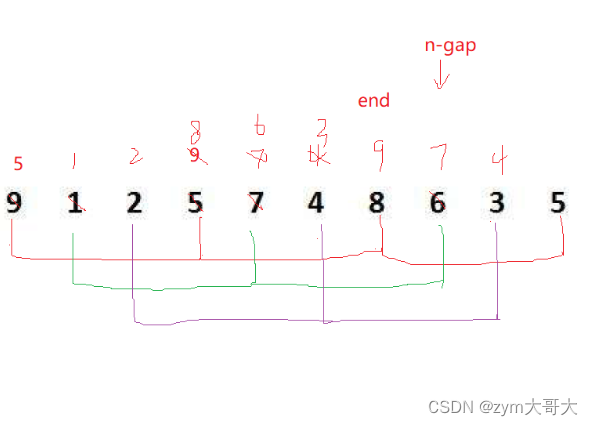
3.3希尔排序的时间复杂度（简单分析）

希尔排序的时间复杂度为O(N^1.3)。

4.选择排序概念及实现

选择排序就是遍历数组找到最小的数据并把它放在最前面，可以对它进行优化，就是在遍历的同时把最大和最小的数据找出来并放在俩边

代码实现：

void SelectSort(int* a, int n)
{int begin, end;begin = 0;end = n - 1;while (begin < end){int mini, max;mini = max = begin;for (int i = begin+1; i <= end; i++){if (a[mini] > a[i]){mini = i;}if (a[max] < a[i]){max = i;}}swap(&a[mini], &a[begin]);if(begin==max){max=mini;}swap(&a[max], &a[end]);end--;begin++;}	
}

代码分析：

因为是找最大和最小并放在俩边，所以begin和end会慢慢往中间靠近，在定义最小值和最大值去和数组的每一个数比较，比定义的最大值大就交换一下下标，比最小值小就交换 下标，遍历完后在交换值，并且把begin++和end--，因为begin和end都放好了对应的值，要放其它位置的值。

总代码（对比各个排序在大量的数据情况排序所化的时间）：

test.c文件：

#include"Sort.h"void TestInsertSort()
{int a[] = { 2,4,1,7,8,3,9,2 };InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestShellSort()
{int a[] = { 9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5 };//InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));ShellSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestSelectSort()
{//int a[] = { 9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5,9,1,2,5,7,4,6,3,5 };//InsertSort(a, sizeof(a) / sizeof(int));//int a[] = { 2,4,1,7,8,3,9,2 };int a[] = { 9,1,2,5,7,4,6,3 };PrintArray(a, sizeof(a) / sizeof(int));SelectSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestOP()
{srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand()+i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();//InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();//SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();//QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();//MergeSort(a6, N);int end6 = clock();int begin7 = clock();//BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//TestInsertSort();//TestShellSort();TestSelectSort();//TestOP();return 0;
}

Sort.h文件：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<time.h>void PrintArray(int* a, int n);// 有实践意义
void InsertSort(int* a, int n);void ShellSort(int* a, int n);void ShellSort(int* a, int n);void HeapSort(int* a, int n);// 适合教学，实践中没啥价值
void BubbleSort(int* a, int n);void SelectSort(int* a, int n)

Sort.c文件：

#include"Sort.h"void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 时间复杂度：O(N^2)  什么情况最坏：逆序
// 最好：顺序有序，O(N)
// 插入排序
void InsertSort(int* a, int n)
{//  [0, n-1]for (int i = 0; i < n - 1; i++){// [0, n-2]是最后一组// [0,end]有序 end+1位置的值插入[0,end]，保持有序int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}// O(N^1.3)
//void ShellSort(int* a, int n)
//{
//	/*int gap = 3;
//	for (int j = 0; j < gap; j++)
//	{
//		for (size_t i = j; i < n - gap; i += gap)
//		{
//			int end = i;
//			int tmp = a[end + gap];
//			while (end >= 0)
//			{
//				if (tmp < a[end])
//				{
//					a[end + gap] = a[end];
//					end -= gap;
//				}
//				else
//				{
//					break;
//				}
//			}
//			a[end + gap] = tmp;
//		}
//	}*/
//
//	int gap = n;
//	while (gap > 1)
//	{
//		// +1保证最后一个gap一定是1
//		// gap > 1时是预排序
//		// gap == 1时是插入排序
//		gap = gap / 3 + 1;
//
//		for (size_t i = 0; i < n - gap; ++i)
//		{
//			int end = i;
//			int tmp = a[end + gap];
//			while (end >= 0)
//			{
//				if (tmp < a[end])
//				{
//					a[end + gap] = a[end];
//					end -= gap;
//				}
//				else
//				{
//					break;
//				}
//			}
//			a[end + gap] = tmp;
//		}
//		//printf("gap:%2d->", gap);
//		//PrintArray(a, n);
//	}
//}// O(N ^ 1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){// +1保证最后一个gap一定是1// gap > 1时是预排序// gap == 1时是插入排序gap = gap / 3 + 1;for (size_t i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}void AdjustDown(int* a, int n, int parent)
{// 先假设左孩子小int child = parent * 2 + 1;while (child < n)  // child >= n说明孩子不存在，调整到叶子了{// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{// 向下调整建堆 O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}// O(N^2) 最坏
// O(N)   最好
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){// 单趟int flag = 0;for (int i = 1; i < n - j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);flag = 1;}}if (flag == 0){break;}}
}void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);++begin;--end;}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/341700.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

纯血鸿蒙开发教程：如何实现运动饮食卡片效果

纯血鸿蒙开发教程：如何实现运动饮食卡片效果

开发背景 人们对健康的要求越来越高&#xff0c;从单纯的健康饮食到健康运动&#xff0c;再到两者的结合。但是&#xff0c;饮食和运动之间的平衡一般人很难掌握&#xff0c;而我们这款 APP 将饮食、运动、以及自身身体状况&#xff08;如体脂、体重、内脂等&#xff09;有机结…
阅读更多...
保护关键业务资产的四个步骤

保护关键业务资产的四个步骤

提到 “关键资产 ”&#xff0c;相信大家并不陌生&#xff0c;它是企业 IT 基础设施中对组织运作至关重要的技术资产。如果这些资产&#xff08;如应用服务器、数据库或特权身份&#xff09;出现问题&#xff0c;势必会对企业安全态势造成严重影响。 但每项技术资产都被视为关…
阅读更多...
2024年大屏幕互动源码+动态背景图和配乐素材+搭建教程

2024年大屏幕互动源码+动态背景图和配乐素材+搭建教程

2024年大屏幕互动源码动态背景图和配乐素材搭建教程 php宝塔搭建部署活动现场大屏幕互动系统php源码 运行环境&#xff1a;PHPMYSQL 下载源码地址&#xff1a;极速云
阅读更多...
[AI资讯·0605] GLM-4系列开源模型，OpenAI安全疑云，ARM推出终端计算子系统，猿辅导大模型备案……

[AI资讯·0605] GLM-4系列开源模型，OpenAI安全疑云，ARM推出终端计算子系统，猿辅导大模型备案……

AI资讯 1毛钱1百万token&#xff0c;写2遍红楼梦&#xff01;国产大模型下一步还想卷什么&#xff1f;AI「末日」突然来临&#xff0c;公司同事集体变蠢&#xff01;只因四大聊天机器人同时宕机OpenAI员工们开始反抗了&#xff01;AI手机PC大爆发&#xff0c;Arm从软硬件到生态…
阅读更多...
React + Taro 项目 实际书写 感受

React + Taro 项目 实际书写 感受

之前我总结了部分react 基础 根据官网的内容 以及Taro 框架的内容 今天我试着开始写了一下页面和开发 说一下我的感受 我之前写的是vue3 今天是第一次真正根据需求做页面开发 和逻辑功能 代码的书写 主体就是开发了这个页面 虽说这个页面 很简单 但是如果你要是第一次写 难说…
阅读更多...
【设计模式】结构型-组合模式

【设计模式】结构型-组合模式

前言 在软件开发中&#xff0c;设计模式是一种被广泛应用的解决问题的方法论。其中&#xff0c;结构性设计模式是一类特别重要的模式&#xff0c;它们用于处理类或对象之间的组合关系&#xff0c;其中之一就是组合模式。组合模式允许客户端统一对待单个对象和对象的组合&#…
阅读更多...
使用cesiumLab使shp转为3dtlies

使用cesiumLab使shp转为3dtlies

过程不做赘述&#xff0c;网上大把&#xff0c;说下注意事项。 1. 存储3DTiles 选项 若是打开则输出的文件为glb格式文件,因为glb文件好储存易传输跨平台。cesium可以使用但无法处理&#xff0c;例如改变颜色&#xff0c;改着色器等。若是不打开则输出的文件为bm3d格式文件,此…
阅读更多...
二叉树—堆（C语言实现）

二叉树—堆（C语言实现）

一、树的概念及结构 1.树的概念 树是一种非线性的数据结构&#xff0c;它是有n&#xff08;n > 0&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下。 ● 有一个特殊的结点…
阅读更多...
C++设计模式-单例模式，反汇编

C++设计模式-单例模式，反汇编

文章目录 25. 单例模式25.1. 饿汉式单例模式25.2. 懒汉式单例模式25.2.1. 解决方案125.2.2. 解决方案2 &#xff08;推荐写法&#xff09; 运行在VS2022&#xff0c;x86&#xff0c;Debug下。 25. 单例模式 单例即该类只能有一个实例。 应用&#xff1a;如在游戏开发中&#x…
阅读更多...
搭建大型分布式服务（三十九）SpringBoot 整合多个kafka数据源-支持Aware模式

搭建大型分布式服务（三十九）SpringBoot 整合多个kafka数据源-支持Aware模式

系列文章目录 文章目录 系列文章目录前言一、本文要点二、开发环境三、原项目四、修改项目五、测试一下五、小结 前言 本插件稳定运行上百个kafka项目&#xff0c;每天处理上亿级的数据的精简小插件&#xff0c;快速上手。 <dependency><groupId>io.github.vipjo…
阅读更多...
算法第三天力扣第69题：X的平方根

算法第三天力扣第69题：X的平方根

69. x 的平方根 (可点击下面链接或复制网址进行做题) https://leetcode.cn/problems/sqrtx/https://leetcode.cn/problems/sqrtx/ 给你一个非负整数 x &#xff0c;计算并返回 x 的 算术平方根 。 由于返回类型是整数&#xff0c;结果只保留 整数部分 &#xff0c;小数部分将被…
阅读更多...
SpringBoot的第二大核心AOP系统梳理

SpringBoot的第二大核心AOP系统梳理

目录 1 事务管理 1.1 事务 1.2 Transactional注解 1.2.1 rollbackFor 1.2.2 propagation 2 AOP 基础 2.1 AOP入门 2.2 AOP核心概念 3. AOP进阶 3.1 通知类型 3.2 通知顺序 3.3 切入点表达式 execution切入点表达式 annotion注解 3.4 连接点 1 事务管理 1.1 事务…
阅读更多...
【踏雪无痕的痕六】——数学中有意思的问题

【踏雪无痕的痕六】——数学中有意思的问题

一、背景介绍 提出一个问题往往比解决一个问题更有意义&#xff0c;因为提出一个问题相当于提出了一个思考问题的维度&#xff1b;而解决一个问题是沿着这个维度将已有的知识串起来的过程 三、过程 1.数人数你会吗&#xff1f; 小名再第10位&#xff0c;小李再第15位&#…
阅读更多...
【源码】Spring Data JPA原理解析之Repository自定义方法命名规则执行原理（二）

【源码】Spring Data JPA原理解析之Repository自定义方法命名规则执行原理（二）

Spring Data JPA系列 1、SpringBoot集成JPA及基本使用 2、Spring Data JPA Criteria查询、部分字段查询 3、Spring Data JPA数据批量插入、批量更新真的用对了吗 4、Spring Data JPA的一对一、LazyInitializationException异常、一对多、多对多操作 5、Spring Data JPA自定…
阅读更多...
位运算算法

位运算算法

位运算是计算机中常用的一种运算方法&#xff0c;它直接对二进制数的位进行操作。位运算主要包括按位与&#xff08;&&#xff09;、按位或&#xff08;|&#xff09;、按位异或&#xff08;^&#xff09;、按位取反&#xff08;~&#xff09;、左移&#xff08;<<&a…
阅读更多...
【云原生】Kubernetes----Ingress对外服务

【云原生】Kubernetes----Ingress对外服务

目录 引言 一、K8S对外方式 &#xff08;一&#xff09;NodePort 1.作用 2.弊端 3.示例 &#xff08;二&#xff09;externalIPs 1.作用 2.弊端 3.示例 &#xff08;三&#xff09;LoadBalancer 1.作用 2.弊端 &#xff08;四&#xff09;Ingress 二、Ingress的…
阅读更多...
ChatGPT-4o抢先体验

ChatGPT-4o抢先体验

速度很快&#xff0c;结果很智能&#xff0c;支持多模态输入输出&#xff0c;感兴趣联系作者。 windows/linux/mac 客户端下载参考&#xff1a;https://github.com/lencx/Noi
阅读更多...
dns域名解析服务和bond网卡

dns域名解析服务和bond网卡

目录 dns域名解析服务 一、DNS 1、定义 2、以www.baidu.com为例 3、域名体系结构 4、DNS解析使用的协议和端口 5、dns域名解析的过程 6、dns解析的优先级 二、如何实现域名解析 1、域名解析 2、bind配置文件位置 &#xff08;一&#xff09;正向解析 &#xff08;…
阅读更多...
IP协议1.0

IP协议1.0

基本概念&#xff1a; • 主机: 配有IP地址, 但是不进⾏路由控制的设备; • 路由器: 即配有IP地址, ⼜能进⾏路由控制; • 节点: 主机和路由器的统称; IP协议的报头 • 4位版本号(version): 指定IP协议的版本, 对于IPv4来说, 就是4. • 4位头部⻓度(header length): IP头部的⻓…
阅读更多...
高并发系统限流原理

高并发系统限流原理

短时间内巨大的访问流量&#xff0c;我们如何让系统在处理高并发的同时还能保证自身系统的稳定性&#xff1f;估计有人会说&#xff0c;增加机器就可以了&#xff0c;因为我的系统架构设计就是按照分布式思想进行架构设计的&#xff0c;所以可以只需要增加机器就可以解决问题了…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023