知乎三角猫frank对于这块内容写的非常好,但这个输入的构造还是很难过于没头没尾
数学好的人,可能看一眼根据形式就能推出gramian的构造,但对我这种比较钻牛角尖的人,我就想有一个逻辑链条——gramian是怎么被构造出来的?
我们回到问题本身,就以能控性为例子(和上面的rechability不太一样)
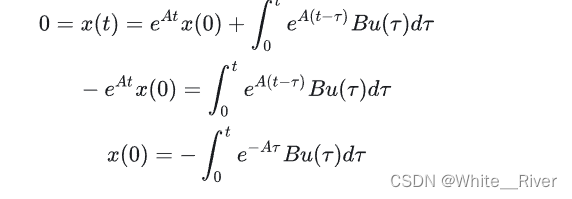
这里的 x ( 0 ) x(0) x(0)是任意一个n维的向量 我们想找一个条件,让这个等式成立
也就是找一个可控的充分条件
显然我们只能从 u ( τ ) u(\tau) u(τ)下手,通过构造适当的 u ( τ ) u(\tau) u(τ),让系统能够回到零状态,也就是能控
对于控制输入,我们知道自动控制里 要么是开环 要么是闭环
对于一般的系统,我们先尝试用状态反馈进行闭环控制
如果是闭环,那么控制输入 u m × 1 u_{m\times 1} um×1应该长成这样
u ( τ ) = u ( τ , x ) = u ( τ , x ( τ ) ) u(\tau) = u(\tau,x) = u(\tau,x(\tau)) u(τ)=u(τ,x)=u(τ,x(τ))
因此状态反馈的输入可以尝试用
u ( τ ) = − A x ( τ ) u(\tau) = -Ax(\tau) u(τ)=−Ax(τ)
或者
u ( τ ) = − e A τ x ( τ ) u(\tau) = -e^{A\tau}x(\tau) u(τ)=−eAτx(τ)
但是这样维数对不上, u ( τ ) = − A x ( τ ) u(\tau) = -Ax(\tau) u(τ)=−Ax(τ) 是 n × 1 n\times 1 n×1的向量
因此你可能会想引入 B n × m B_{n \times m} Bn×m
让输入变成一个 m × 1 m\times 1 m×1的向量
也就是
u ( τ ) = − B ∗ A x ( τ ) u(\tau) = -B^*Ax(\tau) u(τ)=−B∗Ax(τ)
或者
u ( τ ) = − B ∗ e A τ x ( τ ) u(\tau) = -B^*e^{A\tau}x(\tau) u(τ)=−B∗eAτx(τ)
既然你都转置了一个,那不如就
u ( τ ) = − B ∗ A ∗ x ( τ ) u(\tau) = -B^*A^*x(\tau) u(τ)=−B∗A∗x(τ)
或者
u ( τ ) = − B ∗ e A ∗ τ x ( τ ) u(\tau) = -B^*e^{A^*\tau}x(\tau) u(τ)=−B∗eA∗τx(τ)
那干脆就用 u ( τ ) = − B ∗ e A ∗ τ x ( τ ) u(\tau) = -B^*e^{A^*\tau}x(\tau) u(τ)=−B∗eA∗τx(τ)
x ( 0 ) = ∫ e − A τ B B ∗ e A ∗ τ x ( τ ) d τ x(0) = \int e^{-A\tau} BB^*e^{A^*\tau}x(\tau) d \tau x(0)=∫e−AτBB∗eA∗τx(τ)dτ
为了对称,不如写成
x ( 0 ) = ∫ e − A τ B B ∗ e − A ∗ τ x ( τ ) d τ x(0) = \int e^{-A\tau} BB^*e^{-A^*\tau}x(\tau) d \tau x(0)=∫e−AτBB∗e−A∗τx(τ)dτ
但这样有一个问题,你从这里的不出任何有用的结果
但如果视为开环控制 把 x ( τ ) x(\tau) x(τ)视为一个常向量 y y y
x ( 0 ) = ∫ e − A τ B B ∗ e − A ∗ τ y d τ = [ ∫ e − A τ B B ∗ e − A ∗ τ d τ ] y x(0) = \int e^{-A\tau} BB^*e^{-A^*\tau}y d \tau = [\int e^{-A\tau} BB^*e^{-A^*\tau} d \tau ] y x(0)=∫e−AτBB∗e−A∗τydτ=[∫e−AτBB∗e−A∗τdτ]y
由于 y y y是任取的,那我们现在就得到了一个充分条件(注意 必要性还得不到)
即如果 W = ∫ e − A τ B B ∗ e − A ∗ τ d τ W = \int e^{-A\tau} BB^*e^{-A^*\tau} d \tau W=∫e−AτBB∗e−A∗τdτ是一个非奇异矩阵( n × n n \times n n×n)
则系统可控
为什么叫它格拉姆矩阵
因为一般格拉姆矩阵就是长这个样子 先内积再积分
这个只是一个特定的格拉姆矩阵形式
ok,那么你得到了充分性条件,而这个条件的必要性竟然很容易验证
怎么验证呢…显然最常用的手段就是反证法(一般验证充分条件必要性的方法)
就是说,你假设可控,但这个你构造出来的格拉姆矩阵是奇异的,然后会导致矛盾,具体的就不说了,大家可以自己证明.
然后你发现真的矛盾,也就是说
你偶然间发现了一个可控性的充要条件,一篇TAC到手