62. 不同路径

题目

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

示例1

输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

思路分析

该问题可以用**深度优先搜索（DFS）**来解决。通过遍历每一条可能的路径，从起点到达终点时，路径数加一。DFS方法可以完整地遍历所有路径，但在大规模数据上效率较低。

拆解分析

DFS函数

void dfs(int **board, int nowCol, int nowRow, int *cnt, int m, int n) {if (nowCol == m - 1 && nowRow == n - 1) // 到达终点，路径+1{(*cnt)++;return;}board[nowCol][nowRow] = 1; // 经过的点标记下，防止重复访问if (nowCol + 1 < m && board[nowCol + 1][nowRow] == 0) // 能向下就向下{dfs(board, nowCol + 1, nowRow, cnt, m, n);}if (nowRow + 1 < n && board[nowCol][nowRow + 1] == 0) // 不能向下就向右{dfs(board, nowCol, nowRow + 1, cnt, m, n);}board[nowCol][nowRow] = 0; // 回溯后记得清除访问记录return;
}

主函数

int uniquePaths(int m, int n) {int res = 0;int nowCol = 0;int nowRow = 0;int **board = (int**)calloc(m, sizeof(int*));for (int i = 0; i < m; i++) {board[i] = (int*)calloc(n, sizeof(int));}// 深度优先dfs(board, nowCol, nowRow, &res, m, n);// 释放资源for (int i = 0; i < m; i++) {free(board[i]);}free(board);return res;
}

复杂度分析

时间复杂度：
- DFS会遍历所有可能的路径。对于 m x n 的网格，总共有 O(2^(m+n)) 条路径。因此，时间复杂度为 O(2^(m+n))，这在大规模网格上是不可行的。
空间复杂度：
- 由于需要一个 m x n 的网格来记录访问状态，因此空间复杂度为 O(m * n)。

结果

果然
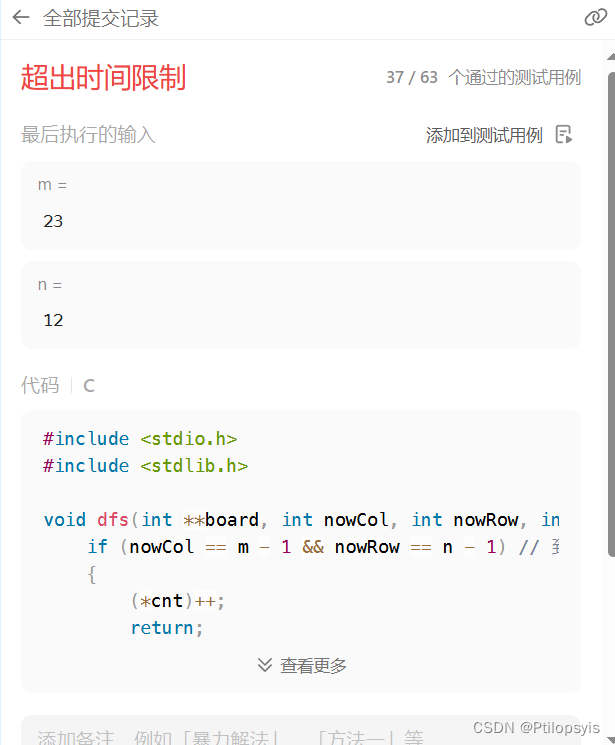
dfs算法结果

一题多解

动态规划

动态规划（DP）是该问题的最佳解法。通过构建一个 m x n 的 DP 表格来存储每个位置的路径数量，可以有效减少重复计算。

算法过程：
- 初始化DP表格，其中DP[0][0]为1（起点）。
- 每个位置的路径数量等于上方位置和左侧位置的路径数量之和。
- 最终结果存储在DP[m-1][n-1]中。

时间复杂度

动态规划 方法遍历了 m x n 的网格，每个网格点都需要进行常数时间的计算（加法）。
因此，时间复杂度为 O(m * n)。

空间复杂度

动态规划需要一个 m x n 的二维数组来存储中间结果。
因此，空间复杂度为 O(m * n)。

动态规划的代码示例

#include <stdio.h>
#include <stdlib.h>int uniquePaths(int m, int n) {int** dp = (int**)malloc(m * sizeof(int*));for (int i = 0; i < m; i++) {dp[i] = (int*)malloc(n * sizeof(int));}for (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int j = 0; j < n; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i-1][j] + dp[i][j-1];}}int result = dp[m-1][n-1];for (int i = 0; i < m; i++) {free(dp[i]);}free(dp);return result;
}

通过了

dp解法

数学法

另一个高效解法是使用组合数学。机器人从左上角到右下角，需要走 m-1 次向下和 n-1 次向右。因此，总路径数可以通过组合数计算，即 C(m+n-2, m-1) 或 C(m+n-2, n-1)。
数学法电脑用着快了，想出来的时间比较浪费[doge]

算法过程：
- 计算组合数 C(m+n-2, m-1)。
- 组合数计算公式：C(a, b) = a! / (b! * (a-b)!)。

时间复杂度

计算组合数 C(a, b) 需要进行 b 次乘法和除法操作，其中 a = m + n - 2 和 b = min(m-1, n-1)。
因此，时间复杂度为 O(min(m, n))。

空间复杂度

组合数学算法只使用了常数级别的额外空间。
因此，空间复杂度为 O(1)。

组合数学的代码示例

#include <stdio.h>long long combination(int a, int b) {if (b > a - b) b = a - b;long long result = 1;for (int i = 1; i <= b; i++) {result *= a - i + 1;result /= i;}return result;
}int uniquePaths(int m, int n) {return combination(m + n - 2, m - 1);
}