目录
- 0.何为背包问题?
- 1.模板 背包
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.分割等和子集
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
0.何为背包问题?
-
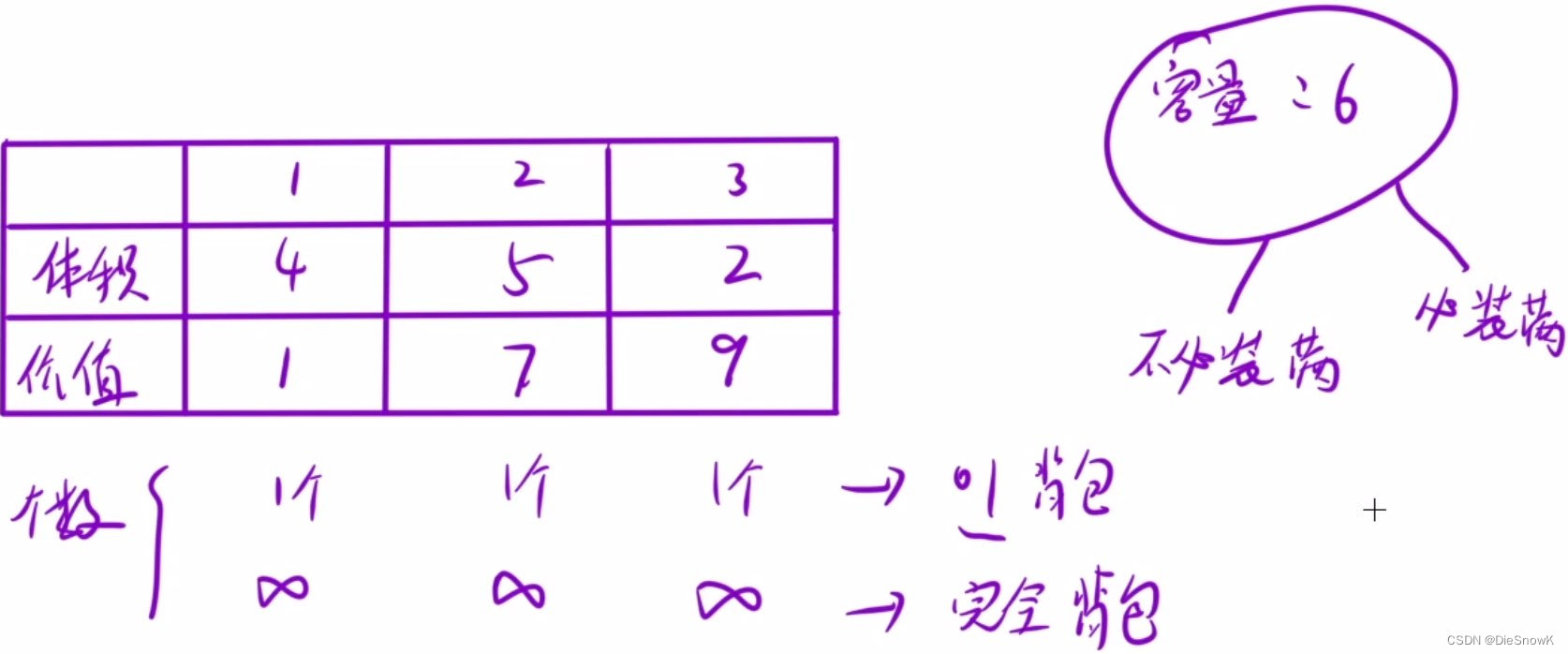
背包问题:有限制条件下的"组合问题"
-
你有一个背包,地上有一堆物品,挑选一些物品放入背包中
- 问:最大能挑选出来的价值是多少?
-
限制因素
- 物品的属性:价值等
- 背包的属性:容量大小等
- 背包是要求必装满还是不必装满?
-
当研究一个问题,出现选或者不选的情况,思路就可以往01背包上靠
-
注意:背包问题是必须要掌握的算法问题
1.模板 背包
1.题目链接
- [模板] 背包
2.算法原理详解
- 注意:01背包问题是所有背包问题的基础,此处的分析思路,可以用到很多题里面
- 思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]:从前i个物品中选,所有选法中,能挑选出来的最大价值 ×- 无法得知背包容量
- 不要求恰好装满
dp[i][j]:从前i个物品中挑选,总体积不超过j,所有选法中,能挑选出来的最大价值
- 要求恰好装满
dp[i][j]:从前i个物品中挑选,总体积恰好等于j,所有选法中,能挑选出来的最大价值
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
-
不要求恰好装满:
j - v[i] >= 0是为了确保背包此时容量足够塞下当前物品

-
要求恰好装满:
dp[i][j] == -1表示没有这种情况,即此时总体积凑不到j
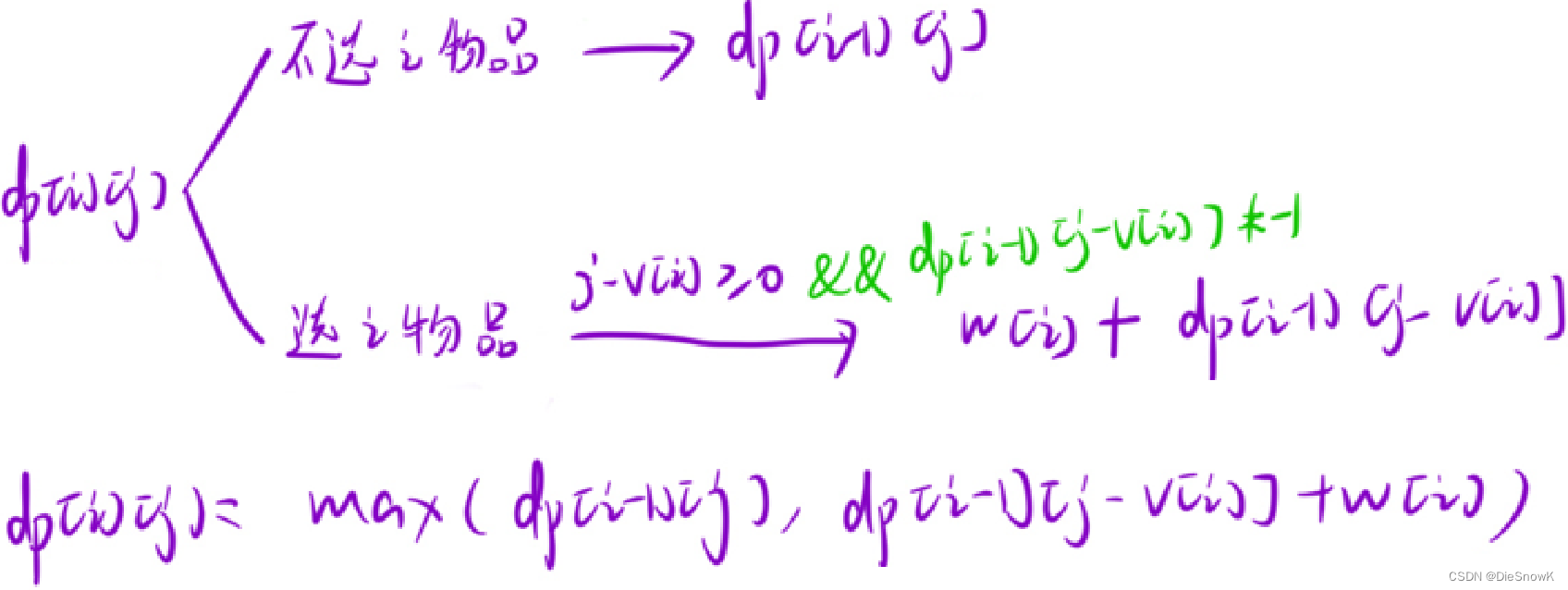
-
-
初始化:
- 不要求恰好装满:
vector<vector<int>> dp(n + 1, vector<int>(V + 1)) - 要求恰好装满:第一行除第一个位置,其余都为
-1
- 不要求恰好装满:
-
确定填表顺序:从上往下
-
确定返回值:
- 不要求恰好装满:
dp[n][V] - 要求恰好装满:
dp[n][V] == -1 ? 0 : dp[n][V]
- 不要求恰好装满:
-
- 滚动数组优化空间
-
每次填值,只依赖上一行的值
- 所以,理论上只需要两行一维数组,就可以解决问题
-
可以一个一维数组就优化掉此问题
- 但是如果从左往右遍历数组,会影响动态规划填值
- 因为原本的填值过程,会依赖左上方的值
- 此时,只需要从右往左遍历该数组,就不会影响动态规划的规程

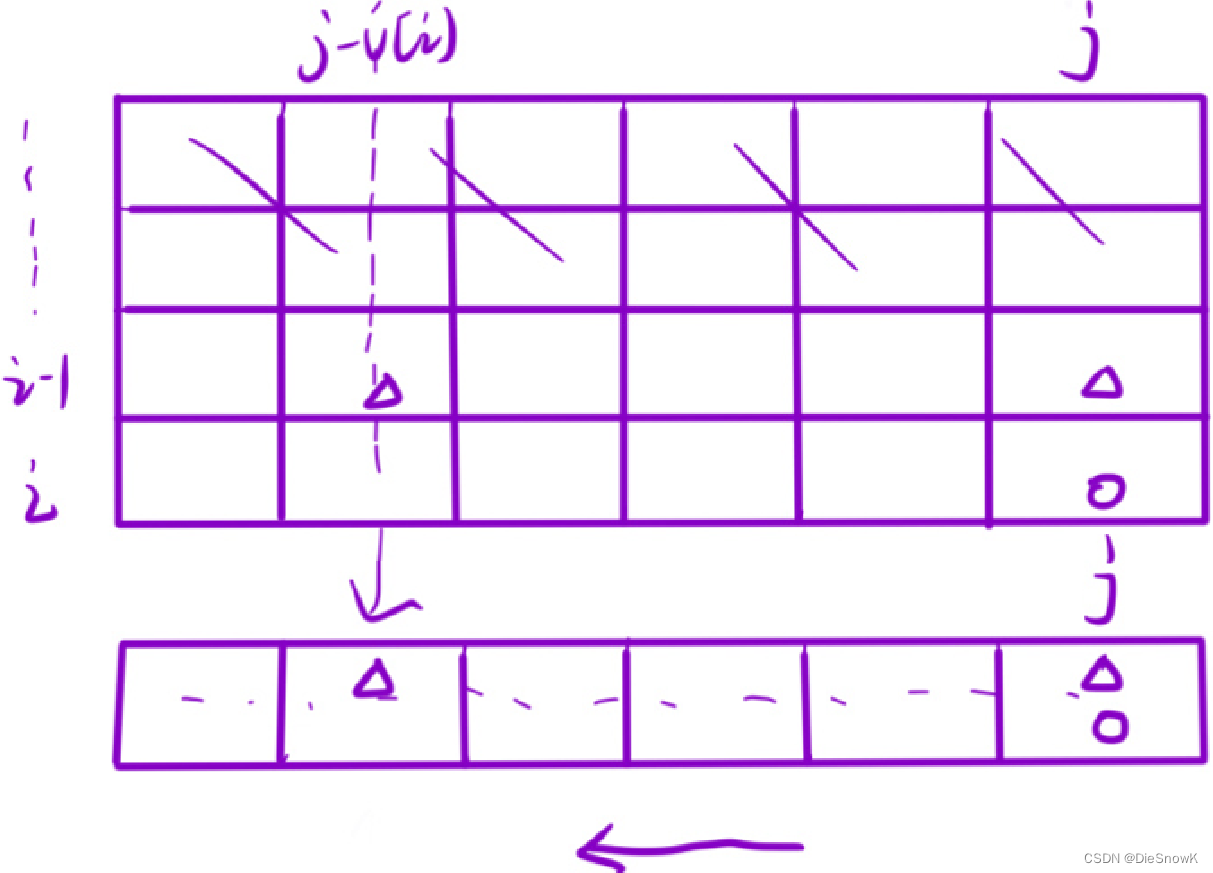
- 但是如果从左往右遍历数组,会影响动态规划填值
-
操作
- 删除所有的横坐标
- 修改一下
j的遍历顺序
-
注意:不要去强行解释优化后的妆台表示以及状态转移方程,费时费力还没啥意义
-
3.代码实现
// v1.0
int main()
{int n = 0, V = 0;cin >> n >> V;vector<int> v(n + 1), w(n + 1);for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}vector<vector<int>> dp(n + 1, vector<int>(V + 1));// Q1for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i]){dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}}cout << dp[n][V] << endl;// Q2dp.resize(n + 1, vector<int>(V + 1));for(int i = 1; i <= V; i++){dp[0][i] = -1;}for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i - 1][j - v[i]] != -1){dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}
-----------------------------------------------------------------------------
// v2.0 滚动数组优化
int main()
{int n = 0, V = 0;cin >> n >> V;vector<int> v(n + 1), w(n + 1);for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}vector<int> dp(V + 1);// Q1for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[V] << endl;// Q2dp.resize(V + 1, 0);for(int i = 1; i <= V; i++){dp[i] = -1;}for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){if(dp[j - v[i]] != -1){dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}}cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}
2.分割等和子集
1.题目链接
- 分割等和子集
2.算法原理详解
- 问题转化:在数组中选择一些数出来,让这些数的和等于
sum / 2--> 01背包 - 思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:从前i个数中**选**,所有的选法中,能否凑成j这个数
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]
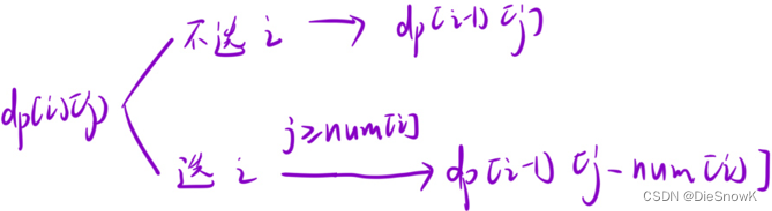
-
初始化:
- 多开一行及一列虚拟结点
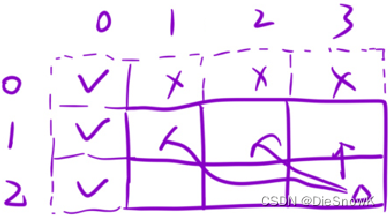
- 多开一行及一列虚拟结点
-
确定填表顺序:从上往下
-
确定返回值:
dp[n][sum / 2]
-
- 滚动数字优化同[模板] 背包
3.代码实现
// v1.0
bool canPartition(vector<int>& nums)
{int n = nums.size(), sum = 0;for(auto& x : nums){sum += x;}if(sum % 2) return false;int aim = sum / 2;vector<vector<bool>> dp(n + 1, vector<bool>(aim + 1));// Initfor(int i = 1; i <= n; i++){dp[i][0] = true;}// DPfor(int i = 1; i <= n; i++){for(int j = 1; j <= aim; j++){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]){dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i - 1]];}}}return dp[n][aim];
}
----------------------------------------------------------------------
// v2.0 滚动数组优化
bool canPartition(vector<int>& nums)
{int n = nums.size(), sum = 0;for(auto& x : nums){sum += x;}if(sum % 2) return false;int aim = sum / 2;vector<bool> dp(aim + 1); dp[0] = true;// DPfor(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] = dp[j] || dp[j - nums[i - 1]];}}return dp[aim];
}