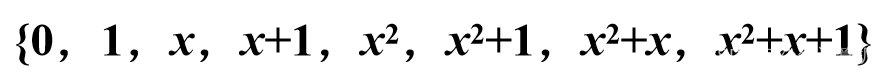题目
交互题,n(n<=1e5)个点的完全图,无向的,初始恰好删了n-2条边
每次询问可以输入一个d:? d
交互器会输出一个当前度>=d的点v,
如果有多个这样的点,输出度最小的,如果还有多个,输出点号最小的
还会输出一个和这个点v当前没有连边的点x,如果x有多个,也输出点号最小的x
如果x不存在,输出x=0
然后交互器会把v这个点和当前连的所有边都删了,
如果没有找到这样的v,交互器输出0 0
最多n次询问后,你需要在「原图」中找到一条哈密顿路径(即一条路径恰访问每个点一次)
按顺序输出哈密顿路径
思路来源
Starsilk Cerulean 稲葉廻
题解
首先要想到问n-2,
问小于n-2肯定是不行的,这样你移除一个点,再也得不到它的信息
但是你只知道它和其中一个点不连接,不知道它另一个不连接的是谁,这样会缺信息
而一直问n-1显然肯定不行,这样会导致剩下的删边越来越多,最后剩下一堆小于n-2的
所以说就问n-2,根据交互器返回的第二维是不是0,
判断当前是n-2还是n-1,n-2时还能知道唯一不连接的是哪个
递归,数学归纳法思想,让剩下来的n个点的图还满足最多去掉n-2条边这个条件
1. 如果问出来的是n-2,显然删掉这个点的子图还满足这个条件,递归子图
2. 如果问出来的是n-1,n-1可以和子图内的点任意连,插入到任何地方,
再选取一个度数最小的点,去掉这两个点后又可以继续递归子图
也就是说,要么一次用到一条删边机会,要么两次用到>=两条删边机会,
使得剩下的x个点图余下的被删掉边的条数<=x-2
严格边数证明可以参考cf,这里可以感性理解一下图的密度(边平均度)

证明完边数之后,就是维护一个双端队列,
1. 不超过2个点,又没有边,直接放即可
2. n-2个点的,只有一条边不能连,判断一下不能和队首连就放到队尾,反之亦然
3. n-1个点的充当媒介,连接当前队尾和当前度最小的点
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
typedef long long ll;
deque<int>q;
int t,n;
P ask(int d){printf("? %d\n",d);fflush(stdout);int x,y;scanf("%d %d",&x,&y);return P(x,y);
}
void sol(int n){if(n<=2){rep(i,1,n){q.push_back(ask(0).fi);}return;}auto [x,y]=ask(n-2);// 要么一次用到一条删边机会,要么两次用到>=两条删边机会,保持图密度不降if(y){sol(n-1);if(q.front()==y)q.push_back(x);else q.push_front(x);}else{auto [y,z]=ask(0);sol(n-2);q.push_back(x);//x都能连q.push_back(y);}
}
void out(){printf("!");while(!q.empty()){int x=q.front();q.pop_front();printf(" %d",x);}printf("\n");fflush(stdout);
}
int main(){sci(t);while(t--){sci(n);q.clear();sol(n);out();}return 0;
}