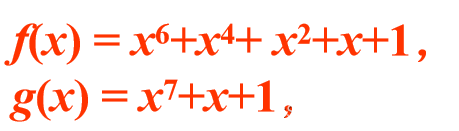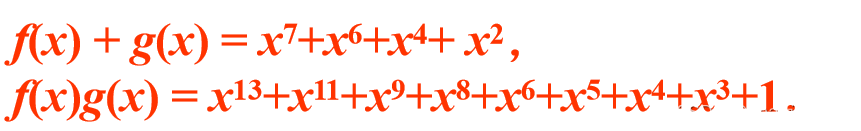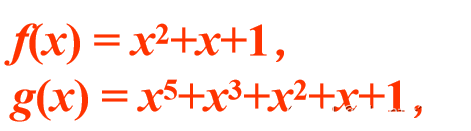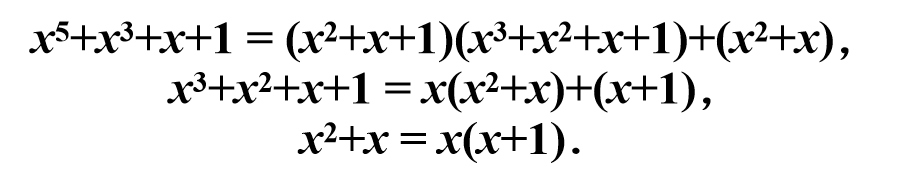5.1 多项式环（掌握）
5.2 多项式剩余类环（理解）
5.3 有限域（熟练）
5.1 多项式环
定义：设F是一个域，称
是F上的一元多项式．
首项：如果an≠0，则称 anx^n 为f(x)的首项
次数：n是多项式f(x)的次数，记为deg(f(x)) = n
首一多项式：如果an = 1，则称f(x)为首一多项式
零次多项式：若f(x) = a0≠0，则约定deg(f(x)) = 0
F上的全体一元多项式的集合用F[x]表示
零多项式：当ai全为0时，f(x)=0，称为零多项式
多项式环运算
对于F[x]中的任意两个多项式
定义F[x]上的加法和乘法分别如下：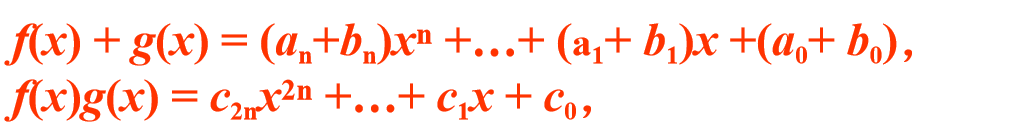
其中
例：域GF(2)上的两个多项式：
则
定理：若F是域，F[x]是具有单位元的整环．
多项式整除
定义：f(x)，g(x)∈F[x]，f(x)≠0．如果存在q(x)∈F[x]，使 g(x) = q(x) f(x)，则称f(x)整除g(x)，记为 f(x)|g(x)， f(x)称为g(x)的因式。如果 f^k(x)|g(x)，但f^(k+1)(x)不能整除g(x)，则称f(x)是g(x)的k重因式．
多项式整除的性质
多项式整除具有下列性质：其中c≠0∈F．
1) f(x)|0；
2) c|f(x) (因为f(x) = c(c^(-1)f(x)))；
3) 如果 f(x)|g(x)，则 cf(x)|g(x)；
4) 如果 f(x)|g(x)，g(x)|h(x)，则 f(x)|h(x)；
5) 如果 f(x)|g(x)，f(x)|h(x)，则对任意u(x)，v(x)∈F[x]，有 f(x)|u(x)g(x)+ v(x)h(x)；
6) 如果 f(x)|g(x)，g(x)|f(x)，则f(x) = cg(x)．
例：Z[x]中有
F[x]的带余除法：对f(x)，g(x)∈F[x]，f(x)≠0，存在q(x)，r(x)∈F[x]，使例：GF(2)[x]上多项式
则
最大公因式
定义：f(x), g(x)∈F[x]为不全为零多项式．设d(x)≠0∈F[x]，如果 d(x)|f(x)，d(x)|g(x)，则称 d(x) 是 f(x),g(x) 的一个公因式。
若d(x)是首一多项式，而且 f(x), g(x) 的任何公因式都整除d(x)，则称d(x)是 f(x), g(x)的最大公因式，记为(f(x)，g(x))。
如果(f(x)，g(x))=1，则称f(x)，g(x)互素。
定理（欧几里德算法）：对于多项式f(x)，g(x)，其中deg(f(x))≤deg(g(x))。反复进行欧几里德除法：
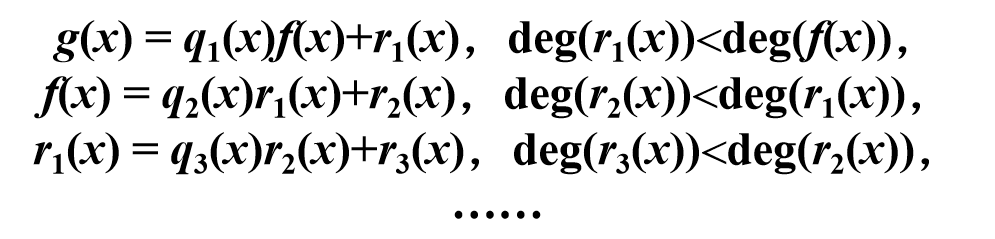
于是
例：求GF(2)[x]上多项式：
解：由欧几里德算法得：
故
定理5-3 对于多项式f(x)，g(x)，其中deg(f(x))≤deg(g(x))，而且h(x) = (f(x)，g(x))．则存在a(x)，b(x)使 a(x)f(x)+b(x)g(x)=h(x)， 其中deg(a(x))≤deg(g(x)), deg(b(x))≤deg(g(x))
特别地，当f(x)，g(x)互素时，存在a(x)，b(x)使 a(x)f(x)+b(x)g(x)=1
多项式的分解
定义：设p(x)∈F[x]为首一多项式，且deg(p(x))≥1，如果p(x)在F[x]内的因式仅有零次多项式及cp(x) (c≠0∈F)，则称p(x)是F[x]内的一个不可约多项式，否则称为可约多项式。
例：Z[x]上多项式
不可约．GF(2)[x]上多项式
GF(2)[x]五次以内的不可约多项式：
定理(分解唯一定理)：F[x]上的多项式
可分解为
，
是两两不同的首一不可约多项式．除
的排列次序外，上述分解是唯一的。
定理：多项式f(x)∈F[x]含有因式 x∈a (a∈F)，当且仅当f(a)=0．
例：分解GF(2)[x]上多项式：
由于f(1)=0，所以f(x)有因式x+1．
运用多项式除法得
通过试探得
故
实际上在GF(2)[x]上有
因此
也可这样分解：
5.2 多项式剩余类环
定义：设f(x)∈F[x]是首一多项式．对于a(x)，b(x)∈F[x]，如果f(x)除a(x)，b(x)得相同的余式，即
则称a(x)和b(x)关于模f(x)同余，记为
由定义可见，a(x)≡b(x) mod f(x)当且仅当 a(x)-b(x)=g(x)f(x)，g(x)∈F[x]，或 f(x)|a(x)-b(x)．
令
是F[x]中关于模f(x)与a(x)同余的全体多项式集合。
与整数情形相似，我们可以把F[x]划分成剩余类，这些剩余类的集合记为F[x] mod f(x)。
例：GF(2)[x]mod
=
定义多项式剩余类的加法和乘法分别如下：
定理：设f(x)∈F[x]是一个首一多项式，且deg(f(x))>0，则F[x]mod f(x)构成具有单位元的交换环，称为多项式剩余类环。多项式剩余类环可能存在零因子，例如GF(2)[x]mod中就有零因子，因为
。
GF(2)[x]mod 存在零因子，是因为是可约多项式．在不可约多项式情形，我们有下面的定理．
定理：如果f(x)是F上的首一不可约多项式，则F[x]mod f(x)构成域．
定理：域F上的多项式F[x]是主理想整环．
5.3 有限域
定义：有限个元素构成的域称为有限域或Galois（伽罗瓦）域．域中元素的个数称为有限域的阶．
我们曾指出，当p是素数时，模p剩余类集合
构成p阶有限域GF(p) 并指出这也是最简单的一种有限域． q阶有限域的所有非零元构成q-1阶乘法交换群．
我们将域中非零元素关于乘法群的阶定义为域中非零元素的阶．
由关于群的讨论我们有，n阶有限群的任意元素a均满足a^n = 1．所 以a^(q-1)=1。
如果把零元也考虑进来，则q阶有限域的所有元素满足 aq=a，或 aq-a = 0
那么q阶有限域可以看成是方程 x^q-x=0的根的集合。
定义：q阶有限域中阶为q-1的元素称为本原域元素，简称本原元。
本原元的意义是很明显的。如果q阶有限域中存在本原元a，则所有非零元构成一个由a生成的q-1阶循环群．那么q阶有限域就可以表示为
定理：有限域中一定含有本原元。实际上，当q>2时，q阶有限域的本原元多于一个。如果a是一个本原元，对于1≤n≤q-1，只要 (n,q-1) = 1， 由群中的结论，则a^n的阶也是q-1，即a^n也是本原元。我们指出，q阶有限域中共有φ(q-1)个本原元（φ是欧拉函数)。
假设a是域中的一个非零元，使
的最小正整数n是a的加法阶．如果不存在这样的n，则加法阶是无限大．
例：GF(7)非零元素的加法阶：
定理：在一个无零因子环R里所有非零元的加法阶都相同。当加法阶有限时，它是一个素数。
定义：域中非零元的加法阶称为域的特征，当加法阶为无限大时，称特征为0。
推论：域的特征或者是0，或者是一个素数．有限域的特征是素数。
例：GF(p)的特征为p，因为
GF(p)的特征等于| GF(p)|．
定理：有限域的阶必为其特征之幂。一般有限域记为GF(p^m)，其中p是域的特征，m是正整数。由于特征总是素数，则有限域的阶总为素数的幂。
定理：如果f(x)是GF(p)上的m次首一不可约多项式，则GF(p)[x] mod f(x)构成pm阶有限域GF(p^m)。
例：GF(2)[x] mod
构成有限域GF(2^3)。
GF(2^3)的8个元素：
为了表示简单，可以去掉上面的横线，但其剩余类的含义没有改变：
