LC121买卖股票的最佳时机（未掌握）

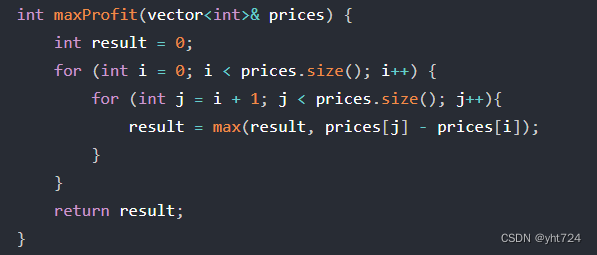
1. 暴力：双层循环寻找最优间距，每一次都确定一个起点，遍历剩余节点当作终点
   
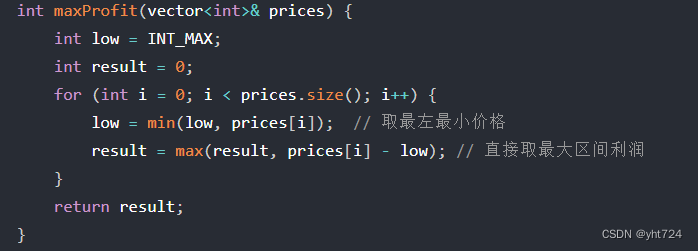
2. 贪心：取最左最小值，不断遍历那么得到的差值最最大值就是最大利润。
   
3. 动态规划
   • dp数组的含义：
     • dp[i][0] 表示第i天持有股票所得最多现金
     • dp[i][1] 表示第i天不持有股票所得最多现金
   • 递归式的推导
     • dp[i][0]=>第i-1天持有和第i天买入的最多现金=>Math.max(dp[i-1][0],-price[i])
     • 因为本金是0，且只能操作一次，所以第i天买入的最多现金为-price[i]
     • dp[i][1]=>第i-1天不持有和第i天卖出的最多现金=>Math.max(dp[i-1][1],dp[i-1][0]+price[i])
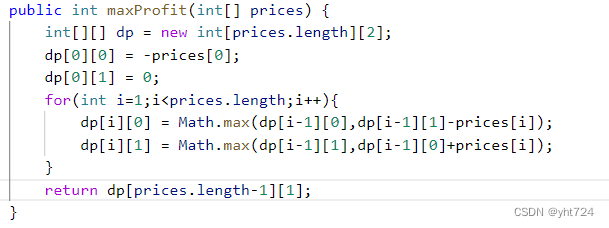
4. 代码
   

LC122买卖股票的最佳时机II

1. 与LC121买卖股票的最佳时机不同的是，LC121只能买入卖出一次，而LC122可以买入卖出多次，因此第i天买入的最多现金为dp[i-1][1]-price[i]
2. 代码
   

LC123买卖股票的最佳时机III(未掌握)

1. LC123与LC122不同的是，LC123只能允许买入两次，而LC122可以买入无数次，因此使用5个状态来记录五种情况
   • 0：无操作，这个状态是用来帮助统计第一次持有股票的情况的
   • 1：第一次持有股票
   • 2：第一次不持有股票
   • 3：第二次持有股票
   • 4：第二次不持有股票
2. 递归公式
   • dp[i][0] = dp[i-1][0]
   • dp[i][1] => 第i-1天第一次就持有股票和第i-1天不持有股票第i天买入 => Math.max(dp[i-1][1], dp[i-1][0]-price[i])
   • dp[i][2] => 第i-1天第一次就不持有股票和第i-1天持有股票第i天卖出 => Math.max(dp[i-1][2], dp[i-1][1]+price[i])
   • dp[i][3] => 第i-1天第二次就持有股票和第i-1天第一次不持有股票第i天买入第二次 => Math.max(dp[i-1][3], dp[i-1][2]+price[i])
   • dp[i][4] => 第i-1天第二次就不持有股票和第i-1天持有第二次股票第i天卖出 => Math.max(dp[i-1][4], dp[i-1][3]+price[i])
3. 初始化：
   • 第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;
   • 第0天做第一次买入的操作，dp[0][1] = -prices[0];
   • 第0天做第一次卖出的操作，可以理解为当天买入，当天卖出，所以dp[0][2] = 0;
   • 第0天第二次买入操作，可以理解为第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），初始化为：dp[0][3] = -prices[0];
   • 同理第二次卖出初始化dp[0][4] = 0;
4. 代码
   

LC188买卖股票的最佳时机IV

1. LC123是买入两次，LC188是买入k次，因此j的值应该设置为2k+1种，代表2k+1种情况
2. 根据规律可知
   • 初始化的时候dp[0][j]，只要j为1、3、5…2*k-1时，值为-price[0]
   • 同理：j两两一组，表示j次买入股票和卖出股票的最多金额
3. 代码