最近我们被客户要求撰写关于MCMC的研究报告，包括一些图形和统计输出。

我们将研究两种对分布进行抽样的方法：拒绝抽样和使用 Metropolis Hastings 算法的马尔可夫链蒙特卡洛方法 (MCMC)。像往常一样，我将提供直观的解释、理论和一些带有代码的示例。

相关视频：马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例

，时长07:25

相关视频

，时长08:47

背景

在我们进入主题之前，让我们将马尔可夫链蒙特卡罗（MCMC）这个术语分解为它的基本组成部分：蒙特卡罗方法和马尔可夫链。

马尔可夫链

 Markov Chain 是“在状态空间上经历从一种状态到另一种状态的转换的随机过程”。

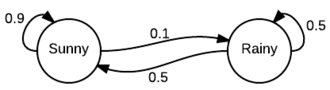
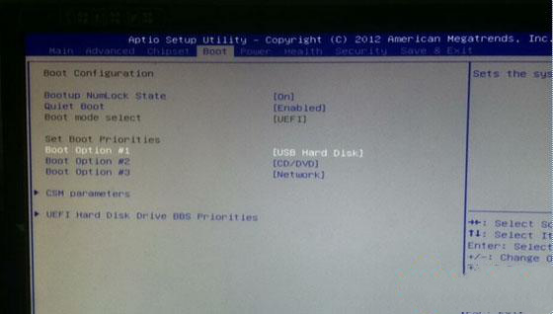
正如你所看到的，它看起来就像一个有限状态机，只是我们用概率注释了状态转换。例如，我们可以查看今天是否晴天，明天晴天的概率为 0.9，下雨的概率为 0.1。同样在雨天开始。应该清楚的是，从给定的状态，所有传出的转换应该总计 1.0，因为它是一个适当的分布。

表示此信息的另一种方法是通过转移矩阵 P：

 

将其表示为矩阵的有趣之处在于，我们可以通过矩阵乘法来模拟马尔可夫链。例如，假设我们从阳光明媚的状态开始，我们可以将其表示为行向量：x(0)=[10]。这隐含地表示我们处于晴天状态的概率为 1，因此处于下雨状态的概率为 0。现在，如果我们执行矩阵乘法，我们可以在一步之后找出处于每个状态的概率： 

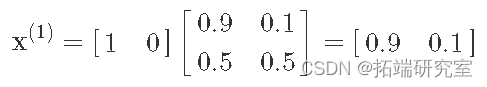
我们可以看到明天有 0.9 的机会晴天（根据我们的简单模型），有 0.1 的机会下雨。实际上，我们可以继续将转换矩阵相乘，以在 k 步之后找到太阳/雨的机会： 

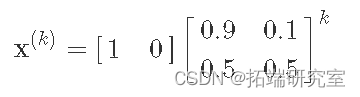
我们可以很容易地计算 x(k) 的各种 k 值，使用 numpy：

import numpy as npPa = nps.ardraasy([[0.9, 0.1], [0.5, 0.5]])
istsdatea = np.arasdray([1, 0])siasdmulatase_markasdov(istaasdte, P, 10)

我们可以在这里看到一个有趣的现象，当我们在状态机中采取更多步骤时，晴天或下雨的概率似乎会收敛。您可能认为这与我们所处的初始状态有关，但实际上并非如此。如果我们将初始状态初始化为随机值，我们将得到相同的结果：

siasmdulasteds_marksov(nap.arsdray([r, 1 - r]), P, 10)
x^(0) = [0.3653 0.6347]
x^(1) = [0.6461 0.3539]
x^(2) = [0.7584 0.2416]
x^(3) = [0.8034 0.1966]
x^(4) = [0.8214 0.1786]
x^(5) = [0.8285 0.1715]
x^(6) = [0.8314 0.1686]
x^(7) = [0.8326 0.1674]
x^(8) = [0.8330 0.1670]
x^(9) = [0.8332 0.1668]

这种稳态分布称为 stationary distribution 通常用 π 表示。可以通过多种方式找到该稳态向量π。最直接的方法是在 nn 接近无穷大时取极限。

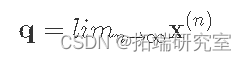
下一种方法就是求解方程。由于根据定义 q是稳态，因此乘以 P 应该返回相同的值： 

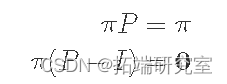
其中 I 是单位矩阵。如果您扩展我们的向量/矩阵符号，您会发现这只是一个方程组以及 π1,π2,...,πn 总和为 1 (即 π 形成概率分布）。在我们的例子中只有两个状态：π1+π2=1。

然而，并不是每个马尔可夫链都有一个平稳的分布，甚至是唯一的 但是，如果我们向马尔可夫链添加两个额外的约束，我们可以保证这些属性：

1. 不可约：我们必须能够最终从任何其他状态到达任何一种状态（即期望步数是有限的）。
2. 非周期性：系统永远不会返回到具有固定周期的相同状态（例如，不会每 5 步确定性地返回开始“晴天”）。

一个重要的定理说，如果马尔可夫链是遍历的，那么它有一个唯一的稳态概率向量 ππ。在 MCMC 的上下文中，我们可以从任何状态跳转到任何其他状态（以一定的有限概率），轻松满足不可约性。

我们将使用的另一个有用的定义是 detailed balance and reversible Markov Chains. 如果存在满足此条件的概率分布 π，则称马尔可夫链是可逆的（也称为详细平衡条件）：

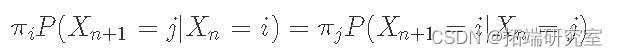
换句话说，从长远来看，你从状态 i 转移到状态 j 的次数比例，与你从状态 j 转移到状态 i 的次数比例相同。事实上，如果马尔可夫链是可逆的，那么我们就知道它具有平稳分布（这就是我们使用相同符号 π 的原因）。

马尔可夫链蒙特卡罗方法

马尔可夫链蒙特卡罗 (MCMC) 方法只是一类使用马尔可夫链从特定概率分布（蒙特卡罗部分）中采样的算法。他们通过创建一个马尔可夫链来工作，其中限制分布（或平稳分布）只是我们想要采样的分布。

这是一张可能有助于描述该过程的图片. 想象一下，我们正在尝试制作一个 MCMC 来尝试使用 PDF f(x)对任意一维分布进行采样。在这种情况下，我们的状态将是沿 x 轴的点，而我们的转换概率将是从一种状态到另一种状态的机会。这是情况的简化图：

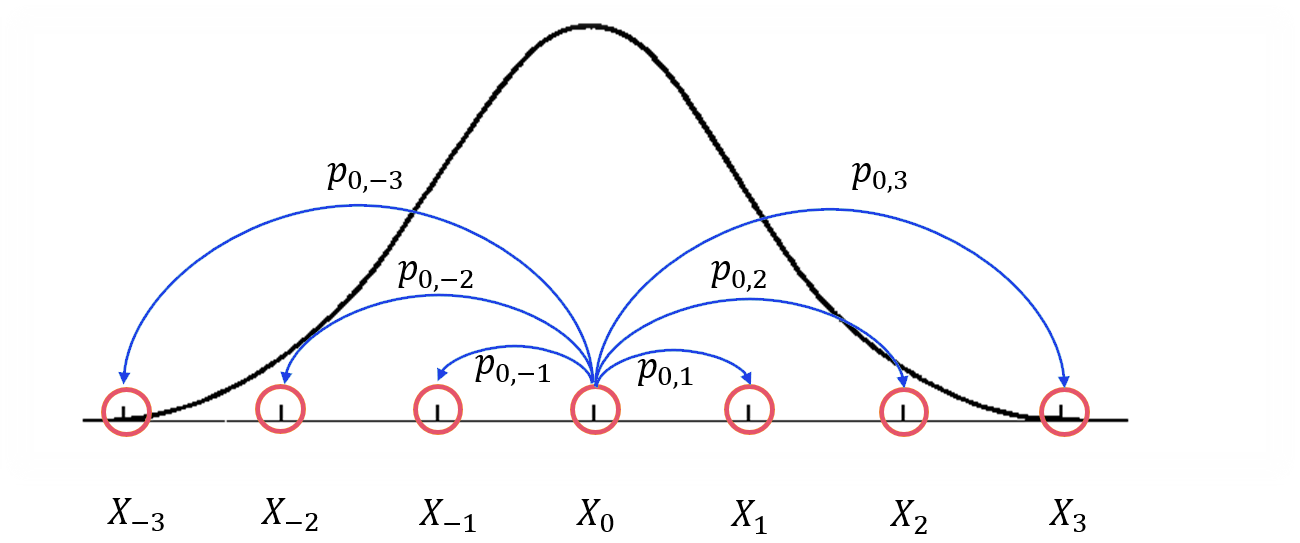
该图显示了我们试图用粗黑线逼近的密度函数，以及使用从橙色状态过渡的蓝线的马尔可夫链的一部分的可视化。特别是，对于 i=-3,-2,-1,1,2,3，只是从状态 X0 到 Xi 的转换。但是，x 轴线上的每个点实际上都是这个马尔可夫链中的一个势态。请注意，这意味着我们有一个无限的状态空间，因此我们不能再将转换很好地表示为矩阵。MCMC 方法的真正“诀窍”是我们想要设计状态（或 x 轴上的点）之间的转换概率，以便我们将大部分时间花在 f(x) 很大的区域中，并且在它较小的区域中的时间相对较少（即与我们的密度函数成精确比例）。

就我们的人物而言，我们希望将大部分时间花在中心周围，而较少时间花在外面。事实上，如果我们模拟我们的马尔可夫链足够长的时间，状态的限制分布应该近似于我们试图采样的 PDF。因此，使用 MCMC 方法进行采样的基本算法为：

1. 从任意点 x 开始。
2. 以一定的转移概率跳转到点 x'（这可能意味着保持相同的状态）。
3. 转到第 2 步，直到我们转换了 T 时间。
4. 记录当前状态 x′，进行步骤 2。

现在，我们在每个点 x 轴上花费的比例次数应该是我们试图模拟的 PDF 的近似值，即如果我们绘制 x 值的直方图，我们应该得到相同的形状。

拒绝抽样

现在，在我们进入 MCMC 方法的具体算法之前，我想介绍另一种对概率分布进行采样的方法，我们稍后将使用它，称为 rejection sampling. 主要思想是，如果我们试图从分布 f(x) 中采样，我们将使用另一个工具分布 g(x) 来帮助从 f(x) 中采样。唯一的限制是对于某些 M>1，f(x)<Mg(x)。它的主要用途是当 f(x) 的形式难以直接采样时（但仍然可以在任何点 xx 对其进行评估）。

以下是算法的细分：

1. 从 g(x) 中采样 x。
2. 从 U(0,Mg(x)) 中采样 y（均匀分布）。
3. 如果 y<f(x)，则接受 x 作为 f(x) 的样本，否则转到步骤 1。

另一种看待它的方法是我们采样点 x0 的概率。这与从 g 中采样 x0 的概率乘以我们接受的次数的比例成正比，它简单地由 f(x0) 和 Mg(x0) 之间的比率给出：

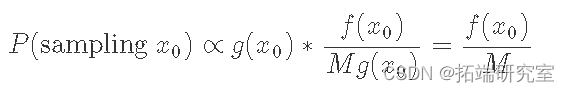
等式告诉我们对任意点进行采样的概率与 f(x0) 成正比。在对许多点进行采样并找到我们看到 x0 的次数比例之后，常数 M 被归一化，我们得到了 PDF f(x) 的正确结果。

让我们通过一个例子更直观地看一下它。我们要从中采样的目标分布 f(x) 是 double gamma 分布，基本上是一个双边伽马分布。我们将使用正态分布 g(x) 作为我们的包络分布。下面的代码向我们展示了如何找到缩放常数 M，并为我们描绘了拒绝抽样在概念上是如何工作的。

# 目标 = 双伽马分布
dsg = stats.dgamma(a=1)# 生成PDF的样本
x = np.linspace# 绘图
ax = df.plot(style=['--', '-']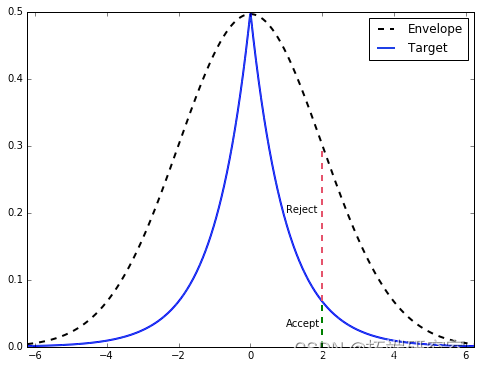

 

从图中，一旦我们找到 g(x)的样本（在这种情况下 x=2），我们从范围等于 Mg(x) 高度的均匀分布中绘制. 如果它在目标 PDF 的高度内，我们接受它（绿色），否则拒绝（拒绝）。

实施拒绝抽样

下面的代码为我们的目标双伽马分布实现拒绝采样。它绘制标准化直方图并将其与我们应该得到的理论 PDF 匹配。

# 从拒绝采样算法生成样本
sdampales = [rejeasdctioan_samplaing for x in range(10000)]# 绘制直方图与目标 PDF
df['Target'].plot

 

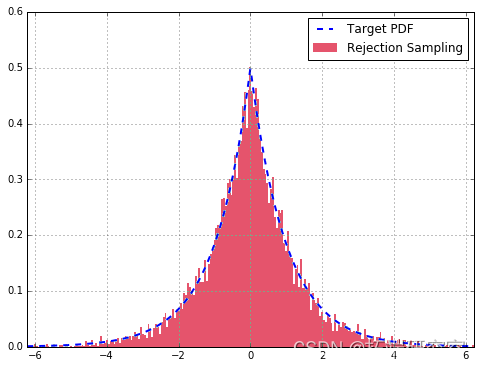
总的来说，我们的拒绝采样器非常适合。与理论分布相比，抽取更多样本会改善拟合。

拒绝抽样的很大一部分是它很容易实现（在 Python 中只需几行代码），但有一个主要缺点：它很慢。

Metropolis-Hastings 算法

这 Metropolis-Hastings Algorithm (MH) 是一种 MCMC 技术，它从难以直接采样的概率分布中抽取样本。与拒绝抽样相比，对 MH 的限制实际上更加宽松：对于给定的概率密度函数 p(x)，我们只要求我们有一个  与 p成正比的函数 f(x)f(x) (x)p(x)！这在对后验分布进行采样时非常有用。

Metropolis-Hastings 算法的推导

为了推导出 Metropolis-Hastings 算法，我们首先从最终目标开始：创建一个马尔可夫链，其中稳态分布等于我们的目标分布 p(x)。就马尔可夫链而言，我们已经知道状态空间将是什么：概率分布的支持，即 x 值。因此（假设马尔可夫链的构造正确）我们最终得到的稳态分布将只是 p(x)。剩下的是确定这些 x 值之间的转换概率，以便我们可以实现这种稳态行为。

马尔可夫链的详细平衡条件，这里用另一种方式写成：

这里 p(x)是我们的目标分布，P(x→x′) 是从点 x到点 x′ 的转移概率。所以我们的目标是确定P(x→x′)的形式。既然我们要构建马尔可夫链，让我们从使用等式 5 作为该构建的基础开始。请记住，详细的平衡条件保证我们的马尔可夫链将具有平稳分布（它存在）。此外，如果我们也包括遍历性（不以固定间隔重复状态，并且每个状态最终都能够达到任何其他状态），我们将建立一个具有唯一平稳分布 p(x)的马尔可夫链.

我们可以将方程重新排列为：

 

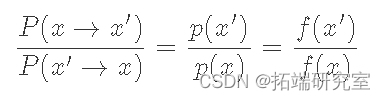
这里我们使用 f(x)来表示一个  与 p(x)成正比的函数。这是为了强调我们并不明确需要 p(x)，只是需要与它成比例的东西，这样比率才能达到相同的效果。现在这里的“技巧”是我们将把 P(x→x′)分解为两个独立的步骤：一个提议分布 g(x→x′) 和接受分布 A(x→x′)（类似于拒绝抽样的工作原理）。由于它们是独立的，我们的转移概率只是两者的乘积： 

 

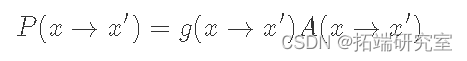
此时，我们必须弄清楚 g(x)和 A(x) 的合适选择是什么。由于 g(x) 是“建议分布”，它决定了我们可能采样的下一个点。因此，重要的是它具有与我们的目标分布 p(x)（遍历性条件）相同的支持。这里的一个典型选择是以当前状态为中心的正态分布。现在给定一个固定的提议分布 g(x)，我们希望找到一个匹配的 A(x)。

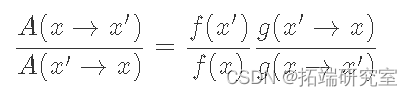
虽然不明显，但满足公式 的 A(x) 的典型选择是： 

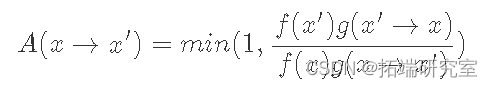
我们可以通过考虑 f(x′)g(x′→x)小于等于 1 和大于 1 的情况。当小于等于 1 时，它的倒数大于 1，因此 LHS 的分母，A(x′→ x), 等式 8 为 1，而分子等于 RHS。或者，当f(x′)g(x′→x)是大于 1 LHS 的分子是 1，而分母正好是 RHS 的倒数，导致 LHS 等于 RHS。

这样，我们已经证明，我们创建的马尔可夫链的稳定状态将等于我们的目标分布 (p(x))，因为详细的平衡条件通过构造得到满足。所以整体算法将是（与上面的 MCMC 算法非常匹配）：

1. 通过选择一个随机 x 来初始化初始状态。
2. 根据g(x→x′)找到新的x′。
3. 根据 A(x→x′) 以均匀概率接受 x′。如果接受到 x' 的转换，否则保持状态 x。
4. 进行第 2 步，T 次。
5. 将状态 x 保存为样本，转至步骤 2 对另一个点进行采样。

预烧和相关样本

在我们继续实现之前，我们需要讨论关于 MCMC 方法的两个非常重要的话题。第一个主题与我们选择的初始状态有关。由于我们随机选择 xx 的值，它很可能位于 p(x) 非常小的区域（想想我们的双伽马分布的尾部）。如果从这里开始，它可能会花费不成比例的时间来遍历低密度的 x 值，从而错误地给我们一种感觉，即这些 x 值应该比它们更频繁地出现。所以解决这个问题的方法是“预烧”采样器通过生成一堆样本并将它们扔掉。样本的数量将取决于我们试图模拟的分布的细节。

我们上面提到的第二个问题是两个相邻样本之间的相关性。由于根据我们的转换函数 P(x→x′)的定义，绘制 x′ 取决于当前状态 x。因此，我们失去了样本的一项重要属性：独立性。为了纠正这一点，我们抽取 Tth 个样本，并且只记录最后抽取的样本。假设 T 足够大，样本应该是相对独立的。与预烧一样，T 的值取决于目标和提议分布。

实现 Metropolis-Hastings 算法

让我们使用上面的双伽马分布示例。让我们将我们的提议分布定义为以 x 为中心、标准差为 2、N(x, 2) 的正态分布（记住 x 是当前状态）：

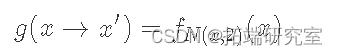
给定 f(x) 与我们的基础分布 p(x) 成比例，我们的接受分布如下所示： 

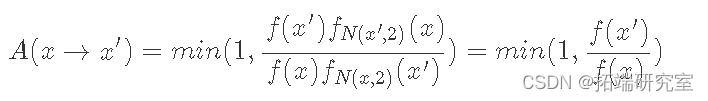
由于正态分布是对称的，因此正态分布的 PDF 在其各自点进行评估时会相互抵消。现在让我们看一些代码：

# 模拟与双伽马分布成比例的 f(x)
f = ambd x: g.df(x* mat.i采样器 = mhspler()＃ 样本
sames = [nex(saper) for x in range(10000)]# 绘制直方图与目标 PDF
df['Target'].plot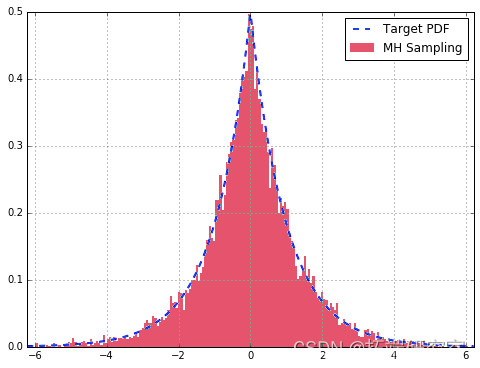

 

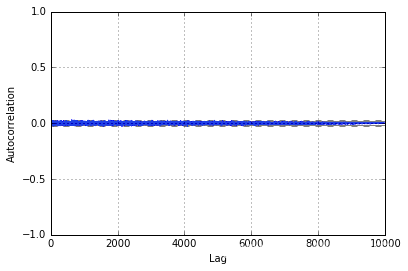
来自我们的 MH 采样器的样本很好地近似于我们的双伽马分布。此外，查看自相关图，我们可以看到它在整个样本中非常小，表明它们是相对独立的。如果我们没有为 T 选择一个好的值或没有预烧期，我们可能会在图中看到较大的值。

结论

我希望你喜欢这篇关于使用拒绝抽样和使用 Metropolis-Hastings 算法进行 MCMC 抽样的简短文章。

---