期望最大化 (Expectation Maximization) 算法最初是由 Ceppellini[2] 等人 1950 年在讨论基因频率的估计的时候提出的。后来又被 Hartley[3] 和Baum[4] 等人发展的更加广泛。目前引用的较多的是 1977 年 Dempster[5]等人的工作。它主要用于从不完整的数据中计算最大似然估计。后来经过其他学者的发展，这个算法也被用于聚类等应用。

因此如果大家理解了K-means聚类，那么这个算法就容易理解了，这里我们先一起来回归一下K-means的聚类思想，其实他的聚类思想很简单，我们来看一下算法过程：

k-means的k就是最终聚集的簇数，这个要你事先自己指定。k-means在常见的机器学习算法中算是相当简单的，基本过程如下：

首先任取k个样本点作为k个簇的初始中心；
对每一个样本点，计算它们与k个中心的距离，把它归入距离最小的中心所在的簇；
等到所有的样本点归类完毕，重新计算k个簇的中心；
重复以上过程直至样本点归入的簇不再变动。

通过上面大家可以看到，为了找到合适的聚类中心点，k-means刚开始给的初始中心是任意的，然后不断的更新迭代后按照上面算法步骤不停的更改k个中心的位置，直到他们都几乎不再变化位置，也就是说当k个位置几乎不再变化时基本上就说明了到达了真实的数据中心了。这里有一个思想就是我刚开始不知道数据的最佳K个中心点，但是我可以通过数据不停的迭代，进而达到理想的中心点，而这个思想也是EM算法的核心思想。
下面先通过一个简单的例子引入EM算法的核心思想，然后在使用数学进行证明这样做的合理性。

EM

考虑一个投掷硬币的实验：现在我们有两枚硬币 A 和 B，这两枚硬币和普通的硬币不一样，他们投掷出正面的概率和投掷出反面的概率不一定相同。我们将 A 和 B 投掷出正面的概率分别记为 $\theta _A$ 和 $\theta _B$ 。我们现在独立地做 5 次试验：随机的从这两枚硬币中抽取 1 枚，投掷 10 次，统计出现正面的次数。那么我们就得到了如表格1的实验结果。

试验代号

投掷的硬币

出现正面的次数

在这个实验中，我们记录两组随机变量：

$X = (X_1,X_2,X_3,X_4,X_5)$

$Z = (Z_1,Z_2,Z_3,Z_4,Z_5)$

其中 $X_i\in \left \{ 1,2,3,4,5,6,7,8,9,10 \right \}$ ，代表试验 $i$ 中出现的正面的次数， $Z_i\in \left \{ A,B \right \}$ 代表这次试验投掷的是硬币A还是B。

我们的目标是通过这个实验来估计 $\theta =(\theta _A,\theta _B)$ 的数值。这个实验中的参数估计就是有完整数据的参数估计，这个是因为我们不仅仅知道每次试验中投掷出正面的次数，我们还知道每次试验中投掷的是硬币 A 还是 B。
一个很简单也很直接的估计 θ 的方法如公式(1)所示。

实际上这样的估计就是统计上的极大似然估计 (maximum likelihood estimation) 的结果。用 $P(X,Z|\theta )$ 来表示 $X,Z$ 的联合概率分布（其中带有参数 θ），那么对于上面的实验，我们可以计算出他们出现我们观察到的结果即 $x^0 = (5,9,8,4,7),z^0 = (B,A,A,B,A)$ 的概率。函数 $P(X=x^{(0)},Z = z^{0}|\theta )$ 就叫做 θ 的似然函数。我们将它对 θ 求偏导并令偏导数为 0，就可以得到如(1) 的结果。

对其求偏导，这里只对 $\theta _A$ 求偏导， $\theta _B$ 也是一样的求，这里我们把系数统一使用C来表示了，关于 $\theta _B$ 的式子使用 $f(\theta _B)$ 进行代替，然后整理一下上式得：

$P(X=x^0,Z = z^0|\theta ) = Cf(\theta _B)\theta _A^{24}(1-\theta _A)^6$

对其求偏导，并令其为0的：

$\frac{\partial P(X=x^0,Z = z^0|\theta )}{\partial \theta _A} = Cf(\theta _B)[24\theta _A^{23}(1-\theta _A)^6-6\theta ^{24}(1-\theta _A)^5]=0$

此时化简解得 $\theta _A$ 如下：

$24(1-\theta _A) - 6\theta _A = 0$

$30\theta _A = 24$

$\theta _A = 0.8$

同理可求 $\theta _B =0.45$

由此可见上面利用均值和这里使用最大释然函数的结果是一样的，因此这里的（1）式称为极大释然估计。这里大家应该明白了吧。下面我们把难度加大：

我们将这个问题稍微改变一下，我们将我们所观察到的结果修改一下：我们现在只知道每次试验有几次投掷出正面，但是不知道每次试验投掷的是哪个硬币，也就是说我们只知道表1中第一列和第三列。这个时候我们就称 $Z$ 为隐藏变量 (Hidden Variable)， $X$ 称为观察变量 (Observed Variable)。这个时候再来估计参数 $\theta _A$ 和 $\theta _B$ ，就没有那么多数据可供使用了，这个时候的估计叫做不完整数据的参数估计（这里X就可认为是HMM中的可见变量了，Z就是隐藏的状态变量了）。
如果我们这个时候有某种方法（比如，正确的猜到每次投掷硬币是 A还是 B），这样的话我们就可以将这个不完整的数据估计变为完整数据估计。
当然我们如果没有方法来获得更多的数据的话，那么下面提供了一种在这种不完整数据的情况下来估计参数 θ 的方法。我们用迭代的方式来进行：

(1) 我们先赋给 θ 一个初始值，这个值不管是经验也好猜的也好，反正我们给它一个初始值。在实际使用中往往这个初始值是有其他算法的结果给出的，当然随机给他分配一个符合定义域的值也可以。这里我们就给定 $\theta _A$ = 0.7, $\theta _B$ = 0.4
(2) 然后我们根据这个来判断或者猜测每次投掷更像是哪枚硬币投掷的结果。比如对于试验 1，如果投掷的是 A，那么出现 5 个正面的概率为 $C_{10}^5\times 0.7^5\times (1-0.7^5)\approx 0.1029$ ；如果投掷的是B，出现5个正面的概率为 $C_{10}^5\times 0.4^5\times (1-0.4)^5\approx 0.2007$ ；基于试验1的试验结果，可以判断这个试验投掷的是硬币 A 的概率为 0.1029/(0.1029+0.2007)=0.3389，是 B 的概率为 0.2007/(0.1029+0.2007)= 0.6611。因此这个结果更可能是投掷 B 出现的结果。
(3) 假设上一步猜测的结果为 B,A,A,B,A，那么根据这个猜测，可以像完整数据的参数估计一样 (公式2) 重新计算 θ 的值。

这样一次一次的迭代 2-3 步骤直到收敛，我们就得到了 θ 的估计。这里大家应该能感受到这和K-means很像对吧，你可能有疑问，这个方法靠谱么？事实证明，它确实是靠谱的。下面我们就从数学角度来说明他的合理性。

数学证明

首先来明确一下我们的目标：我们的目标是在观察变量 X 和给定观察样本 $x_1,x_2,...,x_n$ 的情况下，极大化对数似然函数

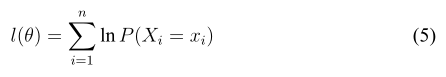
这个函数大家应该都能看懂吧，看不懂的请返回看我的上一篇博客。

其中只包含观察变量的概率密度函数（其实是求边缘密度，即对另一个变量进行求和就可以了得到边缘密度了）：

其中 Z 为隐藏随机变量, $\left \{ Z_j \right \}$ 是 Z 的所有可能的取值。那么把（6）式代入（5）式：

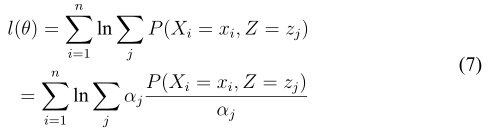
这里我们引入了一组参数（不要怕多，我们后面会处理掉它的）α，它满足∀可能的j, $\alpha _j$ ∈ (0,1]和
$\sum _j\alpha _j=1$ 到这里，先介绍一个凸函数的性质，或者叫做凸函数的定义。f(x) 为凸函数， $\forall i = 1,2,3,..,n,\lambda _i\in [0,1],\sum_{i=1}^{n}\lambda _i = 1$ ,对 f(x) 定义域中的任意 n 个 $x_1,x_2,...,x_n$ 有 :

$f(\sum_{i=1}^{n}\lambda _ix_i)\leq \sum_{i=1}^{n}\lambda _if(x_i)$ $\left ( 8 \right )$

上式称为Jensen不等式

对于严格凸函数，上面的等号只有在 $x_1= x_2=...=x_n$ 的时候成立。关于凸函数的其他性质不再赘述。对数函数是一个严格凸函数。因而我们可以有下面这个结果：

上式是 $\left ( 7 \right )$ 式根据 $\left ( 8 \right )$ 式得到的，只是不同的是ln是凹函数，但是同样适用Jensen不等式，只是不等号方向不一样罢了。

现在我们根据等号成立的条件来确定 $\alpha _j$ 即

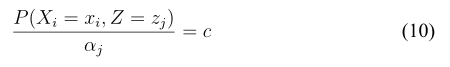
这里需仔细推一下，我们知道 $\left ( 9 \right )$ 的成立条件是 $x_1= x_2=...=x_n$ ，那么联合概率密度 $P(X_i,Z_j)$ 是不变的，等于一个常数，和j无关，和j无关的意思是当j确定时，无论i等于几上式都是一个常数，大家可以这样理解，因此可以写成 $\left ( 10 \right )$ 式，对上式的j求和同时把 $\alpha _j$ 乘到右边：

$\sum_{j}P(X_i=x_i,Z=z_j) = \sum _j\alpha _j*c = c$

我们仔细看看等式的左边，他是对j求和，而且P是联合概率密度，对某一个维度求和不就是求边缘密度吗？所以上式可以写为如下：

$\sum_{j}P(X_i=x_i,Z=z_j) = P(X_i=x_i)=\sum _j\alpha _j*c = c$

也就是说：

$P(X_i=x_i) = c$

此时把上式代入（10）式，可得（11）式

其中 c 是一个与 j 无关的常数。因为 $\sum _j\alpha _j=1$ 稍作变换就可以得到

上式是什么意思呢？大家还记得条件概率的定义吗？

$P(B|A) = \frac{P(AB)}{P(A)}$

因此（11）式就是条件概率的表达式即为 $P(Z=z_j|X=x_i) = \frac{P(X_i=x_i,Z=z_j)}{P(X=x_i)}$ .，这个式子代表什么意思呢？其实就是在我们知道了扔的硬币为正的情况下这个硬币为A或者为B的概率，就是再求隐藏的条件概率。

现在来解释一下我们得到了什么。 $\alpha _j$ 就是 $Z=z_j$ 在 $X=x_i$ 下的条件概率或者后验概率。求 α 就是求隐藏随机变量 Z 的条件分布。总结一下目前得到的公式就是

好，得到上式以后，我们如何求 $\theta$ 呢，这里需要和大家说明的是，这里的 $\theta$ 在上式没体现处理，他是包含在P和 $\alpha$ 中的，这里大家需要理解，那我们如何求解参数 $\theta$ 使的 $l(\theta )$ 达到最大呢？这里我们需要明确上式是很复杂的，直接求导不好求，因此需要想办法进行间接求极大值，怎么求呢？这里给出一个简单的例子：

$l(\theta )=d(\theta )q\left ( \theta \right )$

假设有一个待求极值的函数 $l(\theta )$ ，如上式，其中 $d(\theta )$ 很复杂无法求导，而 $q(\theta )$ 相对简单一点，那么针对这样的函数我们如何求极值呢？这里提供一种迭代的方法，首先我给 $d(\theta )$ 任意赋值一个 $\theta _0$ 的值，此时 $d(\theta _0)$ 就是一个常数了，那么上式就可以写成 $l(\theta )=d(\theta_0 )q\left ( \theta \right )$ ，此时在对 $l(\theta )$ 求导得到 $\theta _1$ ,再把 $\theta _1$ 代入 $d(\theta )$ ，在类似的计算，直到 $\theta$ 不再发生变化此时的 $\theta$ 就是所求的值，过程如下：