题目
中等
相关标签
相关企业
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:
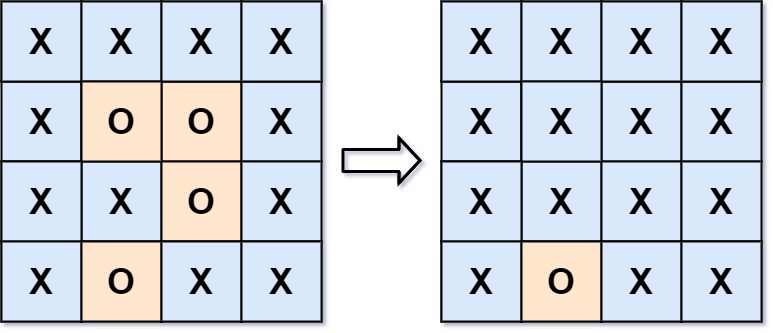
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] 解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的'O'都不会被填充为'X'。 任何不在边界上,或不与边界上的'O'相连的'O'最终都会被填充为'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]] 输出:[["X"]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
通过次数 285.7K
提交次数 614.4K
通过率 46.5%
方法一:并查集
利用并查集,将相邻的相同字母视为一个连通集。边界上的'O'视为同一个集,易得,不与边界上的'O'相邻的'O'即为被围绕的区域。
下面是某位大佬的java代码
class UnionFind {int[] parents;public UnionFind(int totalNodes) {parents = new int[totalNodes];for (int i = 0; i < totalNodes; i++) {parents[i] = i;}}// 合并连通区域是通过find来操作的, 即看这两个节点是不是在一个连通区域内.void union(int node1, int node2) {int root1 = find(node1);int root2 = find(node2);if (root1 != root2) {parents[root2] = root1;}}int find(int node) {while (parents[node] != node) {// 当前节点的父节点 指向父节点的父节点.// 保证一个连通区域最终的parents只有一个.parents[node] = parents[parents[node]];node = parents[node];}return node;}boolean isConnected(int node1, int node2) {return find(node1) == find(node2);}
}
class Solution {int rows;int cols;public void solve(char[][] board) {if (board == null || board.length == 0)return;rows = board.length;cols = board[0].length;// 用一个虚拟节点, 边界上的O 的父节点都是这个虚拟节点UnionFind uf = new UnionFind(rows * cols + 1);int dummyNode = rows * cols;for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (board[i][j] == 'O') {// 遇到O进行并查集操作合并if (i == 0 || i == rows - 1 || j == 0 || j == cols - 1) {// 边界上的O,把它和dummyNode 合并成一个连通区域.uf.union(node(i, j), dummyNode);} else {// 和上下左右合并成一个连通区域.if (i > 0 && board[i - 1][j] == 'O')uf.union(node(i, j), node(i - 1, j));if (i < rows - 1 && board[i + 1][j] == 'O')uf.union(node(i, j), node(i + 1, j));if (j > 0 && board[i][j - 1] == 'O')uf.union(node(i, j), node(i, j - 1));if (j < cols - 1 && board[i][j + 1] == 'O')uf.union(node(i, j), node(i, j + 1));}}}}for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (uf.isConnected(node(i, j), dummyNode)) {// 和dummyNode 在一个连通区域的,那么就是O;board[i][j] = 'O';} else {board[i][j] = 'X';}}}}int node(int i, int j) {return i * cols + j;}}
方法二:深度优先搜索
前面提到,不与边界的'O'连通的'O'即为被包围的区域。所以我们可以以四条边上的'O'为起点搜索,将与边界'O'连通的'O'做个标记,随后有标记的'O'就改回'O',没有标记的'O'就变成'X'。
class Solution {
public:void dfs(vector<vector<char>>& board,int x,int y,int n,int m){if(x<0||x>=n||y<0||y>=m||board[x][y]!='O'){return;}board[x][y]='Y';dfs(board,x+1,y,n,m);dfs(board,x,y-1,n,m);dfs(board,x-1,y,n,m);dfs(board,x,y+1,n,m);}void solve(vector<vector<char>>& board) {int n=board.size();if(n==1) return;int m=board[0].size();if(m==1) return;for(int i=0;i<n;i++){dfs(board,i,0,n,m);dfs(board,i,m-1,n,m);}for(int j=1;j<m-1;j++){dfs(board,0,j,n,m);dfs(board,n-1,j,n,m);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(board[i][j]=='Y')board[i][j]='O';else if(board[i][j]=='O')board[i][j]='X';}}}
};