专栏引入
哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我想让大家知道的是:数据结构非常有趣,很多算法是智慧的结晶,我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏,在这里我将把数据结构内容以有趣易懂的方式展现给大家。
1.二叉树的链式存储结构
前面我们说过顺序存储结构一般只适用于完全二叉树,既然顺序存储适应性不强,我们既要考虑链式存储结构了。二叉树每个节点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法 ,我们称这样的链表为二叉链表。节点结构图如下所示:

其中,data是数据域,leftchild和rightchild都是指针域,分别存放指向左孩子和右孩子的指针,下面是二叉链表的节点结构定义代码:
typedef struct BinaryTreeNode
{TDataType data;struct TreeNode* leftchild;struct TreeNode* rightchild;
}BTNode;结构示意图如下:
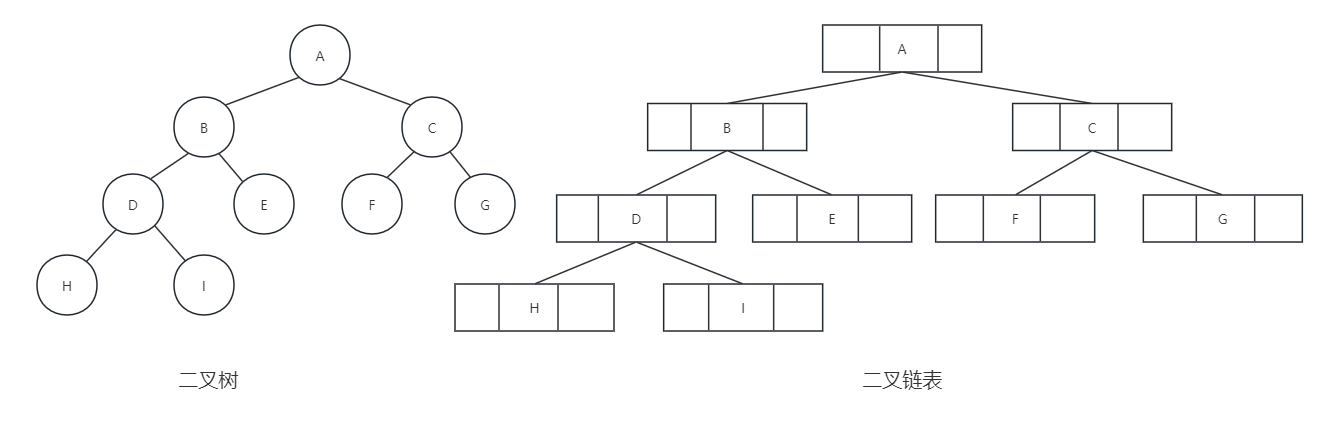
就如同我们在树的存储结构中讨论的一样,如果有需要,还可以增加一个指针指向其双亲的指针域,那样就称之为三叉链表,后续在红黑树时会提到,这里就不细讲了。
2.二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中的所有节点,使得每一个节点被访问一次且仅被访问一次。这里有两个关键词:访问和次序。访问其实是根据实际需要来确定具体做什么,比如:对某个节点进行相关计算、输出打印等。二叉树的遍历次序不同于线性结构,最多也就是从头到尾、循环、双向等简单的遍历方式。树的节点之间不存在唯一的前驱和后继关系,在访问一个节点后,下一个访问的节点面临着不同的选择。就像我们高考填报志愿要面临着去哪个城市、哪所大学、具体专业等选择,由于选择的方式不同,遍历的次序就完全不同了。
二叉树的遍历方式可以有很多种,如果我们限制了从左到右的习惯方式,那么主要就分为四种:前序遍历、中序遍历、后序遍历、层序遍历。
2.1前序遍历
二叉树的前序遍历规则是:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树。即按照“根节点-左子树-右子树”的顺序遍历二叉树。像下面这张图中的二叉树,遍历顺序是ABDECFG:

二叉树的定义是用递归的方式,所以,实现遍历也可以采用递归,而且极其简洁明了,我们先来看看二叉树的前序遍历,具体代码如下:
void PreOrderTraverse(BiTree T)
{if(T==null)return;printf("%c",T->data);PreOrderTraverse(T->lchild);preOrderTraverse(T->rchild);
}假设我们有如下图这样的一棵二叉树T,这棵树已经用二叉链表结构存储在内存当中:
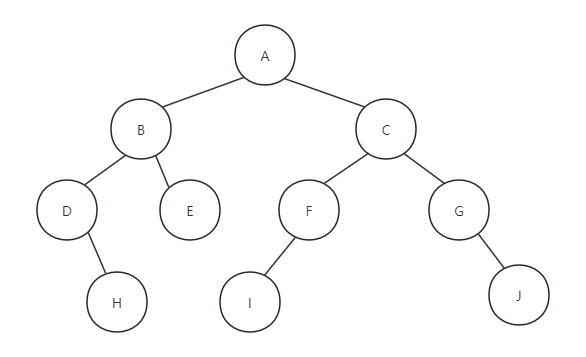
当我们调用PreOrderTraverse(T)函数时,我们来看看程序是怎么运行的:
(1)当调用PreOrderTraverse(T)时,根节点不为NULL,所以执行printf,打印字母A,就像下面这样:
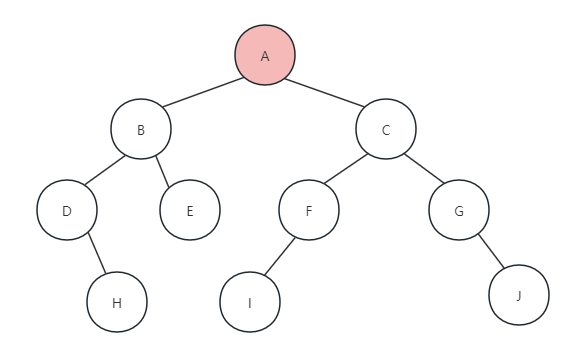
(2)接着我们调用PreOrderTraverse(T->lchild)函数,访问根节点A的左孩子,不为NULL,执行printf打印字母B,如下图所示:

(3)此时再次递归调用PreOrderTraverse(T->lchild)函数,来访问B节点的左孩子,执行printf函数打印字母D,如下图所示:
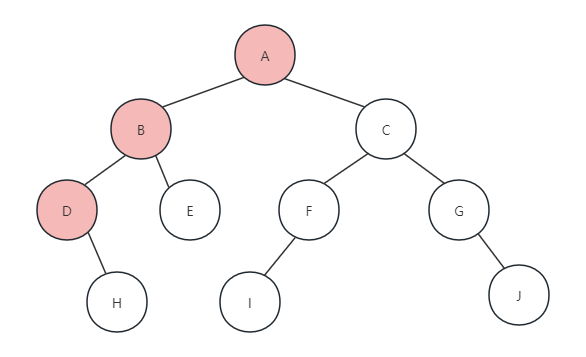
(4)再次递归调用PreOrderTraverse(T->rchild),访问D节点的左孩子,此时因为D节点没有左孩子,所以T=NULL,返回此函数,此时递归调用PreOrderTraverse(T->rchild),访问D节点的右孩子,执行printf打印H,如下图所示:
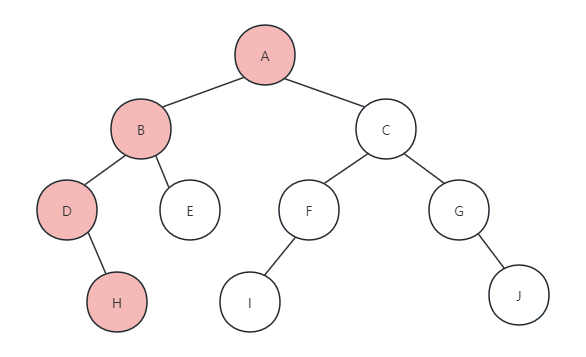
(5) 再次递归调用PreOrderTraverse(T->lchild),访问H节点的左孩子,H节点没有左孩子,返回,调用PreOrderTraverse(T->rchild),访问H节点的右孩子,也是NULL,返回。于是,此函数执行完毕,返回到上一级递归的函数(即打印D节点的函数),也执行完毕,返回打印D节点时的函数,调用PreOrderTraverse(T->rchild),找到E节点,打印字母E,如下图所示:
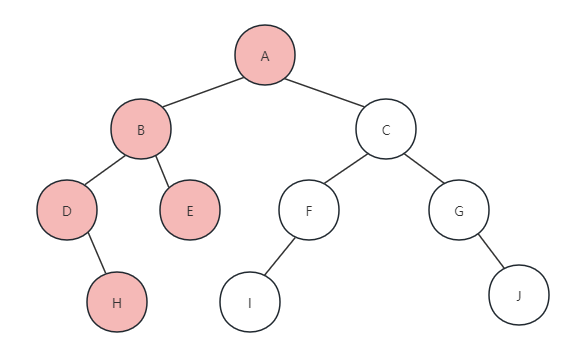
(6)由于节点E没有左右孩子,返回打印B节点的递归函数,递归执行完毕,返回到最初的PreOrderTraverse,调用PreOrderTraverse(T->rchild),访问A节点的右孩子,如图所示:
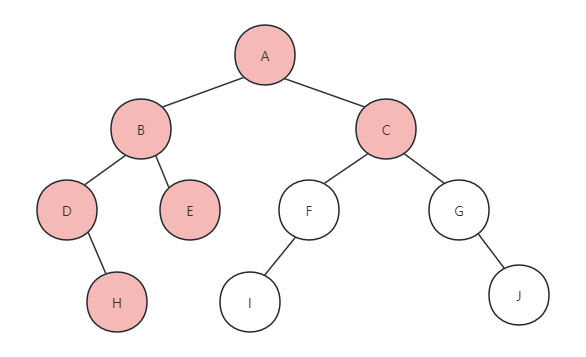
(7)之后类似前面的递归调用,一依次打印F、I、G、J,这里步骤就省略喽。
综上所述,前序遍历这棵二叉树的节点的顺序是ABDHECFIGJ。
2.2中序遍历
规则是若树为空,则空操作返回,否则从根节点开始(注意不是先访问根节点),中序遍历是遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树,即按照“左子树-根节点-右子树”的顺序遍历二叉树。如下图所示的二叉树遍历的顺序为DBEAFCG:
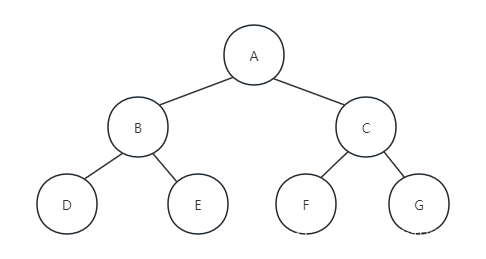
二叉树的中序遍历如何实现呢?别以为很复杂,它和前序遍历其实就是代码顺序上的差异:
void InOrderPraverse(BiTree T)
{if(T==NULL)return;InOrderPraverse(T->lchild);printf("%c",T->data);InOrderPraverse(T->rchild);
}换句话说,它等于把调用左孩子的递归函数提前了,就这么简单,我们来看看调用InOrderPraverse(T)函数时,程序是如何运行的呢?
(1)调用PreOrderTraverse(T),T的根节点不为NULL,于是调用PreOrderTraverse(T->lchild),访问B节点,当前指针仍不为NULL,继续调用PreOrderTraverse(T->lchild),访问节点D,继续调用PreOrderTraverse(T->lchild),访问D节点的左孩子,发现当前指针为NULL,于是返回,打印当前节点D,如下图所示:
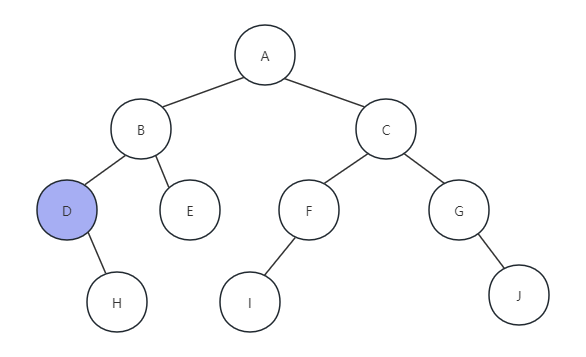
(2)然后调用PreOrderTraverse(T->rchild),访问节点D的右孩子H,因为H也没有左孩子,所i打印H,如下图所示:
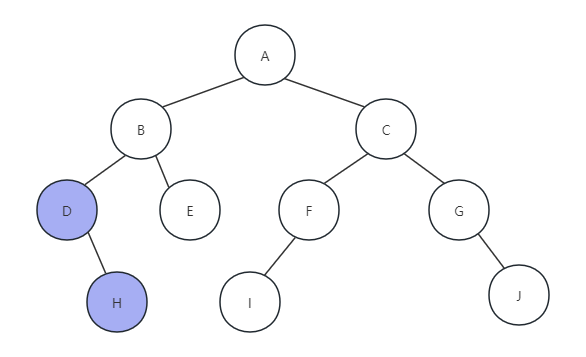
(3) 因为H节点没有右孩子,所以返回,打印节点D函数执行完毕,返回打印字母B,如下图所示:
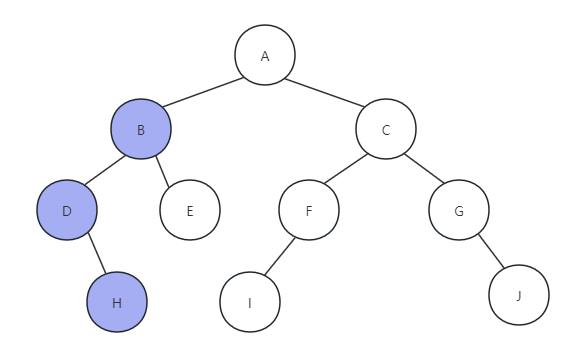
(4)调用PreOrderTraverse(T->rchild),访问B节点的右孩子,因为E节点没有左孩子,所以打印字母E,如下图所示:
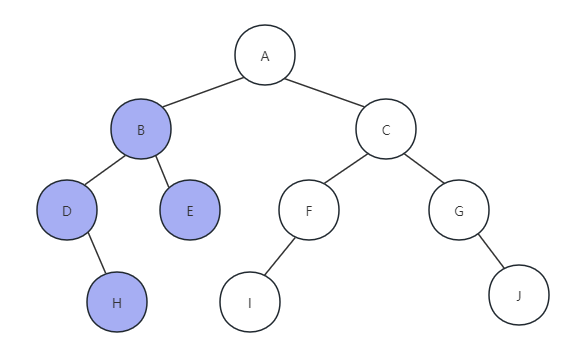
(5)E节点没有右孩子,返回,节点B的递归函数执行完毕,返回到我们最初调用InOrderPraverse的地方,打印字母A,如下图所示:

(6)再调用PreOrderTraverse(T->rchild),访问A节点的右孩子C,再递归访问C节点的左孩子F,接着访问节点F的左孩子I,因为I没有左孩子,打印I,之后分别打印F、C、G、J。这里具体步骤也就省略了。
综上所述,中序遍历这棵二叉树的节点顺序为:D、H、B、E、S、A、I、F、C、G、J。
2.3后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后节点地方式遍历访问左右子树,最后访问根节点,即按照“左子树-右子树-根节点”的顺序遍历二叉树。如下图所展示的二叉树,遍历的顺序为DEBFCGA:
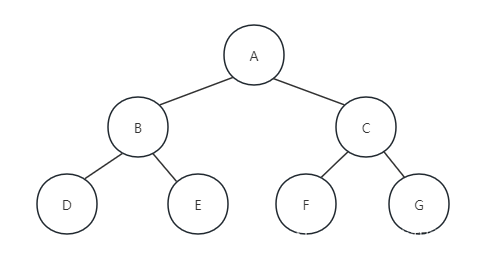
同样地,后序遍历也就很容易想到应该如何写代码了:
void PostOrderPraverse(BiTree T)
{if(T==NULL)return;PostOrderPraverse(T->lchild);PostOrderPraverse(T->rchild);printf("%c",T->data);
}如下图所示,后序遍历是先递归左子树,由根节点A->B->D,节点D没有左孩子,再查看节点H,因为节点H没有左右孩子,所以打印字母H,返回
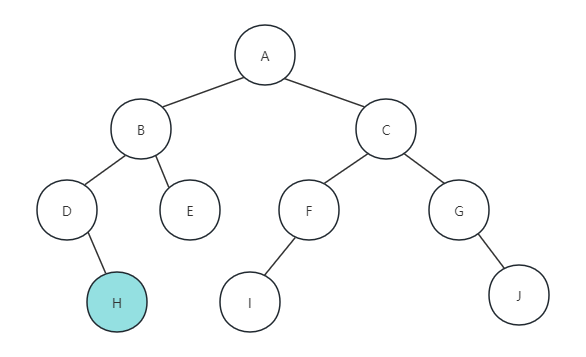
最终,后序遍历地节点的顺序为H、D、E、B、I、F、J、G、C、A,可以完全参考前面的两个遍历方法来得到这个结果。
2.4层序遍历
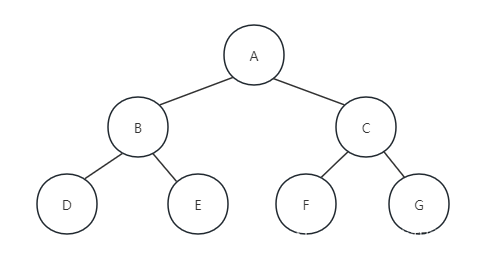
规则是若树为空,则空操作返回,否则从树的第一层,也就是从根节点开始访问,从上而下逐层遍历,在同一层中,按从左到右地顺序对节点逐个访问。如下图所示:遍历地顺序为ABCDEFG。
2.5推到遍历的结果
有一种题目为了考察我们对二叉树遍历的掌握程度,是这样出题的:已知一棵二叉树的前序遍历序列为ABCDEF,中序遍历序列为CBAEDF,请问这棵二叉树的后序遍历结果是多少?
对于这样的题目,如果真的完全了解了前中后序地原理,是不难滴。三种遍历都是从根节点开始的,前序遍历是先打印再递归左和右。所以前序遍历序列为ABCDEFG,第一个字母是A被打印出来,就说明A是根节点的数据,再由中序遍历序列是CBAEDF,可以知道C和B是A左子树的节点,E、D、F是A右子树的节点,如下图所示:

然后我们看前序中的C和B,他的顺序是ABCDEF,是先打印B后打印C,所以B应该是B地左孩子,而C就只能是B地孩子,此时是左孩子还是右孩子还不确定,再看中序序列是CBAEDF,而C是在B地前面打印,这就说明C是B地左孩子,否则就是右孩子了,如下图所示:

再看前序中的E、D、F,它的顺序是ABCDEF,那就意味着D是A节点的右孩子,E和F是D地子孙,注意,他们中其中一个不一定是孩子,有可能是孙子,再来看中序序列是CBAEDF,由E在D地左侧,而F在右侧,所以可以确定E是D的左孩子,F是D的右孩子。因此最终得到的为叉树如下图所示:
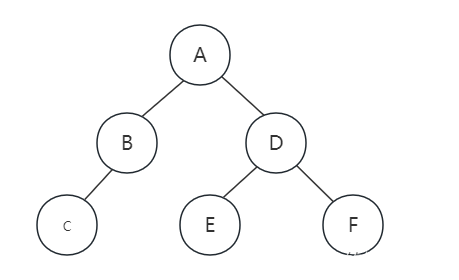
为了避免推到中的失误,最好在心中递归遍历,检查一下这棵树的前序和中序遍历序列是否与题目中的相同,已经恢复了二叉树,要获得他的后序遍历结果就是易如反掌,结果就是CBEFDA。
反过来,如果我们的题目是这样:二叉树的中序序列是ABCDEFG,后序序列是BDCAFGE,求前序序列。
这次简单,由后序的BDCAFGE,得到E是根节点,因此前序首字母是E。于是根据中序序列分为两棵树ABCD和FG,由后序序列的BDCAFGE,知道A是E的左孩子,前序序列目前分析为EA。再由中序序列的ABCDEFG,知道BCD是A节点的右子孙,再由后序序列的BDCAFGE知道C节点是A节点的右孩子,前序序列目前分析得到EAC。由中序序列ABCDEFG,得到B是C的右孩子,所以前序序列目前分析为EACBD,由后序序列BDCAFGE,得到G是E的右孩子,于是F就是G的孩子,而且还是左孩子,前序遍历序列的最终结果就是EACBDGF。
从这里我们也得到了两个二叉树遍历的性质:
- 已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
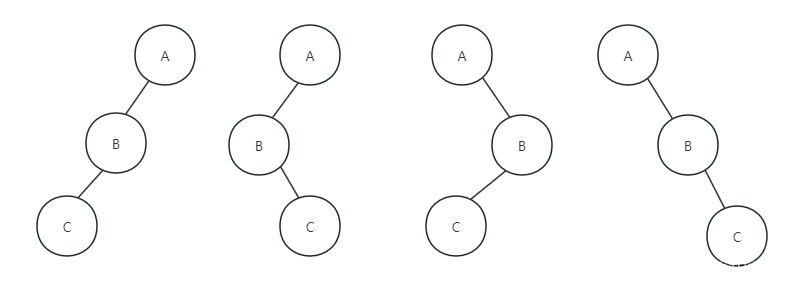
但是要注意了,已知前序和后序遍历,是不能确定一棵二叉树的,原因也很简单,比如前序序列是ABC,后序序列是CBA,我们可以确定A一定是根节点,但接下来,我们无法知道,哪个节点是左子树,哪个节点是右子树,这棵树可能有如下图所示的四种可能:
3.二叉树的建立
说了半天,我们该如何在内存中生成一棵二叉链表的二叉树呢?如果我们要在内存中建立一个左下角这样的树,为了能让每个节点确认是否存在有左右孩子,我们对它进行了拓展,变成右下角的样子,也就是将二叉树中的每个结点的空指针引出一个虚结点,其值为一特定值,比如“#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树,比如左下角的前序遍历序列为AB#D##C##。

有了这样的准备,我们就可以把刚才前序遍历的序列AB#D##C##用键盘挨个输入,实现代码如下:
void CreateBiTree(BiTree* T)
{TDataType ch;scanf("%c",&ch);ch=str[index++];if(ch=='#')*T=NULL;else{*T=(BiTree)malloc(sizeof(BiTree));if(!*T)exit(-1);(*T)->data=ch;CreateBiTree(&(*T)->lchild);CreateBiTree(&(*T)->rchild);}
}