LeetCode 算法：旋转图像c++

原题链接🔗：旋转图像
难度：中等⭐️⭐️

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1：
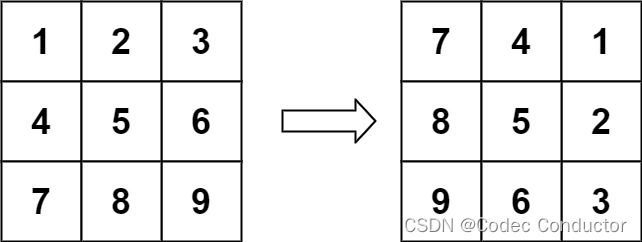
在这里插入图片描述
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：
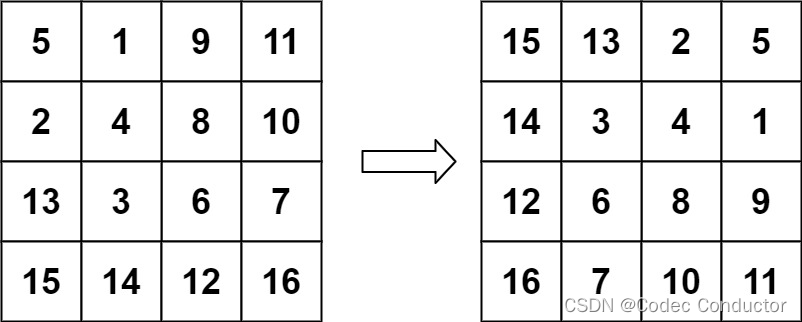
在这里插入图片描述
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

题解

辅助数组法

题解:

要将一个 n × n 的二维矩阵（代表一个图像）顺时针旋转 90 度，你可以遵循以下解题思路：

理解问题：首先，理解顺时针旋转90度意味着什么。对于矩阵中的每个元素，它将移动到原始位置的左上角方向。

创建新矩阵：由于旋转后的矩阵大小不会改变，你可以使用与原始矩阵相同大小的新矩阵来存储结果。

遍历原始矩阵：遍历原始矩阵的每个元素，确定它们在新矩阵中的位置。对于矩阵中的每个元素 matrix[i][j]，它将在新矩阵中的位置是 new_matrix[j][n-1-i]。

填充新矩阵：按照上述规则，将原始矩阵的元素复制到新矩阵的相应位置。

优化空间：如果不需要保留原始矩阵，你可以在原地修改矩阵以节省空间。这可以通过先交换行，然后反转每一行来实现。

代码实现：根据上述逻辑，编写代码实现矩阵的旋转。

测试：编写测试用例来验证你的解决方案是否正确。确保测试包括各种大小的矩阵，包括特殊情况，如 n=1 或 n=2。

考虑边界条件：确保你的解决方案能够处理矩阵的边界条件，例如矩阵的第一行和第一列。

性能分析：分析你的解决方案的时间和空间复杂度。理想情况下，时间复杂度应该是 O(n^2)，因为每个元素都被访问一次，空间复杂度应该是 O(1)，如果原地旋转的话。

代码优化：如果可能，尝试优化你的代码，使其更简洁或提高性能。

以下是一个简化的步骤描述，展示了如何在原地旋转矩阵：

交换矩阵的行和列，即 matrix[i][j] 与 matrix[j][n-1-i] 交换。
反转每一行，即 matrix[i] 变为 matrix[i] 的逆序。

这种方法不需要额外的空间，因为它直接在原始矩阵上进行操作。但请注意，这种方法会修改原始矩阵，如果需要保留原始矩阵，则需要先复制一份。

复杂度：时间复杂度应该是 O(n²)，时间复杂度应该是 O(n²)。
过程：

创建一个新的 n × n 的矩阵，用于存储旋转后的图像。
遍历原始矩阵，对于每个元素matrix[i][j]，将其复制到新矩阵的相应位置，使用公式 new_matrix[j][n-1-i]。
释放原始矩阵（如果需要的话）。

c++ demo：

#include <iostream>
#include <vector>using namespace std;void rotateMatrix(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> newMatrix(n, vector<int>(n));// 将原始矩阵的元素复制到新矩阵中for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {newMatrix[j][n - 1 - i] = matrix[i][j];}}// 将新矩阵赋值回原始矩阵matrix = newMatrix;
}void printMatrix(const vector<vector<int>>& matrix) {for (const auto& row : matrix) {for (int val : row) {cout << val << " ";}cout << endl;}
}int main() {vector<vector<int>> matrix = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};cout << "Original Matrix:" << endl;printMatrix(matrix);rotateMatrix(matrix);cout << "Rotated Matrix:" << endl;printMatrix(matrix);cout << endl;vector<vector<int>> matrix2 = {{5,  1,  9,  11},{2,  4,  8,  10},{13, 3,  6,  7 },{15, 14, 12, 16}};cout << "Original Matrix2:" << endl;printMatrix(matrix2);rotateMatrix(matrix2);cout << "Rotated Matrix2:" << endl;printMatrix(matrix2);return 0;
}

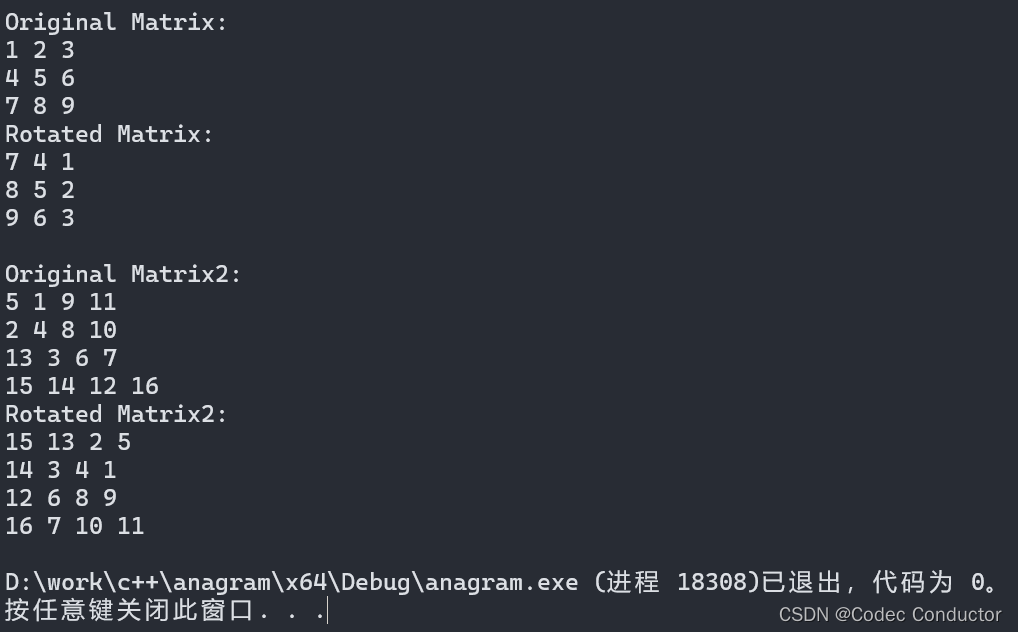
输出结果：

Original Matrix:
1 2 3
4 5 6
7 8 9
Rotated Matrix:
7 4 1
8 5 2
9 6 3

Original Matrix2:
5 1 9 11
2 4 8 10
13 3 6 7
15 14 12 16
Rotated Matrix2:
15 13 2 5
14 3 4 1
12 6 8 9
16 7 10 11