理解数学概念——线性(线性性)

1. 线性相关词汇的词源

1.1 单词“line”的词源

这个单词是古英语“line”和古法语“ligne”二者的融合。在古英语中，“line”的词义为“缆绳，绳索；一系列，行，字母行；规则，方向(cable, rope; series, row, row of letters; rule, direction)，” 而在古法语中，“ligne”的记义为“指南，绳索，线；世系，下降(guideline, cord, string; lineage, descent)，”(约12世纪时) 而这两个词都来自拉丁语“linea”,词义为“亚麻线、细绳、铅垂线(linen thread, string, plumb-line)，” 另外的词义为“标记、界限、极限、目标；下降线(a mark, bound, limit, goal; line of descent),” 是“linea restis”(词义为“linen cord”)的简写。

中世纪英语中最早的含义是“建筑工人用来测量的绳索”；14 世纪晚期扩展为“线状标记”(源自“建筑工人用来使物体平整的绳索”，14 世纪中期)，也指“轨道、路线、方向”。含义(郡县等的)“界限、边界”来自 1590 年代。数学含义“不计宽度的长度”来自 1550 年代。1530 年代起扩展为“手掌或脸部的褶皱”。1580 年代起扩展为“赤道(the equator)”。

“排列成直线的事物或人”的词义源自 1550 年代。现在被认为是美式英语，其中英式英语同义词使用队列(queue)一词，但该意思最早出现在英语作家作品中。“按时间顺序连续的人”(世系国王等)的词义源自 14 世纪晚期。

词义“某人的职业，业务部门”源自 17 世纪 30 年代，根据牛津英语辞典，可能源自对《哥林多后书》第 10.16 章被误解的 KJV 译本，“并且不要在别人为我们准备好的东西上吹嘘(And not to boast in another mans line of things made ready to our hand)”，其中的“line”翻译为希腊语“kanon”，可能意味着“边界，限制”；短语“in another man's line”是括号内的。

1.2 单词“linear”的词源

“linear”是一个形容词，词义为“类似一条线的，关于或属于线的，” 来自法语“linéaire”，该法语词又派生自拉丁词“linearis”，其在拉丁语中的词义为“属于线的”，派生自另一个拉丁语“linea”，词义为“串，线(string,line)，” 其词源同“line”的词源。在本质上，“linear”与“lineal”是同一个词；在拉丁语中，“linearis”最初的后缀是“-alis”，后来被消化吸引为“-aris”，但在晚期拉丁语中，这种规则不再有构词能力，因此构词成分以“-aris”保持不变。

1.3 单词“linearity”的词源

单词“linearity”由形容词“linear”+“-ity”(形容词构成名词的构词成分)构成，在数学中译为“线性性”。

2. “线性”的词典解释

牛津英语词典(OED)对“linear”的解释：“Having the direction of a line; extended in a line or in length; spec. in Math. and Phys. involving measurement in one dimension only;capable of being represented by a straight line on a graph(in Cartesian co-ordinates);involving or possessing the property that a change in one quantity is accompanied by or corresponds to a directly proportional chnage in a related one.linear equation,an equation of the first degree.”(具有线的方向(即向两端的方向)；按线或按长度的方式延伸(不考虑宽度)；特别是在数学和物理学中，仅按一维的方式进行度量；能够用图上的直线表示(在笛卡尔坐标中)；涉及或拥有这样的特性：一个量的变化伴随或对应于相关量以常比的方式进行相应变化。线性方程(一次方程))。

3. “线性”的数学意义

从以上2的解释可以看出，“线性”在数学中的含义是由“线”引申而来的，即这种伴随的变化关系是按“线”的方式延伸的，向两站延伸。在数学中更进一步地引申为“按直线的两端延伸”的关系。这种关系可以在笛卡尔坐标图中用直线体现出来，其体现出来的特性就是：一个量的变化伴随着或对应于相关量以常比的方式进行相应的变化。

4. 数学中的线性概念

4.1 线性代数(Linear algebra)

4.1.1 关于“线性代数”这一术语的一些历史

DSB(Dictionary of Scientific Biography)似乎表明，术语“线性代数(algebra linearia)”由Rafael Bombelli (1526-1572)在其《代数学》第四卷中使用，指代几何方法在代数中的应用。

在英语中，“线性代数(linear algebra)”一词最早出现在1870 年的《美国数学杂志》(American Journal of Mathematics)(1881年)4页，107页中：“An algebra in which every expression is reducible to the form of an algebraic sum of terms, each of which consists of a single letter with a quantitative coefficient, is called a linear algebra(如果一个代数中的每个表达式都可以简化为项的代数和的形式，并且每个项都由一个带有定量系数的单个字母组成，则这种代数称为线性代数)。”[牛津英语辞典]。

“线性代数”一词于1875 年出现在一篇标题为“论线性代数的用途和变换(On the uses and transformations of linear algebra)”的文章标题中，作者是Benjamin Peirce，发表于《美国科学院院刊》(American Acad. Proc. 2)。

Pierce的意思是今天我们所说的“域上的有限维代数”，而不是向量空间和线性变换的理论。

1898 年，Alfred North Whitehead 在《通用代数及其应用》(A Treatise on Universal Algebra with applications)的脚注中写道：“Grassman (参见 Audehanungelebre vom 1862, §50) 将乘法类型称为‘线性(linear)’。”但这种命名法与 B. Peirce 在其关于线性结合代数的论文《美国数学杂志》第 IV 卷 (1881) 中定义的‘线性代数’的普遍接受含义相冲突。第 (2) 节的定理是Grassman提出的，参见同上。”

4.1.2 线性代数的定义

线性代数是数学学科的一个分支，它关注的是形如

$a_{1} x_{1} + ...+ a_{n} x_{n} = b$

的线性方程(linear equations)(注：这些变量之间的变化关系是常比的)，和形如

$( x_{1} ,..., x_{n} ) \longmapsto a_{1} x_{1} + ...+ a_{n} x_{n}$

的线性映射(linear maps)(注：这种映射关系也是常比的)，以及它们在向量空间中和通过矩阵的表示。

线性代数是几乎所有数学领域的核心。例如，线性代数是现代几何学的基础，包括定义线、平面和旋转等基本对象。此外，数学分析的一个分支——泛函分析(functional analysis)，也可以看作是线性代数在函数空间中的应用。

线性代数也用于大多数科学和工程领域，因为它可以对许多自然现象进行建模，并利用这些模型进行高效计算。对于无法用线性代数建模的非线性系统，它通常用于处理一阶近似，利用这样一个事实：多元函数在某一点的微分是该点附近最接近该函数的线性映射。

4.2 线性编码(Linear code)

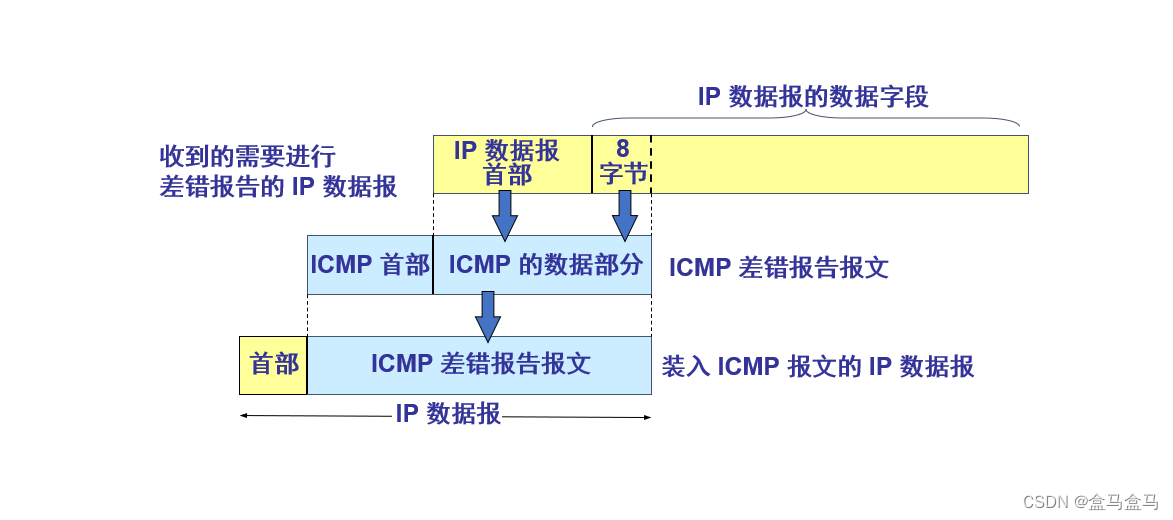
在编码理论中，线性编码是一种纠错码，任何码字(codewords)的线性组合也是码字。线性码传统上分为分组码和卷积码，尽管 Turbo 码可以看作是这两种类型的混合。与其他码相比，线性码允许更高效的编码和解码算法。

线性编码用于前向纠错，并应用于在通信信道上传输符号(例如，位(bits))的方法，这样，如果通信中出现错误，消息块的接收者可以纠正或检测一些错误。线性分组码中的码字是使用比要发送的原始值更多的符号进行编码的符号块。

4.3 线性密码学分析(Linear cryptanalysis)

在密码学中，线性密码分析是一种基于寻找密码行为的仿射近似的密码分析的通用形式。已经开发了针对分组密码和流密码的攻击。线性密码分析是两种最广泛使用的分组密码攻击之一；另一种是差分密码分析。

这一发现归功于松井满，他首次将该技术应用于 FEAL 密码(松井和山岸，1992 年)。随后，松井发表了对数据加密标准 (DES) 的攻击，最终导致公开社区报告了对该密码的首次实验性密码分析(松井，1993 年；1994 年)。对 DES 的攻击通常不切实际，需要 247 个已知明文。

有人提出了各种改进攻击的方法，包括使用多重线性近似或结合非线性表达式，从而实现广义分区密码分析。新密码设计通常需要有对抗线性密码分析的安全性证据。

4.4 线性方程(Linear equations)

形如 $a_{1} x_{1} + ...+ a_{n} x_{n} + b = 0$ 的方程称为线性方程，其中， $x_{1} ,..., x_{n}$ 是变量(或未知数)，而 $b ,a_{1} ,..., a_{n}$ 是系数(通常是实数)。可将系数看成是方程的参数，且可以是任意表达式(假设他们不包括任意变量)。为了产生有意义的方程，要求系数 $a_{1} ,..., a_{n}$ 不能全为零。

或者，可以通过将某个域上的线性多项式等于零来获得线性方程，并从中取出系数。这种方程的解就是当代入未知数时使等式成立的值。

如果只有一个变量，则只有一个解(假设 $a_{1} \neq 0$ )。通常，术语“线性方程”默认指这种特殊情况，其中变量被合理地称为未知数。

对于两个变量的情况，每个解都可以解释为Euclid平面上一个点的笛卡尔坐标。线性方程的解在Euclid平面上形成一条直线，反过来，每条直线都可以看作是两个变量的线性方程的所有解的集合。这就是描述这种方程的术语“线性”的起源。更一般地说，n 个变量的线性方程的解在 n 维Euclid空间中形成一个超平面(hyperplane)(n − 1 维的子空间)。

线性方程在所有数学及其在物理学和工程学中的应用领域中频繁出现，部分原因是非线性系统通常可以用线性方程很好地近似。

4.5 线性函数(Linear functions)

在数学中，术语“线性函数”指的是两个不同但相关的概念：

(1) 在微积分和相关领域中，线性函数是图像为直线的函数，即零次或一次多项式函数。为了将这种线性函数与其他概念区分开来，通常使用术语仿射函数(affine function)(译注：相似映射，即线性变换接一个平移)。

(2) 在线性代数、数学分析和泛函分析中，线性函数是线性映射。

4.6 线性泛函(Linear functional)

在数学中，线性形式(也称为线性泛函、一元形式或余向量(covector))是从向量空间到其标量场(field)(通常是实数或复数)的线性映射。

4.7 线性映射(Linear map)

在数学中，更具体地说在线性代数中，线性映射(也称为线性映射(a linear mapping)、线性变换、向量空间同态(vector space homomorphism)，或在某些情况下称为线性函数）是两个向量空间之间的映射 𝑉 → 𝑊，它保留了向量加法和标量乘法的运算。相同的名称和相同的定义也用于环上模的更一般情况；参见模同态。

4.8 线性规划(Linear programming)

线性规划(LP)，也称为线性优化(linear optimization)，是一种在数学模型中实现最佳结果(例如最大利润或最低成本)的方法，其要求和目标由线性关系表示。线性规划是数学规划(也称为数学优化)的一个特例。

更正式地说，线性规划是一种优化线性目标函数的技术，受线性等式和线性不等式约束。其可行域是凸多面体，该多面体是定义为有限多个半空间的交集的集合，每个半空间都由线性不等式定义。其目标函数是在此多面体上定义的实值仿射(线性)函数。如果存在这样的点，线性规划算法会在多面体中找到此函数具有最大(或最小)值的点。

4.9 线性系统(Linear system)

在系统理论中，线性系统是基于使用线性算子的系统的数学模型。线性系统通常表现出比非线性[需要消除歧义]情况简单得多的特征和属性。作为数学抽象或理想化，线性系统在自动控制理论、信号处理和电信领域有着重要的应用。例如，无线通信系统的传播介质通常可以用线性系统建模。

4.10 线性方程组(System of linear equations)

在数学中，线性方程组(或线性系统)是涉及相同变量的一个或多个线性方程的集合。例如，

$\left \{ \begin{array}{rlc} 3x+2y-z=1 \\ x-y+2z=-1 \\ -x+\frac{1}{2}y-z=0 \end{array} \right.$

是三个变量 x、y、z 的三个方程组。线性系统的解是将值分配给变量，使得所有方程同时满足。在上面的例子中，解由有序三元组 (x, y, z) = (1 ， -2 ， -2 )给出，因为它使得所有三个方程都有效。

线性系统是线性代数的一个基本部分，线性代数是大多数现代数学中使用的一门学科。用于寻找解决的计算算法是数值线性代数的重要组成部分，在工程、物理、化学、计算机科学和经济学中发挥着重要作用。非线性方程组通常可以用线性系统来近似(参见线性化)，这是一种在建立数学模型或计算机模拟相对复杂系统时非常有用的技术。