1. 简介
Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德的名字命名。
2. 核心思想
通过考虑图中所有可能的中转点,逐步更新两点间的最短路径长度和路径信息,直至找到最终的最短路径。有的人也称之为插点法。
3. 图解
3.1 初始化
初始化:设置图的邻接矩阵dict,其中dict[i][j]表示顶点i到顶点j的直接路径权重;如果两顶点不直接相连,则设为无穷大INF。
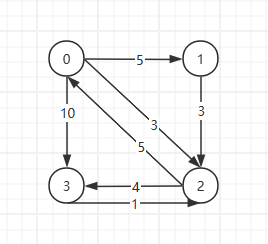
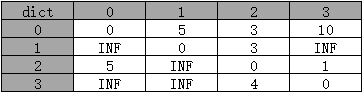
3.2 更新最短路径
更新最短路径:把每个节点当作是中转节点,更新矩阵中的距离。
通过中间顶点 k 从顶点 i 到顶点 j 的距离 小于 直接从顶点 i 到顶点 j 的距离,更新 dist[i][j] = dist[i][k] + dist[k][j]。
把0作为中转节点,此时表中黄色部分是不需要改的(都是从0出发或是直接到0的距离),
当更新 dict[1][2]也就是1 -> 2 时,需判断 1 -> 0 和 0 -> 2 的和是否比直达的1 -> 2更小。
若路径中有INF就无需更新,比如此时1 -> 0 就是INF,表示1 -> 2 以 0 作为中转点时不可能比 1 -> 2 直达的更小,所以此时不需要更新。
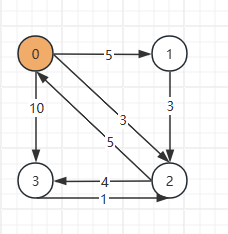
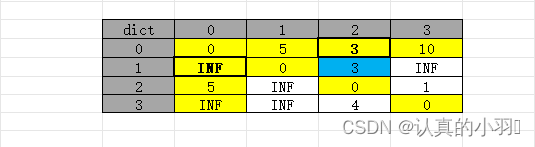
更新完 0作为中转节点时 数组为:

更新完 1作为中转节点时 数组为:
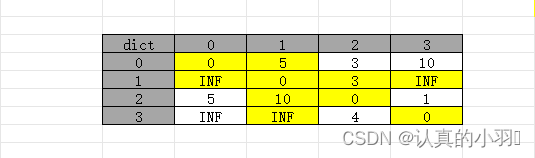
更新完 2作为中转节点时 数组为:

更新完 3作为中转节点时 数组为:

3.3 结果
最终结果的数组中就是点到点的最短路径。
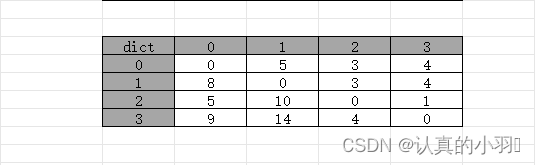
4. 代码实现
定义了一个4x4的图,其中INF表示两个顶点之间没有直接相连的边。然后调用floyd方法计算所有顶点对之间的最短路径,并输出结果。
public class Floyd {private static final int INF = Integer.MAX_VALUE; public static void floyd(int[][] graph) {int n = graph.length; // 获取图的顶点数int[][] dist = new int[n][n]; // 初始化矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dist[i][j] = graph[i][j]; }}// 使用Floyd算法计算所有顶点之间的最短路径for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][k] != INF && dist[k][j] != INF&& dist[i][k] + dist[k][j] < dist[i][j]) { // 更新i到j的最短路径dist[i][j] = dist[i][k] + dist[k][j];}}}}// 输出所有顶点之间的最短路径for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.print(dist[i][j] + " ");}System.out.println();}}public static void main(String[] args) {int[][] graph = {{0, 5 , 3 , 10 },{INF, 0 , 3 , INF},{5 , INF, 0 , 1 },{INF, INF, 4 , 0 }};floyd(graph); }
}
5. floyd算法和Dijkstra算法的区别
Floyd算法和Dijkstra算法都是计算图中顶点之间最短路径的著名算法,但它们的应用场景、原理和性能存在显著差异。具体分析如下:
应用场景
- Dijkstra算法:适用于单源最短路径问题,即从单个源点到其他所有点的最短路径。它不能处理具有负权边的图。
- Floyd算法:用于求解任意顶点对(多源最短路径问题)的最短路径,可以处理负权边,但不能处理包含负权回路的图。
算法原理
- Dijkstra算法:基于贪心策略,每次从未确定的顶点中选择一个距离源点最近的顶点,然后更新其邻接顶点的距离。该算法需要使用优先队列来选择下一个顶点,并且初始时除源点外的所有顶点的距离都设置为无穷大。
- Floyd算法:通过动态规划的方式,利用三层嵌套循环来计算所有顶点对之间的最短路径。算法的基本操作是比较(u,k) + (k,v)与(u,v)的长度,并据此更新(u,v)的长度。
时间复杂度
- Dijkstra算法:使用优先队列优化后的时间复杂度是O((V+E) log V),其中V是顶点数,E是边数。如果使用邻接矩阵实现且没有优化,复杂度会是O(V^2)。
- Floyd算法:时间复杂度为O(V^3),因为算法需要三层循环遍历所有顶点对和可能的中间顶点。
额外功能
- Dijkstra算法:可以输出从源点到各顶点的最短路径。
- Floyd算法:可以输出任意两个顶点间的最短路径及其长度。
总之,Dijkstra算法适合解决单源最短路径问题,尤其是在没有负权边的情况下,而Floyd算法适合解决所有顶点对之间的最短路径问题,尽管它可以处理负权边的情况,却不能容忍负权回路的存在。
6. 总结
总的来说,Floyd算法是一种计算图中所有顶点对之间最短路径的动态规划算法,它能够处理包含负权边的图,但不允许存在负权回路。适用于小型到中等规模稠密图的算法,尤其是在需要全局最短路径信息时。对于大型稀疏图或者单源最短路径问题,其他算法如Dijkstra算法可能更加合适。





![[2024-06]-[大模型]-[DEBUG]- ollama webui 11434 connection refused](https://img-blog.csdnimg.cn/direct/b3e2eea302d64b04a52afde4f26d32c2.png)