目录
一、实验目的
二、实验概述
三、实验内容
四、问题描述
1.实验基本要求
2.实验亮点
3.实验说明
五、算法原理和实现
问题1-4算法
1. 选择排序
算法实验原理
核心伪代码
算法性能分析
数据测试
选择排序算法优化
2. 冒泡排序
算法实验原理
核心伪代码
算法性能分析
数据测试
3. 快速排序
算法实验原理
核心伪代码
算法性能分析
数据测试
4. 合并排序
算法实验原理
核心伪代码
算法性能分析
数据测试
优化模型
5. 插入排序
算法实验原理
算法性能分析
数据测试
问题5算法
方法一: 排序查找
方法二: 选择查找
方法三: 优先队列
六、实验结果和分析
七、实验结论
一、实验目的
1、掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理
2、掌握不同排序算法时间效率的经验分析方法,验证理论分析与经验分析的一致性。
二、实验概述
排序问题要求我们按照升序排列给定列表中的数据项,目前为止,已有多种排序算法提出。本实验要求掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理,并进行代码实现。通过对大量样本的测试结果,统计不同排序算法的时间效率与输入规模的关系,通过经验分析方法,展示不同排序算法的时间复杂度,并与理论分析的基本运算次数做比较,验证理论分析结论的正确性。
三、实验内容
1、实现选择排序、冒泡排序、合并排序、快速排序、插入排序算法;
2、以待排序数组的大小n为输入规模,固定n,随机产生20组测试样本,统计不同排序算法在20个样本上的平均运行时间;
3、分别以n=10000, n=20000, n=30000, n=40000, n=50000等等,重复2的实验,画出不同排序算法在20个随机样本的平均运行时间与输入规模n的关系,如下图1所示;
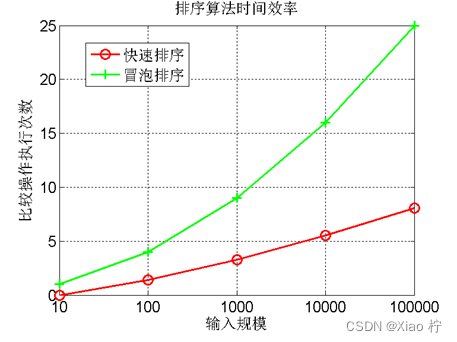
图1. 时间效率与输入规模n的关系图
4、画出理论效率分析的曲线和实测的效率曲线,注意:由于实测效率是运行时间,而理论效率是基本操作的执行次数,两者需要进行对应关系调整。调整思路:以输入规模为10000的数据运行时间为基准点,计算输入规模为其他值的理论运行时间,画出不同规模数据的理论运行时间曲线,并与实测的效率曲线进行比较。经验分析与理论分析是否一致?如果不一致,请解释存在的原因。
5、现在有10亿的数据(每个数据四个字节),请快速挑选出最大的十个数,并在小规模数据上验证算法的正确性。
四、问题描述
1.实验基本要求
①.实现选择排序、冒泡排序、合并排序、快速排序、插入排序五大排序算法的算法实现原理
②.计算各个排序在不同规模下算法的运行时间,并画出理论分析效率分析的曲线和实测的效率曲线,比较经验分析和理论分析是否一致并给出原因
③.根据排序在不同规模下算法的运行时间,画出不同排序算法在20个随机样本的平均运行时间与输入规模n的关系,并比较各个排序算法之间的优缺点
④.设计算法,使之能从10亿数据中,快速挑选出最大的十个数,并通过小规模数据验证算法的正确性
2.实验亮点
①.实现了对部分算法的优化,在面对大规模数据排序时,合并排序以及快速排序可以发挥很大的作用
②.成功实现从10亿数据中快速挑选最大的十个数
③.对实验过程中发现的相关问题进行了探究并解决
3.实验说明
①.实验结果均以秒为单位,使用双精度浮点数存储
②.相关运行时间仅包括排序程序运行时间,不包括其它时间
③.以输入规模为10000的数据运行时间为基准点,计算输入规模为其他值的理论运行时间
④.所有运行时间都是在测试样本为20的基础下进行平均测量的
五、算法原理和实现
求解问题的算法原理描述,包括算法实现的核心伪代码(不可贴源码)及解释。
问题1-4算法
1. 选择排序
算法实验原理
每次从待排序的序列中找出最小值,存放在序列起始位置继续从剩余未排序元素中寻找最小值,放到已排序列末尾直达全部待排数据排完即可
核心伪代码

算法性能分析
选择排序的外层循环需要进行n次,内部的交换操作介于0与n-1次之间,比较操作介于0与n(n-1)/2次之间,赋值操作介于0与3(n-1)次之间,比较次数为O(n^2)
在最好的情况下,数据已经有序,共交换0次;最坏情况下,交换n-1次,进行n(n-1)次比较;故选择排序的时间复杂度为O(n^2)
数据测试
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 实际 | 0.13825 | 0.5527 | 1.2447 | 2.2526 | 3.59165 |
| 理论 | 0.13825 | 0.553 | 1.24425 | 2.12 | 3.45625 |
根本上述实际运行时间和理论运行时间可以做出下图:
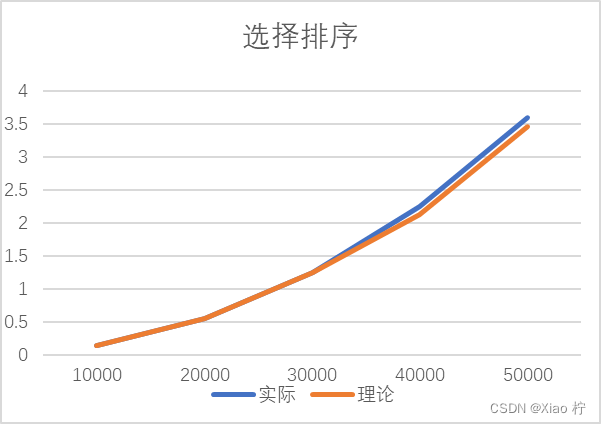
从该图中,我们可以看出,图像基本符合二次增长;
从上表和上图中可以发现整体时间消耗都大致满足数量规模扩大到原来的n倍时,时间消耗扩大n^2的规律
选择排序算法优化
算法每次把数据全部搜索一边,但只排好一个数据,有点太浪费时间了,因此可以将其优化为每次循环找出该序列中的最大最小值,这样每次排好两个数据,可以将循环的次数减少一半,但其算法时间复杂度仍为O(n^2)
改善前与改善后选择排序对于10000-50000数据运行时间如下表所示:
| 数据级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 优化前 | 0.365 | 1.583 | 3.816 | 7.431 | 11.992 |
| 优化后 | 0.332 | 1.467 | 3.645 | 6.9 | 11.051 |
可得图表:
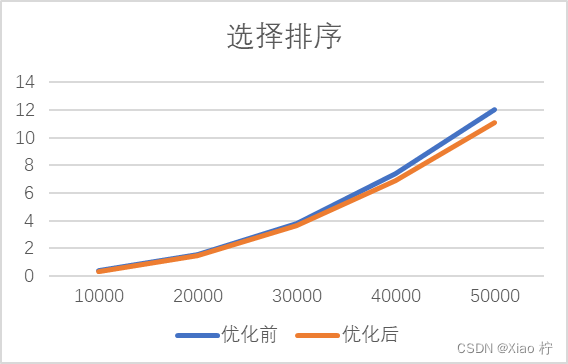
2. 冒泡排序
算法实验原理
从左边开始,依次比较相邻的元素,若左边大于右边,则交换它们的位置继续第一步操作,知道来到数据的右边,此时右边第一个位置 为最大的元素,重复进行直到没有元素需要比较,排序完成
核心伪代码
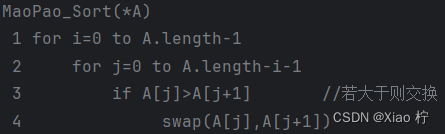
算法性能分析
由伪代码可知,最好情况下,排序前已经有序,只执行一趟,总比较次数为n-1,移动次数为0;最坏情况下,排序前是逆序,则每趟排序都需要比较i-1次并移动i-1次, 总比较次数为n^2/2,总移动次数为n^2/2
在最好的情况下,只需要进行外部循环,时间复杂度为O(n),在最坏的情况下,时间复杂度为O(n^2)
数据测试
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 实际 | 0.36115 | 1.56725 | 3.84645 | 7.3222 | 12.1892 |
| 理论 | 0.36115 | 1.4446 | 3.25035 | 5.7784 | 9.02875 |
根本上述实际运行时间和理论运行时间可以做出下图:
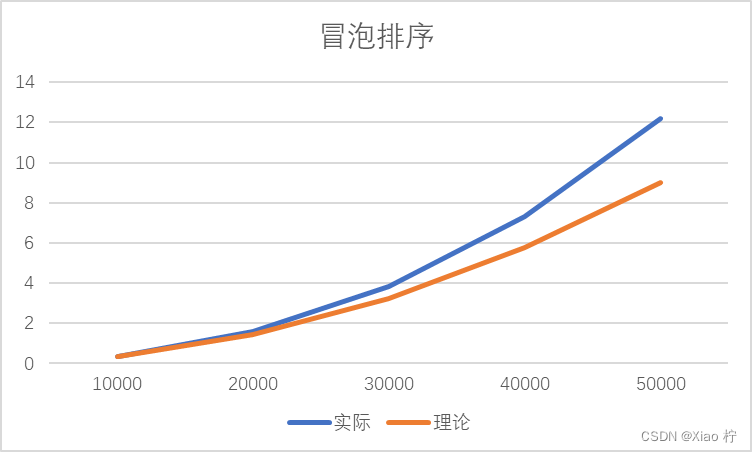
由于冒泡排序算法时间复杂度为O(n^2),故数量级扩大10倍时,时间消耗应扩大100倍。由上图,可得随着数据量的增大,拟合效果越好,所有实验数据符合O(n^2)的时间复杂度。且
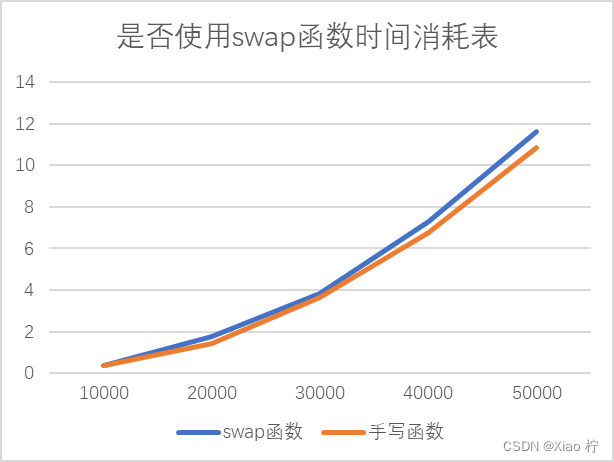
可以看出,当数量级逐渐增大时,实际时间消耗与理论实践消耗有比较大的区别,且随着数量级的增大,彼此之间的区别也越来越大,拟合效果变差。经过分析,选择排序进行了很多次相互调换元素的操作,从而造成元素浪费,因此我进行了两次对比试验,使用库函数 swap函数和手写调换元素的函数进行对比,可以发现在大规模数据的背景下,手写函数的拟合效果更好,性能更优异。
3. 快速排序
算法实验原理
选择一个枢轴元素: 从待排序序列中选择一个元素作为枢轴元素,一般可选择第一个元素或者最后一个元素;借此将该序列分为两个部分:将待排序序列中小于枢轴元素的值放到左边大于枢轴元素的放在右边;再次对左右两部分分别进行快速排序,递归地划分后得到的左右两部分分别进行排序,直到整个序列有序
核心伪代码
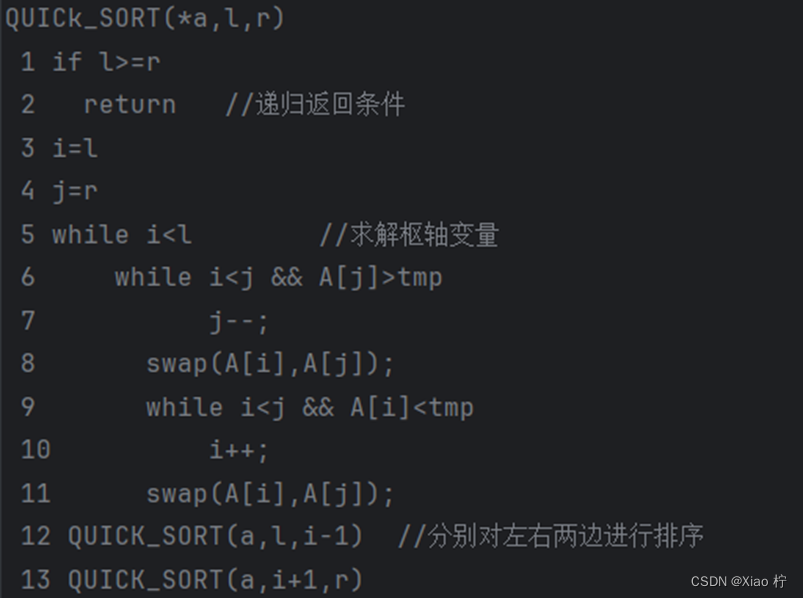
算法性能分析
快速排序的一次划分算法需要两头交替搜索,直到i、j重合,找到一个pivot值,因此该步骤其时间复杂度为O(n),而整个快速排序算法的时间复杂度还与其划分的次数有关。在最好的情况下每次划分几乎都将当前序列等分处理,即仅需经历logn次划分,便可实现子表长度为1,这样,整体的时间复杂度为O(logn*n);在最坏的情况下,每次选的pivot值均为当前序列的最大或最小元素,则需要经历n次划分,才能实现目标,则此时整体的时间复杂度为O(n^2)
综上分析,快速排序的平均时间复杂度为O(n*logn)
数据测试
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 实际 | 0.0014 | 0.00315 | 0.0045 | 0.00685 | 0.0083 |
| 理论 | 0.0014 | 0.00301 | 0.0047 | 0.00644 | 0.0082 |
根本上述实际运行时间和理论运行时间可以做出下图:
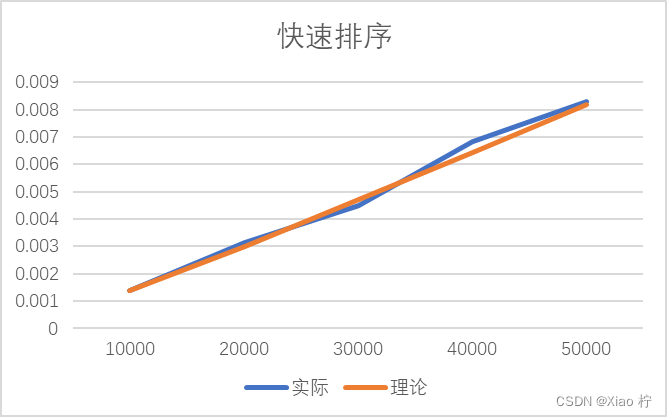
结合上表和上图我们可以看出,整体时间消耗都大致满足O(nlogn)的时间复杂度。且数据拟合效果很好
最差情况下快速排序的表现—当待排数据以逆序顺序待排时,快速排序所用时间与归并排序时间消耗对比,由于栈空间溢出等问题,最大数据我只能测量到30000
| 数量级 | 5000 | 10000 | 15000 | 20000 | 30000 |
| 快速排序 | 0.024 | 0.088 | 0.195 | 0.346 | 0.78 |
| 递归归并排序 | 0.001 | 0.003 | 0.004 | 0.006 | 0.009 |
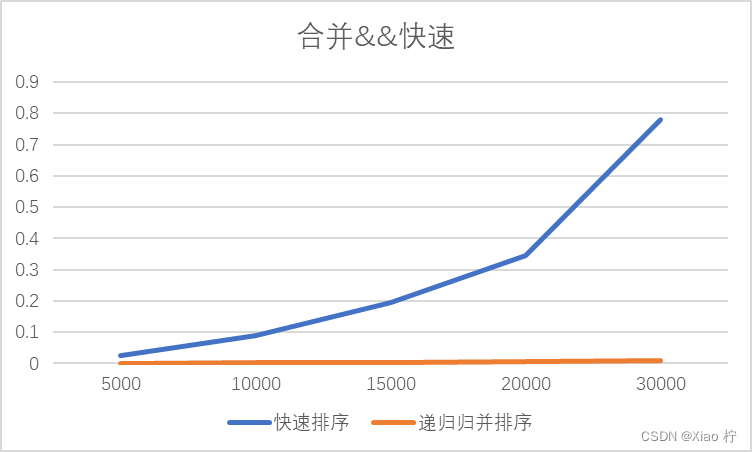
可以看到快速排序时间复杂度退化到O(n^2),运行效率远不如合并排序,每次操作只能够确定一个元素的位置同时进行了n-1次移动,且由于要递归调用n-1次,递归树的深度达到了O(n)
4. 合并排序
算法实验原理
将待排序的线性表不断地切分成若干子表,直到每个子表都只包含一个元素,此时可认为只包含一个元素的子表为有序表,将子表一一合并,每合并一次,就会产生一个新的且更长的有序表,重复操作,直至只剩下一个子表,即为有序表
核心伪代码
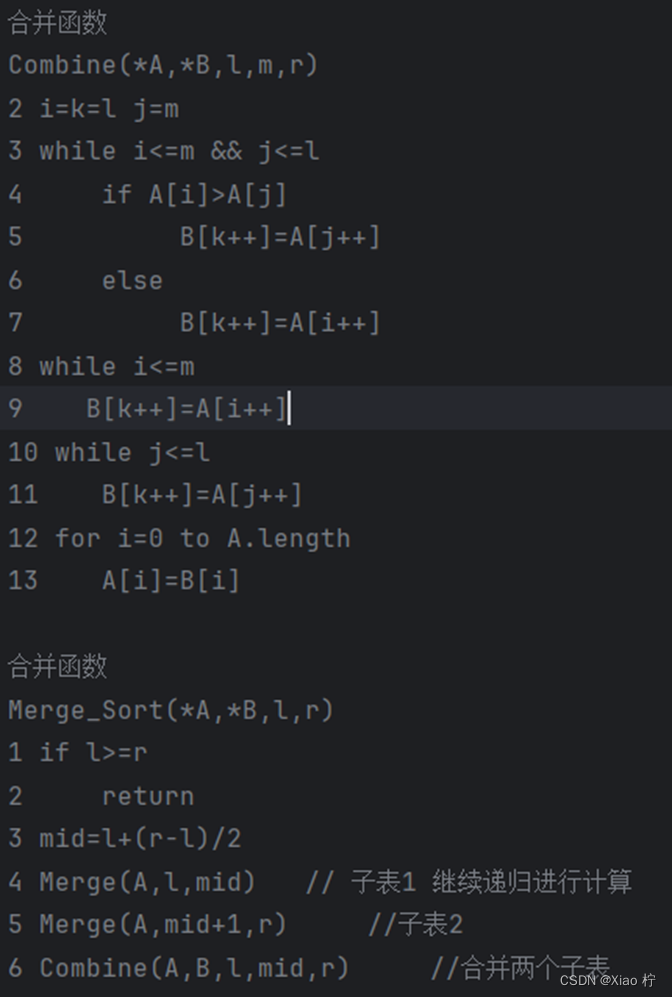
算法性能分析
根据分治法递归,可以求出其递归式:
T(n) = 2* T(n/2) + t
利用主方法,不能求解出其时间复杂度为O(nlogn)
如果待排序的记录为n个,则需要做log2n趟两路归并排序,每趟两路合并排序的时间复杂度为O(n),合并排序的时间复杂度为O(nlog2n),归并排序的空间复杂度是O(n)
数据测试
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 实际 | 0.0038 | 0.0072 | 0.01155 | 0.01565 | 0.0208 |
| 理论 | 0.0038 | 0.0081 | 0.01275 | 0.01748 | 0.0223 |
根本上述实际运行时间和理论运行时间可以做出下图:
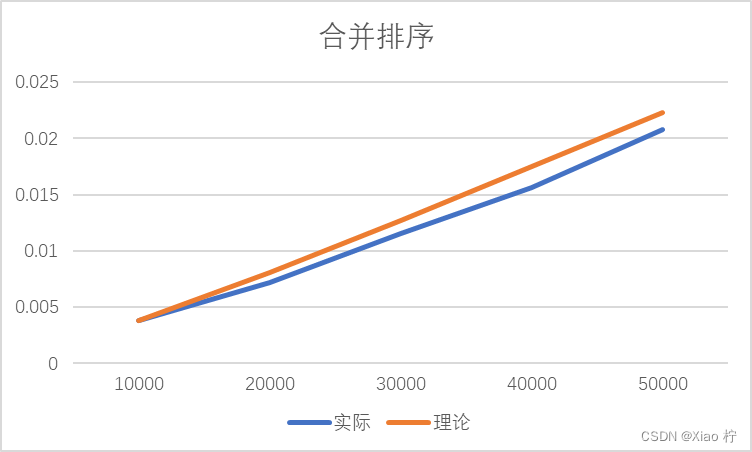
从图像上来看,时间消耗曲线基本是线性的,但其实是因为n的规模还不够大,体现不出对数函数的曲线特性;从数据上来看,规模扩大n2/n1倍,时间扩大为原来的n2/n1*log(2, n2)/log(2, n1)倍,几乎符合,拟合效果比较好,符合时间复杂度为O(nlogn);实际时间消耗曲线一直在理论时间消耗曲线附近波动,其原因为时间级较少,误差较大。
优化模型
非递归实现的合并排序
在上述合并排序的实现中,我采用的是递归实现的合并排序,从存储上看,递归实现的归并其实是对递归树的自顶向下的先序遍历,而非递归归并 是对递归树自顶向下的层次遍历,相对于递归,可以节省大量时间和空间
非递归实现合并排序伪代码

为了验证非递归合并排序算法的优异性,我对比了递归实现以及非递归实现合并排序在面对大规模数据排序时的性能,当测试规模在1000000-10000000变化时,消耗时间如下表所示
| 数量级 | 1000000 | 2000000 | 4000000 | 8000000 | 10000000 |
| 递归实现 | 0.475 | 0.966 | 1.941 | 4.087 | 5.297 |
| 非递归实现 | 0.422 | 0.817 | 1.722 | 3.656 | 4.582 |
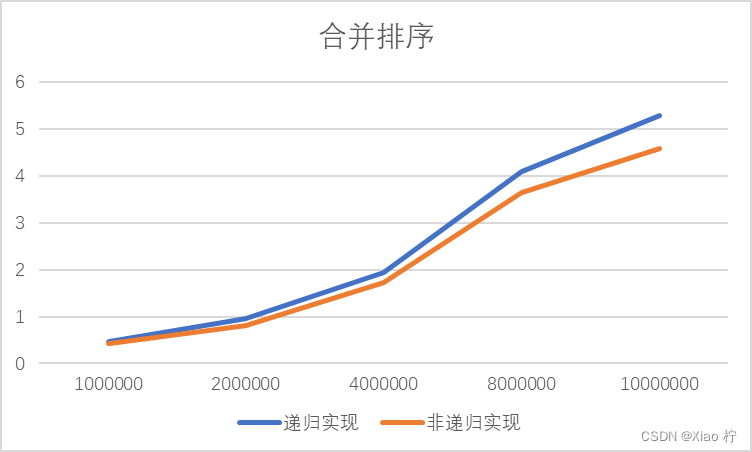
从上图可见,使用非递归实现的时间消耗小于使用递归实现的合并排序,在大规模数据处理中,性能会更加优异
5. 插入排序
算法实验原理
从左边第二个元素开始,向左侧一一比较大小,若比位置元素小,则向左移动,直到该位置上的元素比该元素小,则将元素放在该位置的后一个位置,重复循环,直到右侧元素全部排序完成
核心伪代码
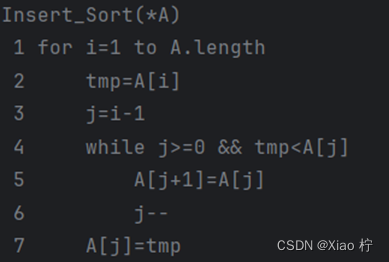
算法性能分析
在最好的情况下,此时整个序列已经有序,只需要进行外部循环,总比较次数为n-1,移动次数为0,此时时间复杂度为O(n); 在最坏的情况下,排序前整个序列为逆序,每趟排序都要比较i-1次并移动i-1次,总比较和移动的次数均为n^2/2
数据测试
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 实际 | 0.10215 | 0.414 | 0.9426 | 1.7219 | 2.7398 |
| 理论 | 0.10215 | 0.4086 | 0.91935 | 1.6344 | 2.55375 |
根本上述实际运行时间和理论运行时间可以做出下图:
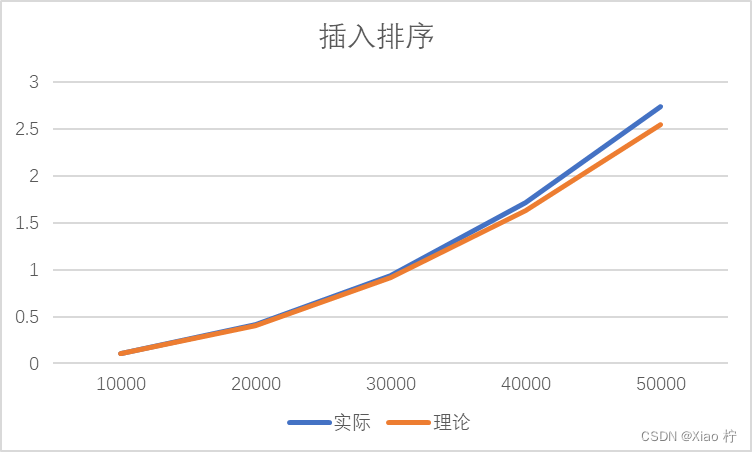
由于插入排序算法时间复杂度为O(n^2),故数量级扩大10倍时,时间消耗应扩大100倍。由上图,可得随着数据量的增大,拟合效果越好,所有实验数据符合O(n^2)的时间复杂度。且图像实际时间消耗曲线与理论时间消耗也基本吻合。
问题5算法
方法一: 排序查找
- 算法实验原理
将全部数据降序排序后,输出前k个数据即可
- 核心伪代码
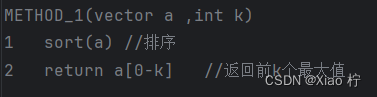
- 算法性能分析
选择归并排序/快速排序,时间复杂度为O(nlogn)
方法二: 选择查找
- 算法实验原理
重复k次循环,每次寻找到最大值后记录,并将其设置为最小值
- 核心伪代码
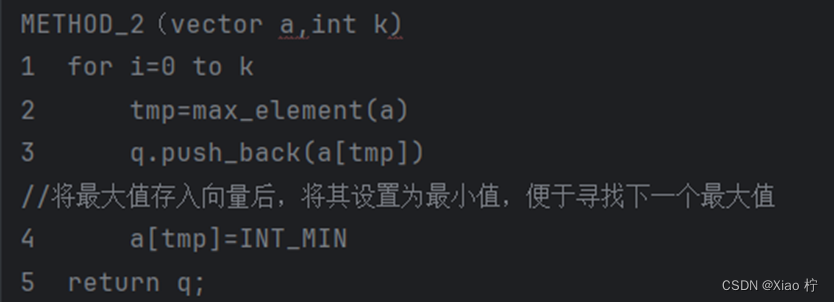
- 算法性能分析
由伪代码可知,算法共需要进行k次循环,其时间复杂度为O(k),其中每次查找最大数都需要遍历整个数据,时间复杂度为O(n),因此,总体时间复杂度为O(kn)
方法三: 优先队列
- 算法实验原理
priority_queue :优先队列是一个具有权值的queue,其内部元素按照元素的权值排列,权值较高者排在最前优先出队,其中缺省情况下系统会通过一个max-heap以堆实现排序特性,表现为vector表现的完全二叉树
限制优先队列的大小为k,当size未达到k时,直接存入,当达到k时,比较其中最小的元素,存储在top上,若大,则先弹出原先数字,并压入该数进优先队列,随后优先队列重新进行内部排序,存储在首位的依旧是十个数中的最小值,便于比较
- 核心伪代码

- 算法性能分析
该算法只需要遍历一次数据,其算法时间复杂度为O(nlogk)
六、实验结果和分析
算法测试结果和效率分析。
问题1-4
五大排序运行时间数据总览
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 选择排序 | 0.13825 | 0.5527 | 1.2447 | 2.2526 | 3.59165 |
| 冒泡排序 | 0.36115 | 1.56725 | 3.84645 | 7.3222 | 12.1892 |
| 合并排序 | 0.0038 | 0.0072 | 0.01155 | 0.01565 | 0.0208 |
| 快速排序 | 0.0014 | 0.00315 | 0.0045 | 0.00685 | 0.0083 |
| 插入排序 | 0.10215 | 0.414 | 0.9426 | 1.7219 | 2.7398 |
将数据可视化,做成图表如下所示:
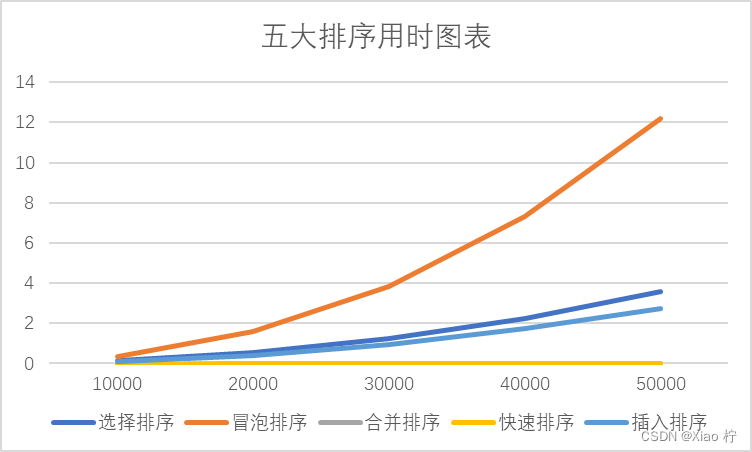
我们可以清晰的看出:
当数量级很小时,六种排序方式都比较省时间;当数量级在10^4左右时,其算法的时间消耗差距不大;但当数据量较大时,快速排序、合并排序有着十分明显的优势,插入排序和选择排序性能中规中矩,而冒泡排序则需要小号更多的时间去完成排序操作
对于数据量较少时,时间复杂度O(n^2)的算法和时间复杂度为O(nlogn)的算法区别不大,都能较好的完成排序,当数据量变大时,时间复杂度为O(nlogn)的算法便会体现出明显的优势,因此,当数据量较大时,我们应该优先采取快速排序,合并排序等算法
问题5
- 小规模数据测试
令输入的向量值为5,7,2,18,54,23,43,6,98,56,34,12,32,46,57,78,31,35,10,30共20个数,运行程序,可得到三种方法运行的结果如下:
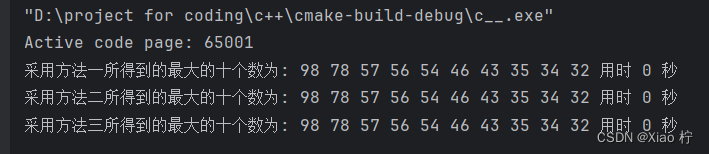
即满足查找最大的十个数,进一步验证了算法的正确性
- 大规模数据计算
将输入规模从1000000 至 10000000变化,同样进行20次测试,并取平均值,令k=10,可得到以下运行时间:
数据总览
| 数量级 | 1000000 | 2000000 | 4000000 | 8000000 | 10000000 |
| 方法一 | 0.2673 | 0.5566 | 1.1375 | 2.3171 | 2.92715 |
| 方法二 | 0.1763 | 0.33785 | 0.67795 | 1.3776 | 1.7324 |
| 方法三 | 0.0107 | 0.2125 | 0.04205 | 0.08275 | 0.10405 |
将数据可视化,做成图表如下所示:
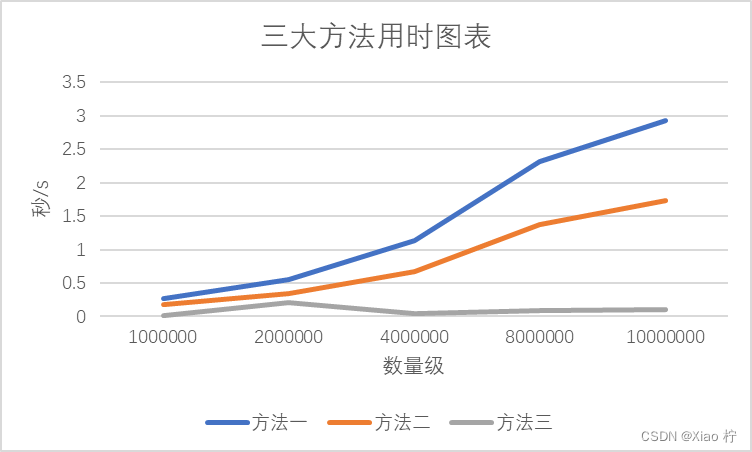
我们可以清晰的看出:
- 方法一排序方法的时间复杂度最高,为O(nlogn),查找的速度最慢
- 方法二比方法三的速度慢,其原因为方法三只需要进行一次遍历,而方法二需要进行k次遍历
- 方法二和方法三均为线性复杂度,但由于此题k值不变,均无法体现
继续对第三种方法进行规模测试,输入规模从100000000到1500000000 变化,从运行时间可以看出,依旧可以迅速得到最大的十个数:
| 数量级 | 100000000 | 500000000 | 800000000 | 100000000 | 1500000000 |
| 方法三 | 1.126 | 5.844 | 9.088 | 11.481 | 17.016 |
可见算法三对应用于大规模数据的正确性
七、实验结论
从算法解决问题的角度写你得到的结论是什么,注意不要写个人心得。
- 当调用相关函数时,若参数传递为引用传递或指针传递时,传输效率会明显高于直接传值,能够有效提高程序运行的效率
- 减少无效循环次数不能提升算法的效率
在冒泡排序中,我试图设置标志,若不在进行交换操作,则意味着序列已经有序,因此我设置了如下代码进行测试
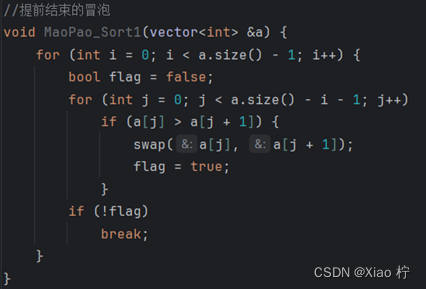
运行结果如表:
| 数量级 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 无优化 | 0.379 | 1.625 | 3.986 | 7.47 | 12.199 |
| 优化 | 0.383 | 1.667 | 4.158 | 7.716 | 12.244 |
可见,不但没有优化性能,还增加了运行时间!
在面对大规模数据需要处理时,我们要选择时间复杂度低的算法进行实验,并且在编写代码时也要尽力降低算法的时间复杂度



![[Qt的学习日常]--常用控件1](https://img-blog.csdnimg.cn/direct/11b2841c8d1c469d948e20f2d9089cfc.png)



![[C++ STL] vector 详解](https://img-blog.csdnimg.cn/direct/6810814cc5f64abca5ed579d5e778c38.png)