---

  Numpy是 Python 语言的一个扩展程序库，其中提供了许多向量和矩阵操作，底层用C语言编写，其对数组的操作速度不受python解释器的限制，处理速度快，效率远高于纯python代码。查看当前使用numpy的版本：

import numpy as np
print(np.version())	#1.26.4

一、数据维度的概念

  维度是数据的组织形式。

1.1常见的多维数据

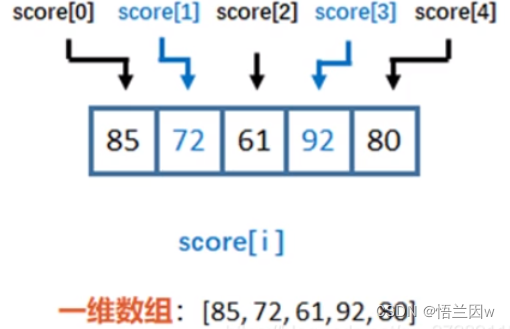
1.一维数据
  一维数据由对等关系的有序或无需数据构成，采用线性方式组织。常见的一维数据组织形式如列表（数据元素可不同，有序）、数组（数据元素相同、有序）、集合（数据元素可不同，无序）。一维数组使用一个下标即可确定一个元素。

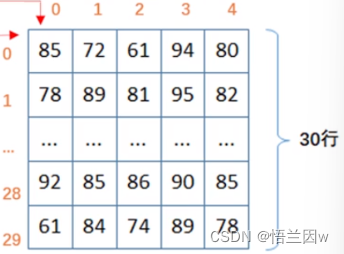
2.二维数据
  二维数据是一维数据的组合形式，常见的表格就是二维数据格式。二维数组使用两个下标确定一个元素，其中第一个下标表示一维数组，第二个下标表示数据在该一维数组中的位置

在numpy当中，使用一维数组的集合来表示二维数组：

print(np.array([[1,  2],  [3,  4]]) )

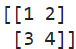
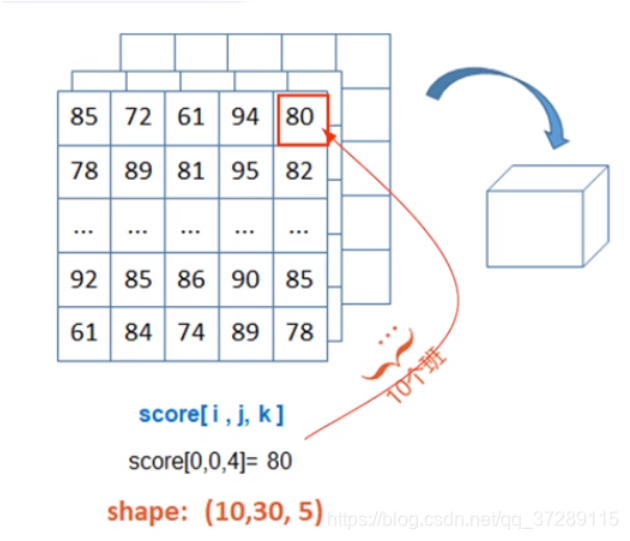
3.三维数据
  三维数据是二维数据的组合形式（在新维度上扩展形成），表现为一个数据立方体。三维数组使用三个下标确定一个元素，其中第一个下标确定二维数组、第二个下标确定二维数组中的一维数组、第三个下标确定元素的位置。

在numpy当中，使用二维数组的集合来表示三维数组：

print(np.array([[[1,  2],  [3,  4]],[[5,  6],  [7,  8]]]) )

1.2numpy的维度、形状、轴

1.2.1维度

  在机器学习、线性代数当中常见的m维行向量、n维列向量、mxn阶矩阵的概念如下：

• m维行向量：一个行向量中有m列数据。
• n维列向量：一个列向量中有n行数据。
• mxn阶矩阵：可看作是m个n维列向量，或是n个m维行向量组成。

但在numpy当中，维度（dimension）指的是坐标系的维度，如一维指只有x轴、二维指xoy坐标系、三维指xoyz坐标系，由于不同坐标系所含轴数不同，所以numpy中维度也可指数组轴（axis）的数目，并且可以使用.ndim获取数组的轴数（维度数）：

# 创建零维数组(标量)
arr0=np.array(1)
# 创建一维数组
arr1=np.array([1,2,3,4])
# 创建二维数组
arr2=np.array([[1,2,3],[4,5,6]])
# 创建三维数组
arr3=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print(f'零维数组的轴数为{arr0.ndim},一维数组的轴数为{arr1.ndim},二维数组的轴数为{arr2.ndim},三维数组的轴数为{arr3.ndim}')

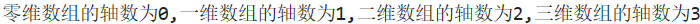
事实上，也可通过数组包含方括号的个数来判断数组的维度，如[[[...]]]是三维，而[[[[[[......]]]]]]是六维。

注意，[1]与1是不同的概念，前者表示只含有一个元素的一维数组，其轴为1，而后者表示标量，轴为零。

1.2.2形状

  数组形状描述了这个数组的样式，即有多少行、多少列以及在更高维度中如何组织数据。numpy中的数组提供了属性shape来返回一个用于表示数组形状的元组，如：

arr=np.array([[[1,2],[3,4]],[[5,6],[7,8]],[[9,10],[11,12]]])
print(f'数组的形状是{arr.shape}')

即三维数组中包含了3个二维数组，每个二维数组都包含2个一维数组，每个一维数组都包含了两个元素。事实上，从属性返回的元组也可看出数组的维度：

• ()：表示零维。
• (5,)：表示一维。注意区分元组中(5)和(5,)。
• (2,3)：表示二维。
• (2,3,4)：表示三维。

1.2.3轴

  前文提到，numpy中的轴（axis）与坐标系轴的概念类似且有着自己的方向。事实上，numpy使用axis 序号作为轴的名称，从0开始计数，数组维度与axis的取值关系如下：

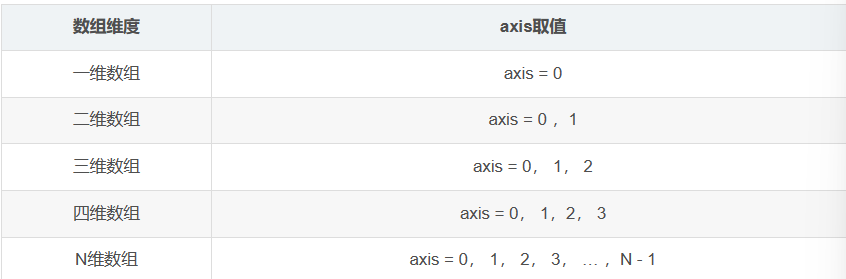
注意，axis=0每次表示的都是新增轴。
1.一维数组的轴

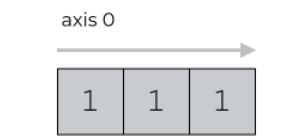
  一维数组只包含axis=0轴，代表数组的列变换：

arr=np.array([1,2,3])
print(arr)
print(arr.shape)

其中，axis=0对应shape属性中的3，表示该轴方向上共有三组元素可供操作。

2.二维数组的轴

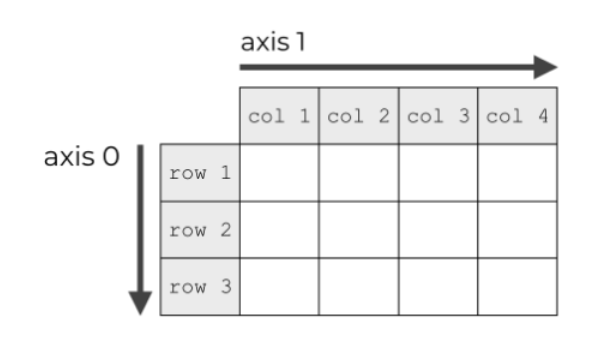
  在二维数组中，使用axis=0（0轴）表示新增的横轴（横并不是axis的指向），代表行变换，用axis=1表示竖轴，代表列变换。并且，每个轴都对应shape属性中的一个元素，如：

其中，axis=0对应3，表示共有三行（三个一维数组）元素，axis=1对应4，表示共有四列（每个一维数组有四个）元素。

3.三维数组的轴

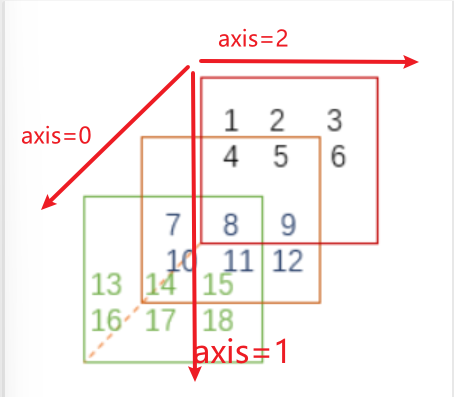
arr=np.arange(1,19).reshape(3,2,3)
print(arr)

• axis=0：表示新增轴，此处可理解为深度，对应arr.shape[0]，表示包含两个三维数组。
• axis=1：表示横轴，对应arr.shape[1]，表示每个二维数组包含两个一维数组。
• axis=2：表示数轴，对应arr.shape[2]，表示每个一维数组含有3个元素。

1.3reshape()函数

  np.reshape()函数是numpy 中用于改变数组形状的函数，注意，传入数组大小的乘积（一般使用元组表示）必须等于数组中元素的个数。例：

array  = np.array([1,2,3,4,5,6,7,8,9,10,11,12])
array.reshape(2,2,3)

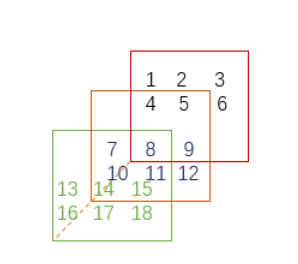
即，数组共有12个元素，而2*2*3=12.

1.4numpy中行、列向量的表示

  在numpy中创建42的数组a与21的矩阵b，并对二者使用点乘操作np.dot()：

# 创建4*2数组
a = np.array([[1,1,1,1],[1,1,1,1]]).T
# 创建一维数组b
b = np.array([2,3]) 
# 点乘操作a·b
print('a·b=',np.dot(a,b))# 将b数组转置
b = b.T
# 点乘操作a·b
print('a·b=',np.dot(a,b))

• 若b表示2维行向量：42矩阵与12矩阵相乘应报错，但没有。
• 若b表示2维列向量：42矩阵与21矩阵相乘应报错，但没有。

即，一维数组b既可表示行向量，也可表示列向量。并有以下结论

• numpy中的一维数组可同时表示行、列向量，这取决于和它进行点乘的矩阵是什么。
• 在习惯上为避免不确定是行还是列向量，可使用二维数组表示行列向量。如：

a = np.array([[2,3]]) #行向量
b = np.array([[2],[3]]) #列向量
print(a.shape)
print(b.shape)

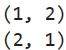
1.5数组的迭代

  NumPy包含一个迭代器对象numpy.nditer，可以用于在数组上进行迭代。

a = np.array([[1,2,3],[4,5,6]])
for x in np.nditer(a):print(x)

1.6添加/删除元素

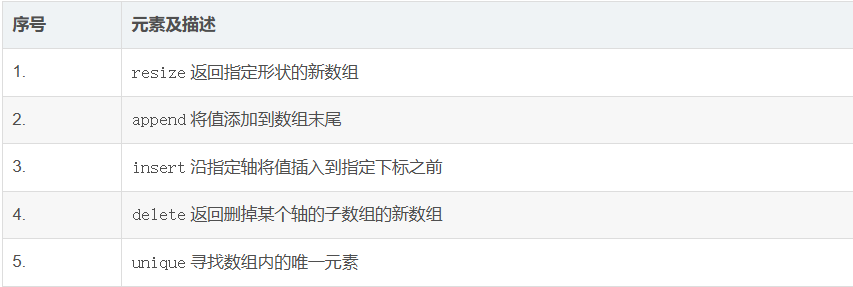
1.6.1append()

  此函数用于在输入数组的末尾添加值：

numpy.append(arr, values, axis)

• arr：输入数组。
• values：要向arr添加的值，比如和arr形状相同（除了要添加的轴）。
• axis：沿着它完成操作的轴。如果没有提供，两个参数都会被展开。

 import numpy as np 
a = np.array([[1,2,3],[4,5,6]]) print('原始数组：')
print(a)
print('\n')  print('向数组添加元素：')
print(np.append(a, [7,8,9])) 
print('\n')print('沿轴 0 添加元素：')
print(np.append(a, [[7,8,9]],axis = 0))
print('\n')print('沿轴 1 添加元素：')
print(np.append(a, [[5,5,5],[7,8,9]],axis = 1))

1.6.2insert()

  此函数用于向数组中插入元素：

 numpy.insert(arr, obj, values, axis)

• arr：输入数组。
• obj：在其之前插入值的索引。
• values：要插入的值。
• axis：沿着它插入的轴，如果未提供，则输入数组会被展开。

a = np.array([[1,2],[3,4],[5,6]]) print('第一个数组：')
print(a)print('未传递 Axis 参数。 在插入之前输入数组会被展开。')
print(np.insert(a,3,[11,12]))
print('\n')
print('传递了 Axis 参数。 会广播值数组来配输入数组。')print('沿轴 0 插入：')
print(np.insert(a,1,[11],axis = 0))
print('\n')print('沿轴 1 插入：') 
print(np.insert(a,1,11,axis = 1))

1.6.3delete()

  此函数返回从输入数组中删除指定子数组的新数组。 与insert()函数的情况一样，如果未提供轴参数，则输入数组将展开。 该函数接受以下参数：

Numpy.delete(arr, obj, axis)

import numpy as np 
a = np.arange(12).reshape(3,4) print('第一个数组：')
print(a)
print('\n')print('未传递 Axis 参数。 在插入之前输入数组会被展开。')
print(np.delete(a,5))
print('\n')print('删除第二列：')  
print(np.delete(a,1,axis = 1))
print('\n')print('包含从数组中删除的替代值的切片：')
a = np.array([1,2,3,4,5,6,7,8,9,10])
print(np.delete(a, np.s_[::2]))

二、Ndarray对象

2.1简介

  NumPy 中定义的最重要的对象是称为 ndarray 的 N 维数组类型。 它描述相同类型的元素集合，可以使用基于零的索引访问集合中的元素。由于数据类型确定，ndarray中的每个元素在内存中使用相同大小的块。事实上，ndarray由实际的数据、描述这些数据的元数据（数据维度、数据类型等信息）两部分构成，打印输出时，使用[]表示。

2.1.1常用属性

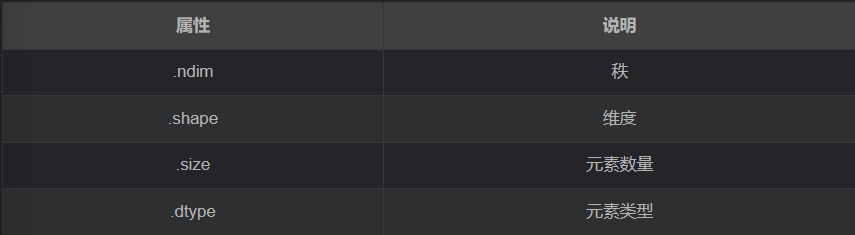
arr=np.array([[1,2,3],[4,5,6]])
print(f'arr.ndim={arr.ndim}\narr.shape={arr.shape}\naarr.size={arr.size}\narr.dtype={arr.dtype}')

2.1.2.ndarray对象的数据类型

类型	类型代码	说明
int8/16/32/64	i1/i2/i4/i8 （数字表示字节数）	有符号8/16/32/64位整数
uint8/16/32/64	u1/u2/u4/u8 （数字表示字节数）	无有符号8/16/32/64位整数
float16/32/64/128	f2/f4/f8/f16（数字表示字节数）	半精度浮点数、标准的单精度浮点数（与C语言float兼容）、标准的双精度浮点数（与C语言的double、Python的float对象兼容）、扩展精度浮点数
complex64/128/256	c8/c16/c32	分别用两个32位，64位，128位浮点数表示的复数（含实部与虚部）
bool	?	存储True和False值的布尔类型
object	O	python对象类型
String	S	固定长度的字符串类型(每个字符一个字节)。例如：要创建一个长度为10的字符串，应使用S10
unicode_	U	固定长度的Unicode类型(字节数由平台决定)跟字符串的定义方式一样

np.array(range(10),dtype='f') 

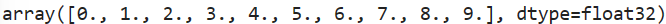
2.2创建ndarray对象

2.2.1array()

  array()是最基本的ndarray对象创建函数，接收一切序列型的对象，比如：列表、元组、可迭代对象等，也包括它自己。

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

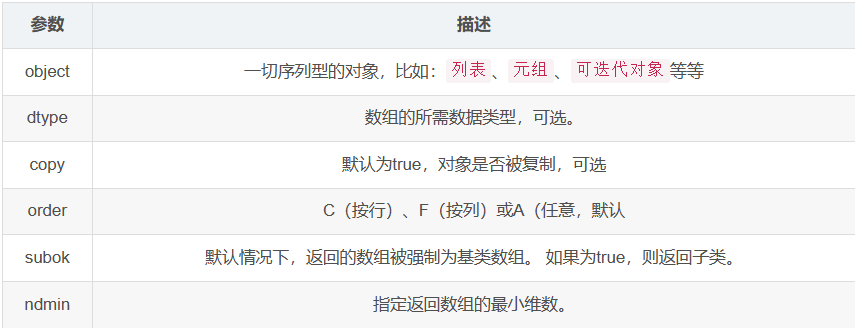
当不指定dtype时，numpy将根据实际情况创建：

# 1.当不指定dtype时，NumPy将根据数据情况关联一个dtype类型
array = np.array([[1,2,3],[4,5,6]])
print(array.dtype) # int32# 2.指定dtype进行创建
np.array([1,2+2.5j,3.1-5j],dtype=complex) # [1. +0.j  2. +2.5j 3.1-5.j ]# 3.使用序列创建
arr1=np.array([0,1,2,3]) # 使用列表创建
arr2=np.array((0,1,2,3)) # 使用元组创建
arr3=np.array([[1,2],[3,4],(0.1,0.2)]) # 列表+元组创建

2.2.2arange()

  arange()可用于创建指定数据范围的ndarray对象。

numpy.arange(start, stop, step, dtype)

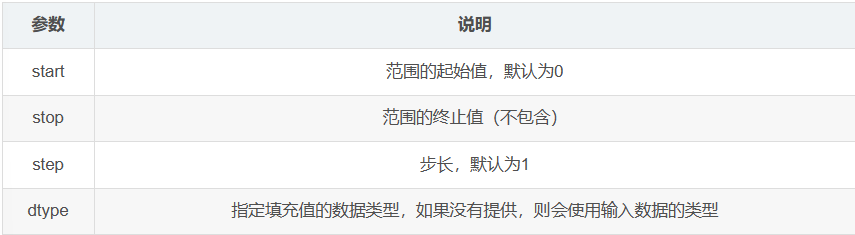
np.arange(5, dtype=float) # [0. 1. 2. 3. 4.]

2.2.3empty()

  empty()返回一个新的未初始化的数组，这意味着新数组的内容是未定义的，它包含了数组创建时存在于内存中的任意数据。

np.empty((3,3,2))

2.2.5ones()、zeros()、full()

  ones()、zeros()用于返回用1、0填充的ndarray对象：

numpy.ones(shape, dtype = None, order = 'C')
numpy.zeros(shape, dtype = None, order = 'C')

np.zeros(5)  # 默认类型为float64

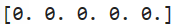
  full()用于返回一个使用指定值填充的ndarray对象：

np.full(shape, fill_value, dtype=None, order='C')

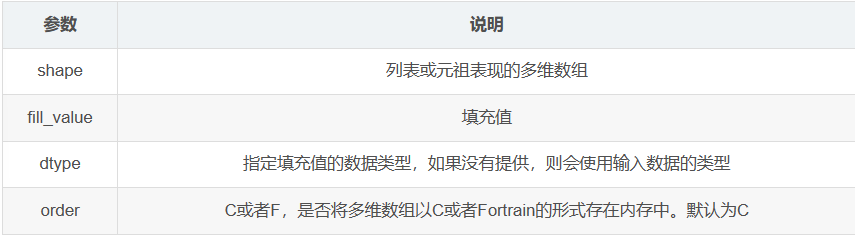
np.full((2, 2), np.inf)

2.2.6eye()

  eye()用于返回一个使用指定值填充的对角方阵。

np.eye(N, M=None, k=0, dtype=float, order='C')

a = np.eye(5, k=-2)
b = np.eye(5, k=2)
c = np.eye(5)
print(a) # 右移两格
print(b) # 左移两格
print(c) # 对角方阵

2.2.7repeat()

  将输入值的整体或某部分，在原来的基础上，进行指定次数的复制，从而创建新的输出值。

np.repeat(a, repeats, axis=None)

x=np.array([[1,2],[3,4]])
# 沿axis=0方向分别复制一次、两次
np.repeat(x,[1,2],axis=0)

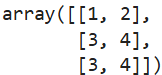
2.2.8linspace()

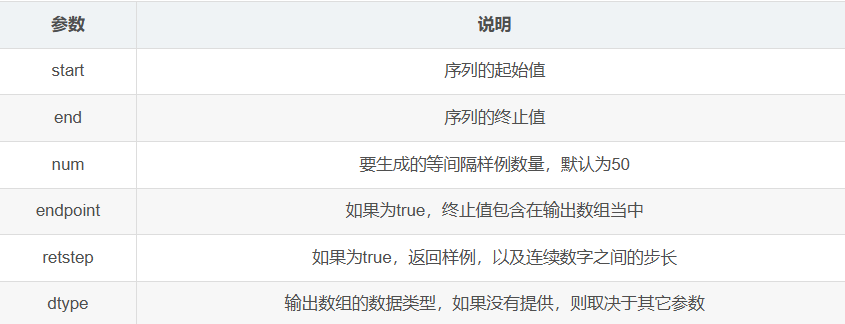
  linspace()用于创建指定范围的等差数组，

numpy.linspace(start, stop, num, endpoint, retstep, dtype)

# 生成10~20含有5个数的等差数列
np.linspace(10,20,5)

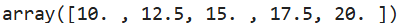
2.2.9logspace()

numpy.logscale(start, stop, num, endpoint, base, dtype)

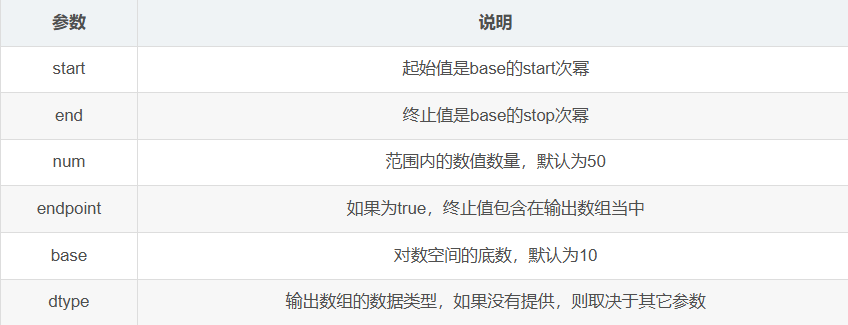
#生成100~1000含有50个数的等比数列
np.logspace(2,3,50)

2.2.10asarray()

  asarray()用于将输入的python序列转化为ndarray对象，类似于array()：

numpy.asarray(a, dtype = None, order = None)

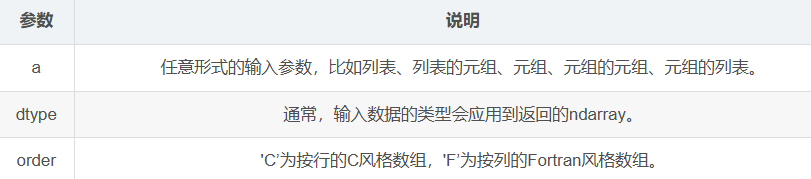
list1 = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]
np.asarray(list1)

三、Ndarray维度变换

  numpy提供以下函数对ndarray数组进行维度变换变换：

3.1reshape()

reshape(a, newshape, order='C')

#1.reshape,返回新数组，不会改变原数组
arr=np.array([[1,2,3],[4,5,6]])
b=arr.reshape(3,2)
print('arr=',arr)
print('b=',b)

3.2resize()

resize(a, new_shape)

#2.resize,直接在原数组上进行修改,无返回值
arr=np.array([[1,2,3],[4,5,6]])
arr.resize(3,2)
print(arr)

3.3swapaxes()

swapaxes(a, axis1, axis2)

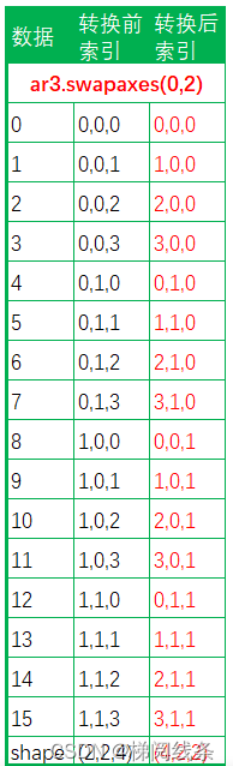
• a：要进行轴交换的数组。
• axis1：要交换的第一个轴的索引。
• axis2：要交换的第二个轴的索引。

  因为ndarray.swapaxes()需要2个轴作为入参，所以，一维数组不可调用swapaxes()。在使用ndarray.swapaxes()后，访问元素所用的索引发生了调换：

3.4flatten()

  对数组进行降维，返回一维数组，原数组保持不变，属于深拷贝（新数组被分配了新的地址，所以改变自身的值，原值不受影响）：

a = np.arange(12).reshape(2, 3, 2)
b=a.flatten()
b[0]=20
print(a)
print(b)

由于是深拷贝，当b的值进行修改时，a数组中对应的值并未改变。

3.5ravel()

  对数组进行降维，返回一维数组，原数组发生改变，属于浅拷贝（返回新对象的指针仍指向原数组）：

a = np.arange(12).reshape(2, 3, 2)
b=a.ravel()
b[0]=20
print(a)
print(b)

由于是浅拷贝，当b的值进行修改时，a数组中对应的值发生改变。

四、类型变换、拼接、分割

4.1astype()

  astype()函数可用于array中数值类型的转换。

arr = np.arange((10))
print(arr, arr.dtype, sep="\n")
arr = arr.astype("float32")
print(arr, arr.dtype, sep="\n")

4.2tolist()

  numpy中提供了dnarray向list类型转换的函数，若直接使用list()，则无法完全进行转换：

arr=np.array([[1,2,3],[4,5,6]])
list(arr)

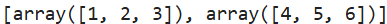
arr=np.array([[1,2,3],[4,5,6]])
arr.tolist()

4.3T()

  numpy对二维数组提供了转置操作：

arr=np.array([[1,2,3],[4,5,6]])
arr.T

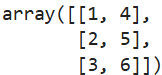
4.4vstack()：垂直堆叠

numpy.vstack(tup)

  vstack()函数用于在垂直方向上堆叠数组，即将多个数组按行方向堆叠，其中，tup是包含了要堆叠数组的元组，这些数组必须有相同的列数。

#一维数组
a = np.array([1,2,3])
b = np.array([4,5,6])
print(np.vstack((a,b)) )
#二维数组
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
print(np.vstack((a,b)))
#三维数组
a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
b = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(np.vstack((a,b)))

4.5hstack()：水平堆叠

  hstack()表示进行水平堆叠，实质是按axis=1将每个垂直的列都堆叠在一起，则要求行数相等：

#一维数组
a = np.array([1,2,3])
b = np.array([4,5,6])
print(np.hstack((a,b)) )
#二维数组
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
print(np.hstack((a,b)))
#三维数组
a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
b = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(np.hstack((a,b)))

4.7stack()：自定义堆叠

np.stack(arrays, axis=0, out=None)

a = np.arange(0,2)
b = np.arange(2,4)
c = np.arange(4,6)
'''
[0, 1]
[2, 3]
[4, 5] ->
沿着axis=0堆叠：
[[0, 1],
[2, 3],
[4, 5],]
'''a = np.arange(0,2)
b = np.arange(2,4)
c = np.arange(4,6)
'''
[0, 1]
[2, 3]
[4, 5] ->
沿着axis=1拼接：
[[0,2,4],
[1,3,5]]
'''
np.stack((a,b,c), axis=1)

4.8concatenate()：自定义拼接

numpy.concatenate((a1, a2, ...), axis=0, out=None)

  concatenate()函数用于沿指定轴将多个数组合并成一个新的数组。

• (a1, a2, ...)：要合并的数组序列，以元组形式传入。
• axis：指定合并的轴，即沿着哪个维度进行合并。默认值为 0，表示沿着第一个维度进行合并。
• out：指定输出数组的可选参数。

1.合并一维数组

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
np.concatenate((a,b))

2.合并二维数组

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
print(np.concatenate((a,b)))
print(np.concatenate((a,b),axis=1))

4.9split()

  split()函数用于将一个数组拆分为多个子数组，返回的是多个数组。

split(ary, indices_or_sections, axis=0)

• ary：待分割的原始数组。
• indices_or_sections：int或者一维数组，表示一个索引，也就是切的位置所在。
  • int：用这个数平均分割原数组。
  • 一维数组：以数组中的数字为索引切开。
• axis：选定切的维度。

x = np.array([1,2,3,4,5,6,7,8,9])
# 平均切分为3个数组
print(np.split(x, 3))A = np.arange(36).reshape((2, 2, 9)) 
#表示按axis=2，即(2,2,9)中的9处切分，切分为[0:2]、[3:5]、[6:8]3个数组
[A1, A2, A3] = np.split(A, [3, 6], axis=2)
print(A1, A2, A3,sep='\n')

五、索引与切片

  nadarry数组的操作包括数组的索引和切片。

• ①索引：获取数组中特定位置元素的过程。
• ②切片：获取数组元素子集的过程。

5.1切片

一维数组的切片

a = np.array([9,8,7,6,5])
print(a[2])	# 7
print(a[1:4:2]) #起始编号：终止编号(不含)：步长
# [8 6]

二维数组的切片

a = np.array([[0, 1, 2], [4, 5, 6]])
print(a[0])
# [0 1 2]
print(a[0:2])
"""
[[0 1 2][4 5 6]]
"""
print(a[:2])
"""
[[0 1 2][4 5 6]]
"""
print(a[0:2, 0:2])
"""
[[0 1][4 5]]
"""
print(a[0:2, 1:3])
"""
[[1 2][5 6]]
"""
print(a[:, 0])
"""
[0 4]
"""

三维数组的切片

a = np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]])
print(a[:, :, 0])
"""
[[0 3][6 9]]
"""
print(a[:, :, 0:2:2]) # print(a[:, :, ::2])
"""
[[ 2  5][ 8 11]]
"""

  切片还可以包括省略号（…），来使选择元组的长度与数组的维度相同。 如果在行位置使用省略号，它将返回包含行中元素的数组。

a = np.array([[1, 2, 3], [3, 4, 5], [4, 5, 6]])
print(a)
"""
[[1 2 3][3 4 5][4 5 6]]
"""
# 这会返回第二列元素的数组：
print(a[..., 1])
"""
[2 4 5]
"""
# 现在我们从第二行切片所有元素：
print(a[1, ...])
"""
[3 4 5]
"""
# 现在我们从第二列向后切片所有元素：
print(a[..., 1:])
"""
[[2 3][4 5][5 6]]
"""

5.2索引

a = np.arange(24).reshape((2, 3, 4))
print(a)
print(a[1, 2, 3])  #每个维度一个索引值，逗号分割
print(a[-1, 2, -2])
"""
[[[ 0  1  2  3][ 4  5  6  7][ 8  9 10 11]][[12 13 14 15][16 17 18 19][20 21 22 23]]]
"""
"""
23
22
"""

布尔索引：使用布尔数组作为索引。arr[condition]，condition为一个条件/多个条件组成的布尔数组。

x = np.array([3, 2, 3, 1, 3, 0])
# 布尔型数组的长度必须跟被索引的轴长度一致
y = np.array([True, False, True, False, True, False])
print(x[y])  # [3,3,3]
print(x[y == False])  # [2,1,0]
print(x >= 3)  # [ True False  True False  True  False]
print(x[~(x >= 3)])  # [2,1,0]
print((x == 2) | (x == 1))  # [False  True False  True False False]
print(x[(x == 2) | (x == 1)])  # [2 1]
x[(x == 2) | (x == 1)] = 0
print(x)  # [3 0 3 0 3 0]

六、广播

6.1简介

  对数组的算术运算通常在两个具有完全相同形状的阵列之间进行，如：

a = np.array([1,2,3,4]) 
b = np.array([10,20,30,40]) 
a*b

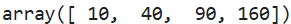
此时两个数组相应的元素之间进行计算。而若两个数组的维数不相同，由于numpy具有广播的性质，使得计算仍可继续进行。例如：

a = np.array([1, 2, 3])
print(a*2)

严格意义上，数组a大小为(1,3)，而2属于标量，二者并不能直接进行计算。而numpy的广播机制对标量2进行了扩容，使得计算可正常进行：

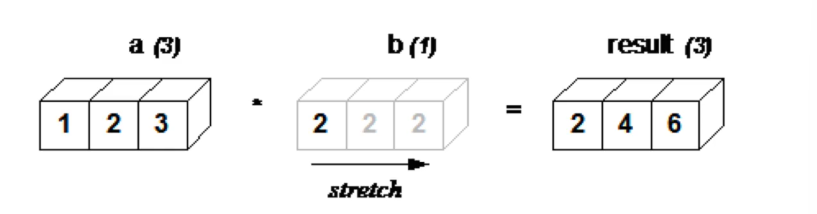
再比如以下计算仍可正常进行：

a = np.array([[0, 0, 0],[10, 10, 10],[20, 20, 20],[30, 30, 30]])
b = np.array([1, 2, 3])
print(a+b)

6.2广播规则

  当对两个 array 进行操作时，numpy 会从最大的axis（shape属性最右侧的值）开始向左进行比较，只有：

• 1.两维度相等。
• 2.两维度其中一个为1。

此时，两维度才会被认为是兼容的，否则抛出异常显示无法计算。例如一个形状为256 x 256 x 3的三维数组与大小为(3,)的一维数组进行计算：

三维数组形状：256 x 256 x 3
一维数组形状：            3	， 会被拉伸为1 x 1 x 3
结果的形状：  256 x 256 x 3

当比较的任一维度大小是 1 时，使用另一个数组对应维度的大小。同理：

A      (4d array):  8 x 1 x 6 x 1
B      (3d array):      7 x 1 x 5
result (4d array):  8 x 7 x 6 x 5

而以下例子中，倒数第二个维度不满足上述条件，故无法计算：

A      (2d array):      2 x 1
B      (3d array):  8 x 4 x 3 # 倒数第二个维度不兼容

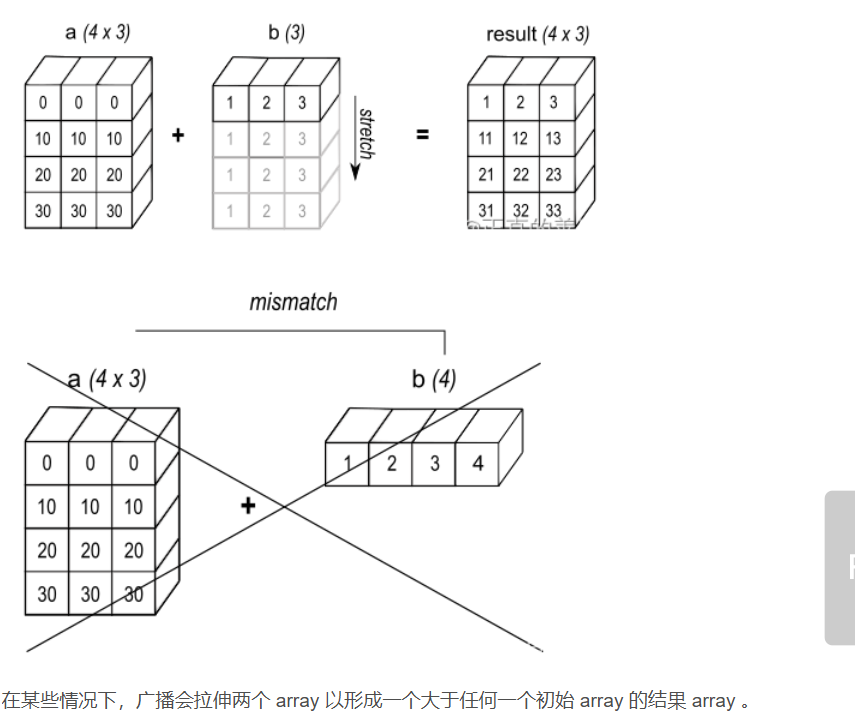
  以图为例：

>>> a = np.array([[ 0.0,  0.0,  0.0],
...               [10.0, 10.0, 10.0],
...               [20.0, 20.0, 20.0],
...               [30.0, 30.0, 30.0]])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a + b
array([[  1.,   2.,   3.],[11.,  12.,  13.],[21.,  22.,  23.],[31.,  32.,  33.]])
>>> b = np.array([1.0, 2.0, 3.0, 4.0])
>>> a + b
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (4,3) (4,)

七、其他操作

7.1axis作为函数参数时的技巧

  axis常常作为函数参数进行使用，但在实际使用过程当中自行判断操作的元素非常麻烦，此处参考文章：文章链接。此方法包含两步思路：

• 由axis=value找到对应[]中的最大单位块
• 对最大单位块进行操作。
  • 当单位块是数值时直接计算。
  • 当单位块是数组时，将对应下标元素进行计算。

7.1.1思路解析

寻找最大单位快：某层[]里包裹的最大结构块。

• [1,2,3]：数值1，2，3，axis取值为0.
• [[1,2],[3,4]：[1,2]，[3,4]，axis取值为0、1.
• [[[1,2],[3,4]],[[5,6],[7,8]]]：[[1,2],[3,4]]、[[5,6],[7,8]]，axis取值为0、1、2.

对单位块进行操作：最大单位块是数值时直接计算即可，而当其是数组时，如[[[1,2],[3,4]],[[5,6],[7,8]]]，axis=0对应三维数组最外层，即其中包含[[1, 2],[3, 4]]、 [[5, 6],[7, 8]]两个最大单位块。而axis=1对应第二层，其中包含两组元素，每组包含两个单位最大块，即[1,2]和[3,4]、[5,6]和[7,8]。同理，axis=2对应的最大块都是数值，直接计算即可。

7.1.2实例1：sum函数

一维数组
  一维数组维度为1，只有axis=0时的情形：

arr = np.array([1, 2, 3])
arr.sum(axis = 0)	# 6

• axis=0对应最外层[]，单位最大块为数值1，2，3。
• 直接对数值求和计算。

二维数组
  二维数组维度为2，有axis=0、axis=1时的情形：
axis=0：

arr = np.array([[1, 2], [3, 4]])
arr.sum(axis = 0)	# array([4, 6])

• axis=0对应最外层[]，包含[1,2]和[3,4]两个最大单位块。
• 单位块是数组，则二者对应下标元素进行计算，即[1,2]中1对应下标0，2对应下标1，同样[3,4]中3对应下标0，4对应下标1，则有[1+3，2+4]=[4，6]。

axis=1：

rr = np.array([[1, 2], [3, 4]])
arr.sum(axis = 1)	# array([3, 7])

• axis=1对应第二层[]，在第一个[]中包含1，2（数值形式的最大单位块），第二个[]中包含3，4.
• 单位块是数值，直接进行计算，即[1+2，3+4]=[3，7]。

三维数组
  二维数组维度为3，有axis=0、axis=1、axis=2时的情形：
axis=0

arr = np.array([[[1, 2],[3, 4]], [[5, 6],[7, 8]]])
arr.sum(axis=0)	# array([[ 6,  8],[10, 12]])

• axis=0对应最外层[]，包含最大单位块为[[1, 2],[3, 4]]与[[5, 6],[7, 8]]。
• 由于单位块是数组，则将对应下标元素进行计算，即[[1, 2]，[3, 4]] + [[5, 6],[7, 8]] = [[1+5，2+6]，[3+7，4+8]] = [[6，8]， [10，12]]。

axis=1

arr = np.array([[[1, 2],[3, 4]], [[5, 6],[7, 8]]])
arr.sum(axis=1)	# array([[ 4,  6],[12, 14]])

• axis=1对应第二层[]，注意，去掉第一层[]时获得两个最大单位块[[1, 2],[3, 4]]和[[5, 6],[7, 8]]（即两个数组），则去掉第二层[]时同样获得两组（每组两个）最大单位块，第一组中为[1, 2]和[3, 4]]，第二组中为[5, 6]和[7, 8]。
• 由于对应最大单位块是数组，故将两组单位块对应元素进行计算，即[[1+3，2+4]，[5+7， 6+8]] = [[4，6]，[12，14]]。

axis=2

arr = np.array([[[1, 2],[3, 4]], [[5, 6],[7, 8]]])
arr.sum(axis=2)	# array([[ 3,  7],[11, 15]])

• axis=2对应第三层[]，去掉第二层[]时获得两组最大单位块，第一组中为[1, 2]和[3, 4]，第二组中为[5, 6]和[7, 8]，即四个数组。故去掉[]获得数值形式的最大单位块，第一组为1和2，第二组为3和4，第三组为5和6，第四组为7和8，注意1，2，3，4同属第一层中的一组，5，6，7，8属另一组（注意，即使不存在[]，也不可随意合并分组）。
• 由于最大单位块是数值，故将同属一个单位块的数据进行运算，即[[1+2，3+4]，[5+6，7+8]] = [[3，7]，[11，15]]。

axis=-1：表示在当前数组最后一维度操作，三维数组中axis=0/1/2，那么axis=-1即等价于axis=2，所以其结果与axis=2相同。

7.1.3实例2：argmax函数

  argmax函数用于获取数组中元素最大值的下标。
一维数组

arr = np.array([3, 4, 6, 9, 1, 2])
print(np.argmax(arr, axis=0))	# 3

二维数组
axis=0

arr = np.array([[3, 6, 6, 2], [4, 7, 11, 2], [5, 9, 1, 3]])
print(np.argmax(arr, axis=0))	# [2 2 1 2]

• axis=0对应最外层[]，去掉[]后得到三个最大单位块[3, 6, 6, 2]，[4, 7, 11, 2]，[5, 9, 1, 3]。
• 单位块是数组，则对应下标元素进行计算，即argmax([3，4，5])、argmax([6，7，9])、argmax([6，11，1])、argmax([2，2，3])，得到4个最大值索引值：2、2、1、2，得到索引值数组：[2 2 1 2]。

axis=1

arr = np.array([[3, 6, 6, 2], [4, 7, 11, 2], [5, 9, 1, 3]])
print(np.argmax(arr, axis=1))	# [1 2 1]       

• axis=0对应[]去掉后得到[3, 6, 6, 2]，[4, 7, 11, 2]，[5, 9, 1, 3]，将axis=1对应[]去掉后得到三组元素3, 6, 6, 2、4, 7, 11, 2和5, 9, 1, 3。
• 由于单位块是数值形式，故直接进行计算，即argmax([3，6，6，2])、argmax([4，7，11，2])、argmax([5，9，1，3])，得到3个最大值索引值：1、2、1，得到索引数组：[1 2 1]。

三维数组
axis=0

arr = np.array([[[1, 5, 5, 2], [9, -6, 2, 8], [-3, 7, -9, 1]], [[-1, 7, -5, 2], [9, 6, 2, 8], [3, 7, 9, 1]], [[21, 6, -5, 2], [9, 36, 2, 8], [2, 7, 66, 1]]])
print(np.argmax(arr, axis=0))
'''
[[2 1 0 0][0 2 0 0][1 0 2 0]]'''

• axis对应最外层[]，去掉后得到：[[1, 5, 5, 2], [9, -6, 2, 8], [-3, 7, -9, 1]]、[[-1, 7, -5, 2], [9, 6, 2, 8], [3, 7, 9, 1]]、[[21, 6, -5, 2], [9, 36, 2, 8], [2, 7, 66, 1]]三个最大单位块。
• 由于最大单位块是数组，故将三者对应下标的元素进行计算：

即：argmax([1，-1，21)、argmax([5，7，6])、argmax([5，-5，-5])、argmax([2，2，2])、argmax([9，9，9])、argmax([-6，6，36])…以此类推，得到索引值数组：

axis=1

>>> arr
array([[[ 1,  5,  5,  2],[ 9, -6,  2,  8],[-3,  7, -9,  1]],[[-1,  7, -5,  2],[ 9,  6,  2,  8],[ 3,  7,  9,  1]],[[21,  6, -5,  2],[ 9, 36,  2,  8],[ 2,  7, 66,  1]]])
>>> print(np.argmax(arr, axis=1))
[[1 2 0 1][1 0 2 1][0 1 2 1]]

• 脱去两层[]后得到三组最大单位块，第一组中为[ 1, 5, 5, 2],[ 9, -6, 2, 8],[-3, 7, -9, 1]，第二组中为[-1, 7, -5, 2],[ 9, 6, 2, 8],[ 3, 7, 9, 1]，第三组中为[21, 6, -5, 2],[ 9, 36, 2, 8],[ 2, 7, 66, 1]。
• 将三组单位块中数组对应下标元素进行计算，如对于第一组的[ 1, 5, 5, 2],[ 9, -6, 2, 8],[-3, 7, -9, 1]有：

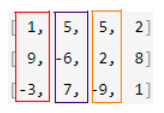
以此类推计算argmax([1，9，-3)、argmax([5，-6，7])、argmax([5，2，-9])、argmax(2，8，1)，得到索引数组：

axis=2

>>> arr
array([[[ 1,  5,  5,  2],[ 9, -6,  2,  8],[-3,  7, -9,  1]],[[-1,  7, -5,  2],[ 9,  6,  2,  8],[ 3,  7,  9,  1]],[[21,  6, -5,  2],[ 9, 36,  2,  8],[ 2,  7, 66,  1]]])
>>> print(np.argmax(arr, axis=2))
[[1 0 1][1 0 2][0 1 2]]

• 第二层[]对应[ 1, 5, 5, 2],[ 9, -6, 2, 8],[-3, 7, -9, 1]、[-1, 7, -5, 2],[ 9, 6, 2, 8],[ 3, 7, 9, 1]、[21, 6, -5, 2],[ 9, 36, 2, 8],[ 2, 7, 66, 1]三组单位最大块，将[]去掉后得到三组数值1，5，5，2和9，-6，2，8和-3，7，-9，1、-1，7，-5，2和9，6，2，8和3，7，9，1、21，6，-5，2和9，36，2，8和2，7，66，1。（注意，即使不存在[]，也不可随意合并分组）
• 直接在数值中进行计算argmax([1，5，5，2])、argmax([9，-6，2，8])、argmax([-3，7，-9，1])…

axis=-1，表示在当前数组最后一维度操作，三维数组中axis=0/1/2，那么axis=-1即等价于axis=2，所以其结果与axis=2相同。