幅值修正与能量修正过程(更正)
参考什么是泄漏?
参考什么是窗函数?
参考使用python实现快速傅里叶变换(FFT)
参考频谱泄露和窗函数以及加窗后幅度修正和python代码实现
1 快速傅里叶变换(FFT)
离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心,通过它把信号从时间域变换到频率域,进而研究信号的频谱结构和变化规律。但是它的致命缺点是:计算量太大,时间复杂度太高,当采样点数太高的时候,计算缓慢,由此出现了DFT的快速实现,即下面的快速傅里叶变换FFT。
快速傅里叶变换(FFT),计算量更小的离散傅里叶的一种实现方法。
1.1 原始信号
考虑一个有效值为1V,频率为20Hz的正弦波,如图1所示。
振幅A=np.sqrt(2)=1.414
正弦信号基础知识
y = A * sin(wt + b)
其中y是正弦信号
A是正弦信号的振幅
wt+b 为正弦信号的相位
w为角频率
频率f = w/2pi, w= 2pi*f
Fs = 1000 # 采样频率
f = 20 # 信号频率
A = np.sqrt(2) # 振幅,对应有效值为1V
t = np.linspace(0, 1, Fs) # 生成 1s 的时间序列
y = A * np.sin(2 * np.pi * f * t) # 给定信号
import matplotlib.pyplot as plt
plt.title('original data')
plt.plot(t, y)
plt.xlabel('time/s')
plt.ylabel('Amplitude/V')
plt.show()
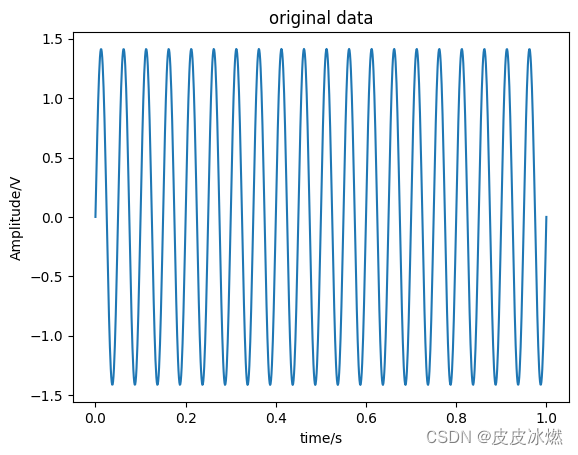
相当于知道采样频率Fs,一段时长为1s的信号,根据fft得到信号的频率。
1.2 scipy.fftpack.fft
快速傅里叶变换
scipy.fftpack.fft(x, n=None, axis=-1, overwrite_x=False)
其中n: 整数,可选,傅里叶变换的长度。如果n < x.shape[axis],x被截断。如果n > x.shape[axis],x是零填充的。默认结果是n = x.shape[axis]。
from scipy.fftpack import fft
fft_y=fft(y) #快速傅里叶变换
print(len(fft_y)) # 与原始信号相同长度
print(fft_y[:2]) # [6.19504448e-14-0.j 2.22183652e-04-0.07072302j]
发现以下几个特点:
(1)变换之后的结果数据长度和原始采样信号是一样的。
(2)每一个变换之后的值是一个复数,为a+bj的形式,那这个复数是什么意思呢?
复数a+bj在坐标系中表示为(a,b),故而复数具有模和角度,我们都知道快速傅里叶变换具有“振幅谱”和“相位谱”,它其实就是通过对快速傅里叶变换得到的复数结果进一步求出来的,
那这个直接变换后的结果就是我需要的,在FFT中,得到的结果是复数,
(3)FFT得到的复数的模(即绝对值)就是对应的“振幅谱”,复数所对应的角度,就是所对应的“相位谱”,现在可以画图了。
1.3 FFT的原始频谱
N=len(fft_y) # 频率个数
x = np.arange(N)* Fs/N
abs_y=np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)
angle_y=np.angle(fft_y) #取复数的角度 import matplotlib.pyplot as plt
# 设置字体
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.subplot(1,2,1)
plt.plot(x,abs_y)
plt.title('双边振幅谱(未归一化)')
plt.subplot(1,2,2)
plt.plot(x,angle_y)
plt.title('双边相位谱(未归一化)')
plt.show()
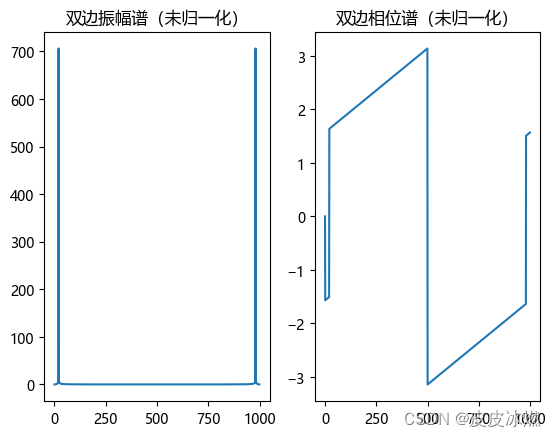
注意:我们在此处仅仅考虑“振幅谱”,不再考虑相位谱。
我们发现,振幅谱的纵坐标很大,而且具有对称性,这是怎么一回事呢?
关键:关于振幅值很大的解释以及解决办法——归一化和取一半处理。
比如有一个信号如下:
Y=A1+A2cos(2πω2+φ2)+A3cos(2πω3+φ3)+A4*cos(2πω4+φ4)
经过FFT之后,得到的“振幅图”中,
第一个峰值(频率位置)的模是A1的N倍,N为采样点,本例中为N=1000,此例中没有,因为信号没有常数项A1。
第二个峰值(频率位置)的模是A2的N/2倍,N为采样点,
第三个峰值(频率位置)的模是A3的N/2倍,N为采样点,
第四个峰值(频率位置)的模是A4的N/2倍,N为采样点,
依次下去…
考虑到数量级较大,一般进行归一化处理,既然大部分峰值是A的N/2倍,那么将每一个值都除以N/2即可。
FFT具有对称性,一般只需要用N的一半,前半部分即可。
1.4 振幅谱归一化
norm_y=abs_y/(N/2) #归一化处理(双边频谱)
plt.plot(x,norm_y,'g')
plt.title('双边频谱(归一化)',fontsize=9,color='green')
plt.show()
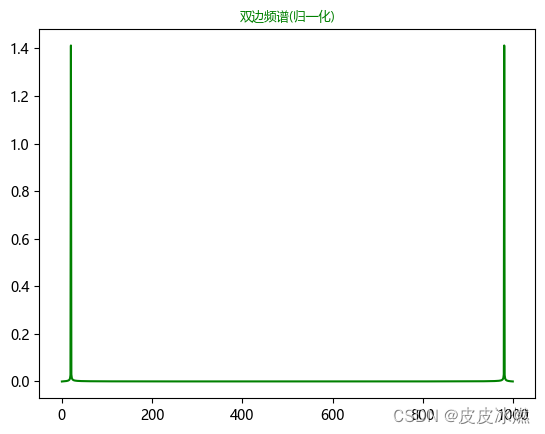
现在我们发现,振幅谱的数量级不大了,变得合理了。
1.5 取一半处理
half_x = x[range(int(N/2))] #取一半区间
norm_half_y = norm_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)
plt.plot(half_x,norm_half_y,'b')
plt.title('单边频谱(归一化)',fontsize=9,color='blue')
plt.show()
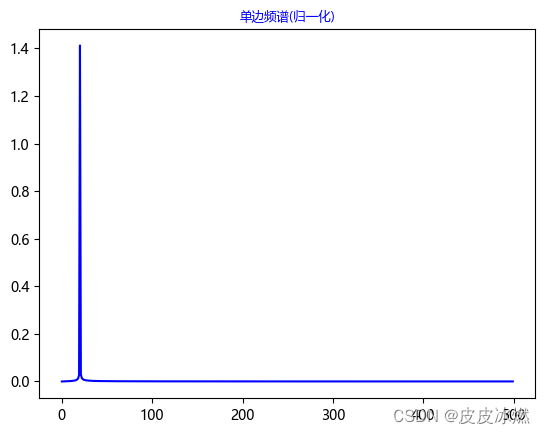
1.6 整理成一个函数my_fft()
from scipy.fftpack import fft
def my_fft(y,Fs):fft_y=fft(y) #快速傅里叶变换N=len(fft_y) # 频率个数 x = np.arange(N) * Fs/N abs_y=np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)norm_y=abs_y/(N/2) #归一化处理(双边频谱)half_x = x[range(int(N/2))] #取一半区间norm_half_y = norm_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)return half_x,norm_half_y
2 加窗
2.1 频谱泄露
统一窗函数(uniform)
汉宁窗(Hanning)
海明窗(Hamming)
布莱克窗(Blackman)
平顶窗(Flattop)
凯撒窗或凯撒贝塞尔窗(Kaiser-Bessel)
输入的数据(即“信号”)可能是周期的,也可能是非周期的。周期信号容易处理,可以将截断的长度就放在一个完整周期长度左右,这样就可以从FFT的结果里获得相应的频率信息。但是针对非周期信号,简单的截断会给FFT的计算带来一个问题,频谱泄露。
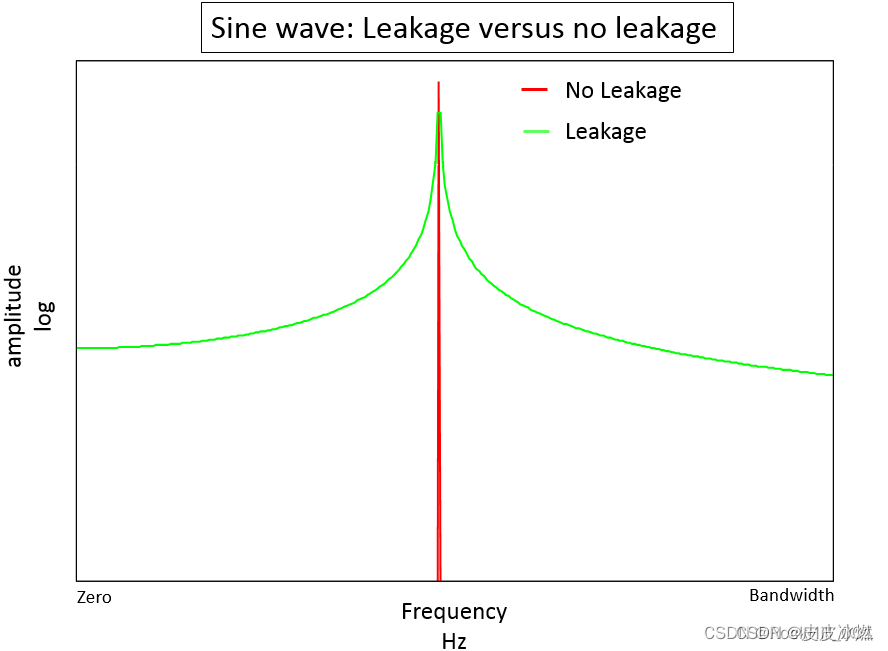
频率泄露是指原本在输入频率的幅值会被降低,而不存在于输入信号中的频率点会有幅值存在,从幅频图上“形象”的认为,分析结果从已存在频率“泄露”到了不存在的频率点上。图,红色是没有频率泄露时,绿色是存在频率泄露时。
FFT过程认为将被运算的数据无限幅值延拓后,就是原信号。所以如果截断是基于信号的周期是不会有频率泄露的,因为延拓后的信号确实等于原信号。但是如果截断的数据是非周期的,延拓后不等于原信号,则频率泄露是实际发生的。这种非周期的情况,既可以是用非周期的长度截取了周期信号,也可以是信号本身就是非周期的,二者均会发生频率泄露。解决此问题的方案是加窗,尤其是非周期信号,加窗是必须项。
加窗,简单来说,是用特殊的函数来截断数据,使得数据和函数相乘后,其结果为周期化的,减少频率泄露。常见的窗函数有以下几种。其中Uniform窗,即是简单截断,汉宁窗为比较常用的窗函数。
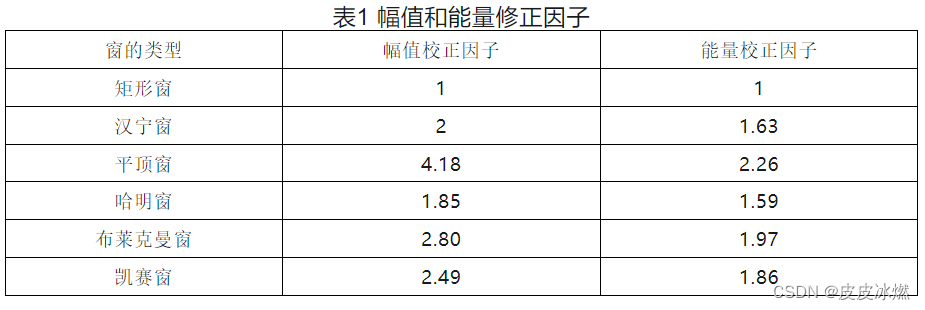
2.2 加窗FFT
from scipy.fftpack import fft
def my_fft(y,Fs):fft_y=fft(y) #快速傅里叶变换N=len(fft_y) # 频率个数 x = np.arange(N) * Fs/N abs_y=np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)norm_y=abs_y/(N/2) #归一化处理(双边频谱)half_x = x[range(int(N/2))] #取一半区间norm_half_y = norm_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)return half_x,norm_half_y# window = np.hanning(len(y)) # 汉宁窗函数,幅值修正因子为2
window = np.hamming(len(y)) # 海明窗函数,幅值修正因子为1.85
window_y = y*window # 对信号进行窗口加权
x1,y1 = my_fft(window_y,Fs)
plt.plot(x1,y1*1.85,'b')
plt.title('单边频谱(归一化)',fontsize=9,color='blue')
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude/V')
plt.show()
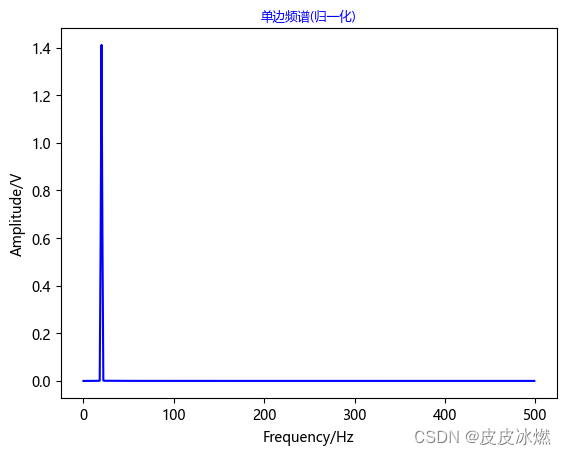
3 频谱泄露和窗函数
针对一个频率为20Hz的正玄信号,使用1000Hz的采样频率进行采样,采集10个周期的数据。
from scipy.fftpack import fft
# 设置字体
plt.rcParams['font.family'] = 'Microsoft YaHei'
def my_fft(y,Fs):fft_y=fft(y) #快速傅里叶变换N=len(fft_y) # 频率个数 x = np.arange(N)*Fs/N abs_y=np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)norm_y=abs_y/(N/2) #归一化处理(双边频谱)half_x = x[range(int(N/2))] #取一半区间norm_half_y = norm_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)return half_x,norm_half_y
3.1 周期性截断
构建一个首尾可以相接周期截断的信号。
import numpy as np
import matplotlib.pyplot as plt
fs = 1000 # 采样频率,对应周期0.001s
t_interval = 1 / fs # 频率分辨率fin = 100 # 信号频率20Hz,对应周期0.05s
n_period = 10
sample_N = int(fs / fin * 10) # 采样点数
t = np.arange(0, sample_N * t_interval, t_interval)xn = np.sqrt(2) * np.sin(2 * np.pi * fin * t) # 原始信号
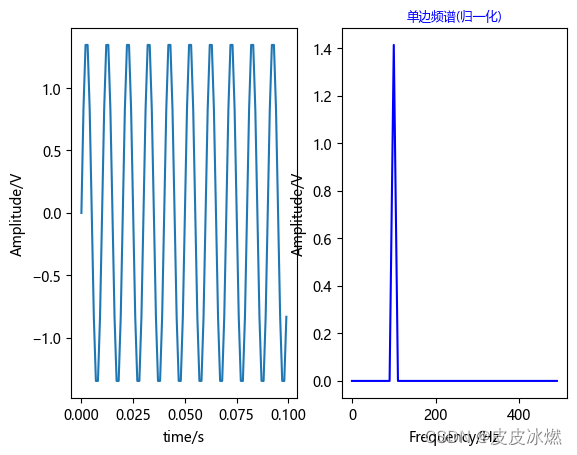
x1,y1 = my_fft(xn,fs) # fftplt.subplot(1,2,1)
plt.plot(t, xn)
plt.xlabel('time/s')
plt.ylabel('Amplitude/V')plt.subplot(1,2,2)
plt.plot(x1,y1,'b')
plt.title('单边频谱(归一化)',fontsize=9,color='blue')
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude/V')
plt.show()
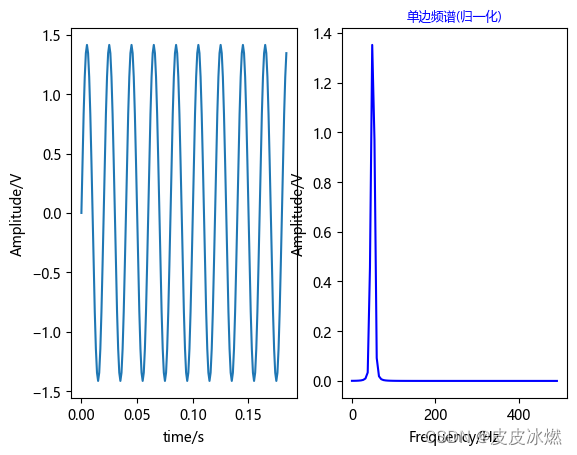
3.2 非周期截断
import numpy as np
import matplotlib.pyplot as plt
fs = 1000 # 采样频率,对应周期0.001s
t_interval = 1 / fs # 频率分辨率fin = 50 # 信号频率20Hz,对应周期0.05s
n_period = 10
sample_N = int(fs / fin * 10) # 采样点数t = np.arange(0, (sample_N - 15) * t_interval, t_interval)
xn = np.sqrt(2) * np.sin(2 * np.pi * fin * t) # 原始信号
x1,y1 = my_fft(xn,fs) # fftplt.subplot(1,2,1)
plt.plot(t, xn)
plt.xlabel('time/s')
plt.ylabel('Amplitude/V')plt.subplot(1,2,2)
plt.plot(x1,y1,'b')
plt.title('单边频谱(归一化)',fontsize=9,color='blue')
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude/V')
plt.show()
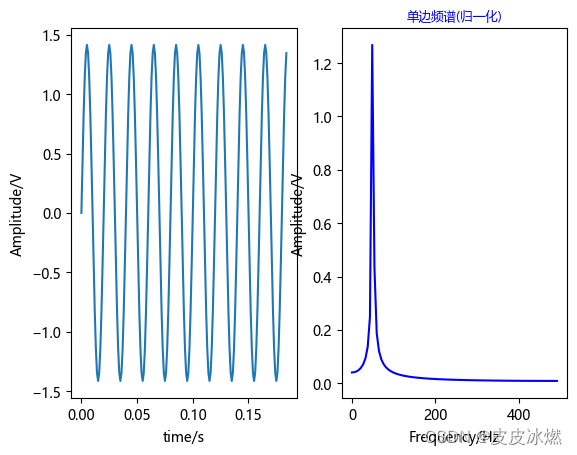
频谱泄露是由于对信号的非周期性截断所导致。
3.3 加窗处理
from scipy.fftpack import fft
# 设置字体
plt.rcParams['font.family'] = 'Microsoft YaHei'
def my_fft_window(y,Fs):window = np.hanning(len(y)) # 汉宁窗函数,幅值修正因子为2window_y = y*window # 对信号进行窗口加权fft_y=fft(window_y) #快速傅里叶变换N=len(fft_y) # 频率个数 x = np.arange(N)*Fs/N abs_y=np.abs(fft_y)*2 # 取复数的绝对值,即复数的模(双边频谱)norm_y=abs_y/(N/2) #归一化处理(双边频谱)half_x = x[range(int(N/2))] #取一半区间norm_half_y = norm_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)return half_x,norm_half_yx1,y1 = my_fft_window(xn,fs) # fft
plt.subplot(1,2,1)
plt.plot(t, xn)
plt.xlabel('time/s')
plt.ylabel('Amplitude/V')plt.subplot(1,2,2)
plt.plot(x1,y1,'b')
plt.title('单边频谱(归一化)',fontsize=9,color='blue')
plt.xlabel('Frequency/Hz')
plt.ylabel('Amplitude/V')
plt.show()