对应视频链接点击直达
01项目点击下载,可直接运行(含数据库)
05眼动识别软件详情2
- 对应视频链接点击直达
- 期望的数据展示
- 数据波形对比
- 如何实现
- 几种常用滤波介绍
- 维纳滤波
- 巴特沃斯滤波器
- 中值滤波
- 排序滤波
- 推荐
- 结语
- 其他
- 以下是废话
原始数据的波形,简直没法看!
这章来说说波形的优化,让数据展示明显!
期望的数据展示
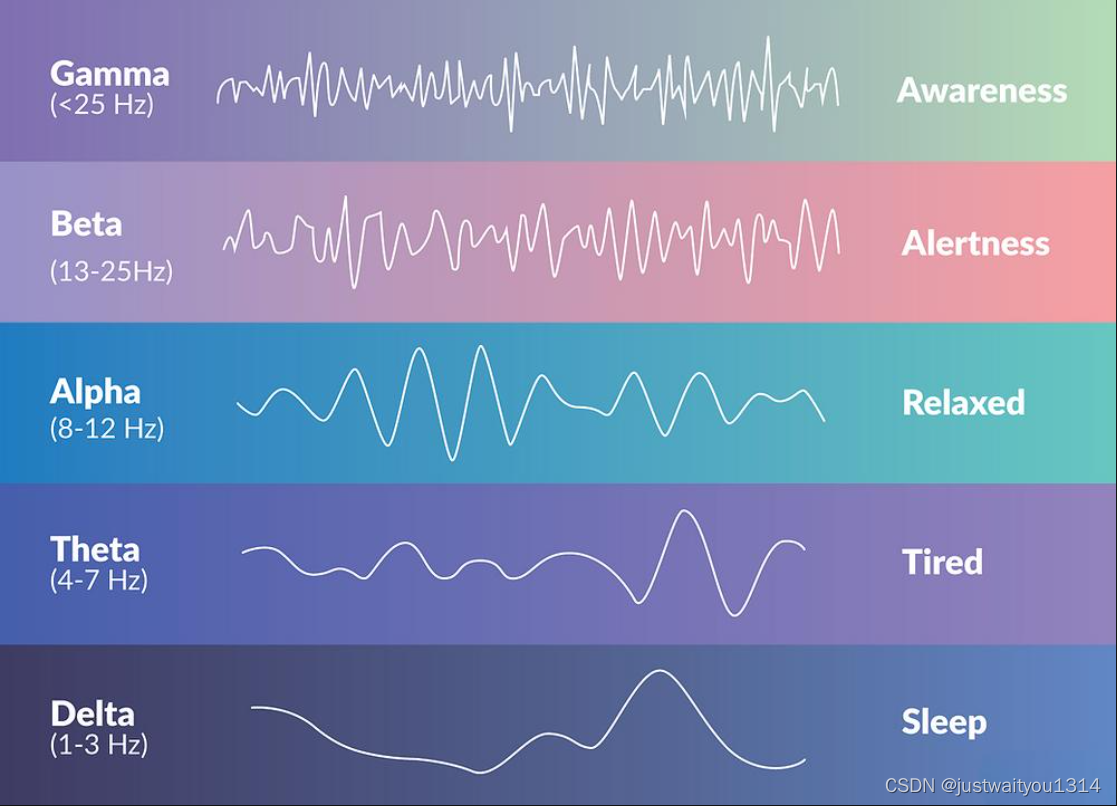
数据波形对比
同类型数据,无滤波

同类型数据,有滤波

主观的说,下面的数据,人能看···
如何实现
几种常用滤波介绍
维纳滤波
信号经过系统之后,相当于进行了卷积操作,若想让其复原,只需再用系统进行反卷积即可。如果没有信号,系统却有了响应,那么这种噪声可以理解为系统的噪声。如果系统的数学形式是已知的,这种噪声就很容易滤掉,如果未知,那就需要进行估计,这就是维纳做的工作。
一个有限脉冲响应(finite impulse response, FIR),其离散形式可通过卷积表示为

x=sin(1.5πt(1−t)+2.1)+0.1sin(2.5πt+1)+0.18cos(7.6πt)
import numpy as np
import scipy.signal as sst = np.linspace(-1, 1, 201)
PI = 2*np.pi
x = (np.sin(PI*0.75*t*(1-t) + 2.1) +0.1*np.sin(PI*1.25*t + 1) +0.18*np.cos(PI*3.85*t))# 原始数据添加噪声
np.random.seed(42)
xn = x + np.random.rand(len(t))w = ss.wiener(xn, 9) # 维纳滤波plt.scatter(t, xn, marker='.', label="original")
plt.plot(t, w, c = 'r', label="wiener")
plt.legend()
plt.show()
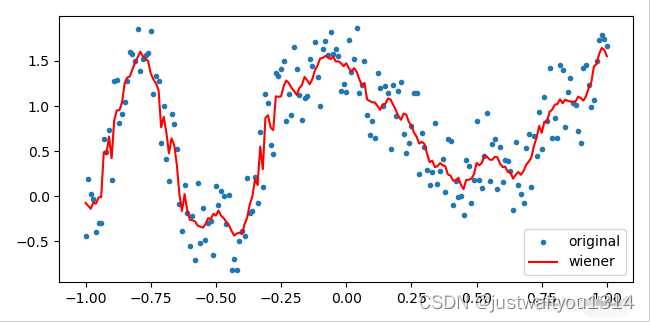
wiener是signal模块中的滤波函数,其输入参数分别是待滤波数据和滤波模板,此外还有一个noise,表示系统噪声,默认为None,表示自行估计噪声。
巴特沃斯滤波器
FIR的特点是无反馈,yn 完全由xn决定,如果响应受到反馈的影响,便是无限脉冲响应(infinite impulse response, IIR),其离散形式变为
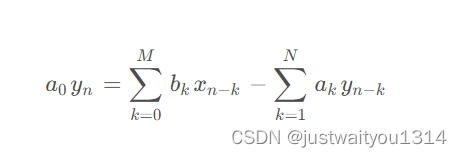
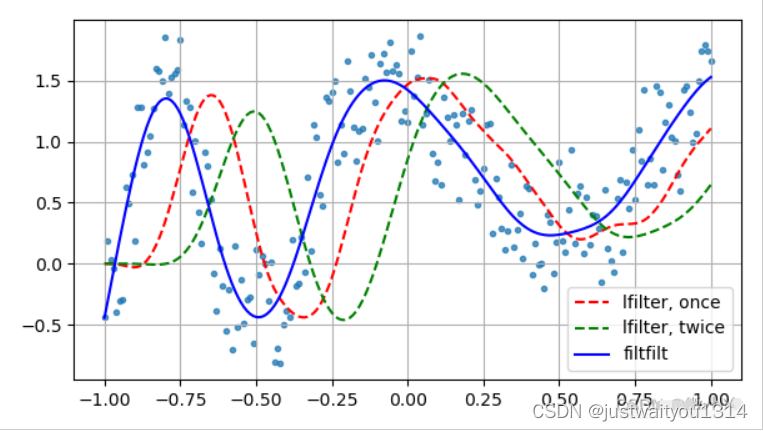
滤波器设计,就是对ak,bk具体形式的求解,signal模块中提供了一些函数,对这两种信号进行滤波。仍以函数x为例,在添加噪声之后,进行滤波,对于不同的滤波函数,其效果如下
import scipy.signal as ss
import matplotlib.pyplot as pltb, a = ss.butter(3, 0.05)
z = ss.lfilter(b, a, xn)
z2 = ss.lfilter(b, a, z)
z3 = ss.filtfilt(b, a, xn)# 下面为绘图代码
plt.plot(t, z, 'r--', label="lfilter, once")
plt.plot(t, z2, 'g--', label="lfilter, twice")
plt.plot(t, z3, 'b', label="filtfilt")
plt.scatter(t, xn, marker='.', alpha=0.75)plt.grid()
plt.legend()
plt.show()
butter函数生成3阶巴特沃斯滤波器对应的 aaa和bbb值
lfilter是最基础的脉冲响应滤波器,从左侧开始进行滤波,故而会产生相位差
filtfilt从正反两个方向滤波,可消除了lfilter产生的相位差
中值滤波
中值滤波,就是挑选出将个滤波模板范围内数据的中位数,例如[1,3,2,4]这个数组,给定一个长度为3的滤波窗口,那么元素3所在位置的滤波范围就是1,3,2,其中位数是2,所以要把3更改为2。
import numpy as np
import scipy.signal as ss
x = [1,3,2,4]
ss.medfilt(x,3) # [1, 2, 3, 2]
二维的中值滤波在图像处理中非常常见,对椒盐噪声有着非常霸道的滤除效果。所谓椒盐噪声,如下方左图所示,就是图像中随机产生的黑色和白色的斑点。在使用二维的中值滤波之后,整张图片都变得清澈了。

参考代码:
from scipy.misc import ascent
import matplotlib.pyplot as pltimg = ascent()
img = img[:256, :256]
r = np.random.rand(*img.shape)
img[r>0.96] = 255
img[r<0.04] = 0plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.axis('off')plt.subplot(122)
imFilt = ss.medfilt2d(img, [3,3])
plt.imshow(imFilt, cmap='gray')
plt.axis('off')plt.show()
排序滤波
排序滤波是中值滤波概念的扩充,和中值滤波的区别是,在对滤波窗口中的数据进行排序之后,可以指定用以替代当前数据的数值序号。下面四个矩阵,展示了以3×3单位矩阵为滤波模板,排序滤波在不同排序参数下的结果。
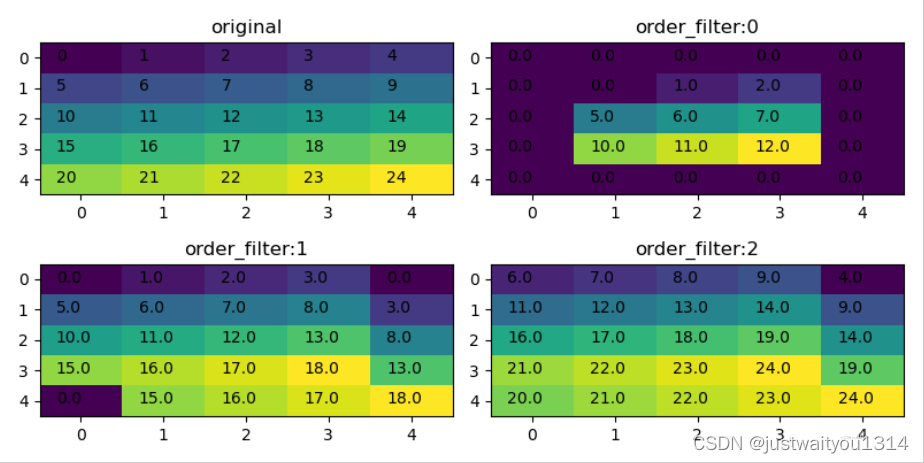
此滤波过程在scipy中的实现方式如下:
x = np.arange(25).reshape(5, 5).astype(float)
I = np.identity(3)mats = {"original":x}
for i in range(3):mats[f"order_filter:{i}"] = ss.order_filter(x, I, i)
order_filter】即为signal模块提供的排序滤波函数,以输入参数(x, I, i)为例,表示从矩阵x中选出单位阵I所覆盖区域中第i小的元素。I是一个单位阵,就实际情况来看,其覆盖的第一个子阵中,以0为中心,则只能覆盖到2x2的范围,对角元素0,6,最小值是0,最大值是6。如以6为中心,则可以完全覆盖3x3的内容,最小值为0,最大值为12。
绘图代码如下:
def drawMat(x, ax=None):M, N = x.shapeif not ax:ax = plt.subplot()arrM, arrN = np.arange(M), np.arange(N)plt.yticks(arrM+0.5, arrM)plt.xticks(arrN+0.5, arrN)ax.pcolormesh(x)ax.invert_yaxis()for i,j in product(range(M),range(N)):ax.text(j+0.2, i+0.6, f"{x[i,j]}")for i,key in enumerate(mats,1):ax = plt.subplot(2,2,i)drawMat(mats[key], ax)plt.title(key)plt.show()
推荐
我这边推荐使用FIR或者IIR
我这边的代码如下:
import numpy as npdef baseline_correction(eog_signal, sampling_rate):# 计算信号的时间数组nm = int(len(eog_signal) / 4)eog_signal1 = eog_signalbaseline_corrected = []for i in range(4):eog_signal = eog_signal1[i * nm:(i + 1) * nm]time = np.arange(len(eog_signal)) / sampling_rate # 算出这个数据的时间 并生成数组# 使用线性回归估计基线趋势coefficients = np.polyfit(time, eog_signal, 1)# 生成基线趋势baseline_trend = coefficients[0] * time + coefficients[1]# 从原始信号中减去基线趋势以进行校正baseline_corrected1 = eog_signal - baseline_trendbaseline_corrected.extend(baseline_corrected1)return baseline_corrected# 将数据转换为numpy数组fs = 256 # 举例:1000Hz# 设计FIR滤波器fir_freq = np.array([0.1, 45]) / (fs / 2) # 将8-13Hz转换为归一化频率# 线性回归极限矫正以后的数据data_baseline = baseline_correction(eye_data, fs)应用FIR滤波器1fir_coeff = signal.firwin(numtaps=7, cutoff=fir_freq, pass_zero=False) # 阶数指的是 numtaps - 1fir_filtered_data = signal.lfilter(fir_coeff, 1, data_baseline) # 无反馈 滤波器 第二组系数全是1 输出只与当前和过去输入有关,与过去输出无关# 应用IIR滤波器2iir_coeff = signal.iirfilter(N=5, Wn=fir_freq, btype='band', ftype='butter')fir_filtered_data = signal.lfilter(iir_coeff[0], iir_coeff[1], data_baseline)
结语
其他
以上仅作参考,欢迎一起讨论!
V:justwaityou1314
懂的都懂
以下是废话
别的也没啥说的 , 如果觉得可以 , 希望一键三连支持一下我的B站作品
欢迎各位大佬留言吐槽,也可以深入科学探讨






![[vue2]深入理解路由](https://img-blog.csdnimg.cn/img_convert/552275e60449aceaeb7c47442dc61c93.png)