目录
累积弹性曲线
累积增益曲线
考虑差异
关键思想
累积弹性曲线
再次考虑将价格转换为二元处理的说明性示例。我们会从我们离开的地方拿走它,所以我们有弹性处理带。我们接下来可以做的是根据乐队的敏感程度对乐队进行排序。也就是说,我们把最敏感的组放在第一位,第二个最敏感的组放在第二位,依此类推。对于模型 1 和 3,无需重新订购,因为它们已经订购。对于模型 2,我们必须颠倒排序。
一旦我们有了有序的组,我们就可以构建我们称之为累积弹性曲线的东西。我们首先计算第一组的弹性;然后,第一个和第二个等等,直到我们包含所有组。最后,我们将只计算整个数据集的弹性。这是我们的说明性示例的外观。
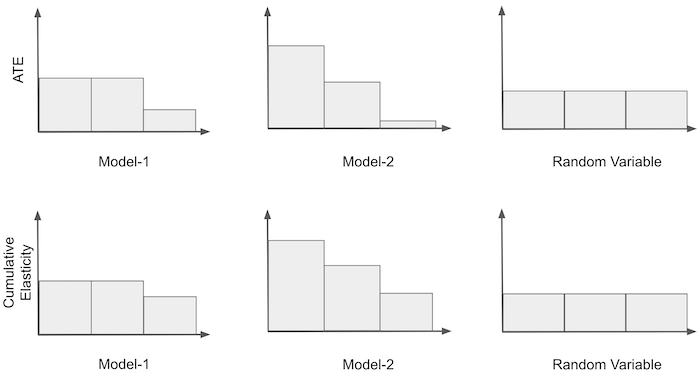
请注意,累积弹性中的第一个 bin 只是根据该模型来自最敏感组的 ATE。此外,对于所有模型,累积弹性将收敛到同一点,即整个数据集的 ATE。
在数学上,我们可以将累积弹性定义为直到单位 k 之前估计的弹性。
为了构建累积弹性曲线,我们在数据集中迭代地运行上述函数以产生以下序列。
就模型评估而言,这是一个非常有趣的序列,因为我们可以对其进行偏好陈述。首先,模型更好的程度
对于任何 k 和 a>0。换句话说,如果一个模型擅长对弹性进行排序,那么在前 k个样本中观察到的弹性应该高于在前 k+a 个样本中观察到的弹性。或者,简单地说,如果我查看顶部单位,它们应该比它们下面的单位具有更高的弹性。
其次,模型更好的程度
是最大的,对于任何 k 和 a>0。直觉是,我们不仅希望顶部 k 单位的弹性高于其下方单位的弹性,而且我们希望这种差异尽可能大。
为了使其更具体,这是用代码表示的这个想法。
def cumulative_elast_curve(dataset, prediction, y, t, min_periods=30, steps=100):size = dataset.shape[0]# orders the dataset by the `prediction` columnordered_df = dataset.sort_values(prediction, ascending=False).reset_index(drop=True)# create a sequence of row numbers that will define our Ks# The last item is the sequence is all the rows (the size of the dataset)n_rows = list(range(min_periods, size, size // steps)) + [size]# cumulative computes the elasticity. First for the top min_periods units.# then for the top (min_periods + step*1), then (min_periods + step*2) and so onreturn np.array([elast(ordered_df.head(rows), y, t) for rows in n_rows])关于此功能的一些注意事项。 它假定对弹性进行排序的事物存储在传递给“预测”参数的列中。 此外,第一组有 min_periods 单位,因此它可以与其他组不同。 原因是,由于样本量小,弹性在曲线开始时可能过于嘈杂。 为了解决这个问题,我们可以传递一个已经足够大的第一组。 最后,steps 参数定义了我们在每个后续组中包含多少额外单元。
使用此功能,我们现在可以根据每个模型产生的顺序绘制累积弹性曲线。
plt.figure(figsize=(10,6))for m in range(3):cumu_elast = cumulative_elast_curve(prices_rnd_pred, f"m{m+1}_pred", "sales", "price", min_periods=100, steps=100)x = np.array(range(len(cumu_elast)))plt.plot(x/x.max(), cumu_elast, label=f"M{m+1}")plt.hlines(elast(prices_rnd_pred, "sales", "price"), 0, 1, linestyles="--", color="black", label="Avg. Elast.")
plt.xlabel("% of Top Elast. Days")
plt.ylabel("Cumulative Elasticity")
plt.title("Cumulative Elasticity Curve")
plt.legend();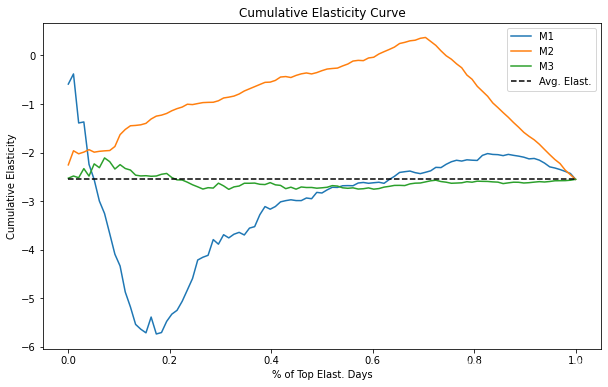
解释累积弹性曲线可能有点挑战性,但这是我的看法。同样,考虑二分类情况可能更容易。曲线的 X 轴代表我们正在处理的样本数量。在这里,我将轴归一化为数据集的比例,所以 0.4 意味着我们正在处理 40% 的样本。 Y 轴是我们在这么多样本上应该预期的弹性。因此,如果一条曲线在 40% 处的值为 -1,则意味着前 40% 单位的弹性为 -1。理想情况下,我们希望尽可能大的样本具有最高的弹性。理想的曲线将在 Y 轴上从高处开始,然后非常缓慢地下降到平均弹性,这表示我们可以处理高百分比的单位,同时仍保持高于平均弹性。
不用说,我们的模型都没有接近理想的弹性曲线。随机模型 M3 围绕平均弹性波动,并且永远不会离它太远。这意味着该模型无法找到弹性与平均弹性不同的组。至于预测模型 M1,它似乎是反向排序的弹性,因为曲线从低于平均弹性开始。不仅如此,它还在大约 50% 的样本处很快收敛到平均弹性。最后,因果模型 M2 似乎更有趣。一开始它有这种奇怪的行为,累积弹性增加远离平均值,但随后它达到了一个点,我们可以处理大约 75% 的单位,同时保持几乎为 0 的相当不错的弹性。这可能是因为这个模型可以识别非常低弹性(高价格敏感度)的日子。因此,如果我们在那些日子不提价,我们可以对大部分样本(约 75%)进行提价,同时价格敏感度仍然较低。
在模型评估方面,累积弹性曲线(Cumulative Elasticity Curve) 已经远远好于简单的分区间的弹性概念。在这里,我们设法对我们的模型做出更精确的偏好陈述。不过,这是一条复杂的曲线,难以理解。出于这个原因,我们可以做进一步的改进。
累积增益曲线
下一个想法是在累积弹性之上进行非常简单但强大的改进。我们将累积弹性乘以比例样本量。例如,如果累积弹性在 40% 时为 -0.5,那么此时我们将得到 -0.2 (-0.5 * 0.4)。然后,我们将其与随机模型产生的理论曲线进行比较。这条曲线实际上是一条从 0 到平均干预效果的直线。可以这样想:随机模型的累积弹性中的每个点都是 ATE,因为该模型只生成数据的随机代表性分区。如果在 (0,1) 线上的每一点,我们将 ATE 乘以该点,我们最终会得到一条介于 0 和 ATE 之间的直线。
一旦我们有了理论上的随机曲线,我们就可以将其用作基准,并将我们的其他模型与它进行比较。所有曲线将在同一点开始和结束。然而,模型的弹性排序越好,曲线在零到一之间的点处偏离随机线的程度就越大。例如,在上图中,M2 优于 M1,因为它在到达终点 ATE 之前发散得更多。对于熟悉 ROC 曲线的人,您可以将累积增益视为因果模型的 ROC。
从数学上讲,
要在代码中实现它,我们所要做的就是添加比例样本大小归一化。
def cumulative_gain(dataset, prediction, y, t, min_periods=30, steps=100):size = dataset.shape[0]ordered_df = dataset.sort_values(prediction, ascending=False).reset_index(drop=True)n_rows = list(range(min_periods, size, size // steps)) + [size]## add (rows/size) as a normalizer. return np.array([elast(ordered_df.head(rows), y, t) * (rows/size) for rows in n_rows])使用我们的冰激凌数据,我们会得到如下曲线。
plt.figure(figsize=(10,6))for m in range(3):cumu_gain = cumulative_gain(prices_rnd_pred, f"m{m+1}_pred", "sales", "price", min_periods=50, steps=100)x = np.array(range(len(cumu_gain)))plt.plot(x/x.max(), cumu_gain, label=f"M{m+1}")plt.plot([0, 1], [0, elast(prices_rnd_pred, "sales", "price")], linestyle="--", label="Random Model", color="black")plt.xlabel("% of Top Elast. Days")
plt.ylabel("Cumulative Gain")
plt.title("Cumulative Gain")
plt.legend();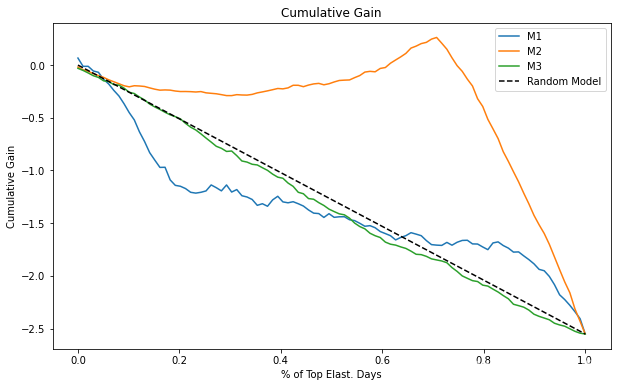
现在很清楚,因果模型(M2)比其他两个要好得多。它与随机线的差异远大于 M1 和 M3。此外,请注意随机模型 M3 如何非常接近理论随机模型。两者之间的区别可能只是随机噪声。
有了这个,我们介绍了一些关于如何评估因果模型的非常好的想法。仅此一项就是一件大事。即使我们没有要比较的基本事实,我们也设法评估了模型在排序弹性方面的好坏。只缺少最后一件事,即包括围绕这些测量值的置信区间。毕竟,我们不是野蛮人,不是吗?
考虑差异
当我们处理弹性曲线时,不考虑方差是错误的。特别是由于它们都使用线性回归理论,因此在它们周围添加置信区间应该相当容易。
为此,我们将首先创建一个函数,该函数返回线性回归参数的 CI。我在这里使用简单线性回归的公式,但可以随意提取 CI。
def elast_ci(df, y, t, z=1.96):n = df.shape[0]t_bar = df[t].mean()beta1 = elast(df, y, t)beta0 = df[y].mean() - beta1 * t_bare = df[y] - (beta0 + beta1*df[t])se = np.sqrt(((1/(n-2))*np.sum(e**2))/np.sum((df[t]-t_bar)**2))return np.array([beta1 - z*se, beta1 + z*se])通过对我们的cumulative_elast_curve函数进行一些小的修改,我们可以输出弹性的置信区间。
def cumulative_elast_curve_ci(dataset, prediction, y, t, min_periods=30, steps=100):size = dataset.shape[0]ordered_df = dataset.sort_values(prediction, ascending=False).reset_index(drop=True)n_rows = list(range(min_periods, size, size // steps)) + [size]# just replacing a call to `elast` by a call to `elast_ci`return np.array([elast_ci(ordered_df.head(rows), y, t) for rows in n_rows])最后,这是因果 (M2) 模型的 95% CI 的累积弹性曲线。
plt.figure(figsize=(10,6))cumu_gain_ci = cumulative_elast_curve_ci(prices_rnd_pred, "m2_pred", "sales", "price", min_periods=50, steps=200)
x = np.array(range(len(cumu_gain_ci)))
plt.plot(x/x.max(), cumu_gain_ci, color="C0")plt.hlines(elast(prices_rnd_pred, "sales", "price"), 0, 1, linestyles="--", color="black", label="Avg. Elast.")plt.xlabel("% of Top Elast. Days")
plt.ylabel("Cumulative Elasticity")
plt.title("Cumulative Elasticity for M2 with 95% CI")
plt.legend();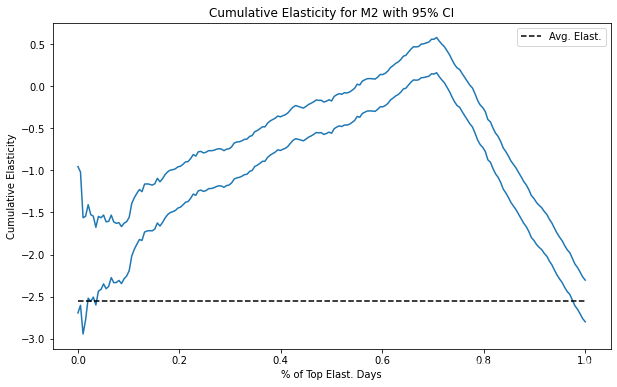
注意随着我们积累更多的数据集,CI 是如何变得越来越小的。 那是因为样本量增加了。
至于累积增益曲线,获取 CI 也同样简单。 同样,我们只是将调用 elast 函数替换为调用 elast_ci 函数。
def cumulative_gain_ci(dataset, prediction, y, t, min_periods=30, steps=100):size = dataset.shape[0]ordered_df = dataset.sort_values(prediction, ascending=False).reset_index(drop=True)n_rows = list(range(min_periods, size, size // steps)) + [size]return np.array([elast_ci(ordered_df.head(rows), y, t) * (rows/size) for rows in n_rows])这是因果模型的样子。 请注意,现在 CI 开始时很小,即使曲线开始时的样本量较小。 原因是归一化因子 回避了 ATE 参数,并且它是 CI。 由于这条曲线应该用于比较模型,所以这应该不是问题,因为曲线会将这个推卸因子平等地应用于所有正在评估的模型。
plt.figure(figsize=(10,6))cumu_gain = cumulative_gain_ci(prices_rnd_pred, "m2_pred", "sales", "price", min_periods=50, steps=200)
x = np.array(range(len(cumu_gain)))
plt.plot(x/x.max(), cumu_gain, color="C0")plt.plot([0, 1], [0, elast(prices_rnd_pred, "sales", "price")], linestyle="--", label="Random Model", color="black")plt.xlabel("% of Top Elast. Days")
plt.ylabel("Cumulative Gain")
plt.title("Cumulative Gain for M2 with 95% CI")
plt.legend();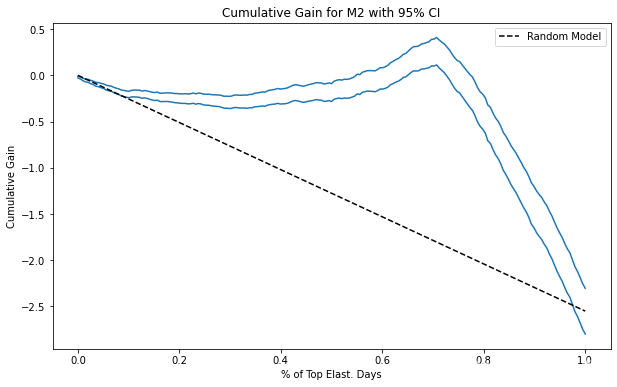
关键思想
在这里,我们看到了三种方法来检查模型在排序弹性方面的好坏。我们使用这些方法来比较和决定具有因果关系的模型。这是非常重要的。我们已经设法检查了一个模型是否擅长识别具有不同弹性的组,即使无法看到弹性!
在这里,我们严重依赖随机数据。我们在非随机数据上训练了模型,但所有评估都是在随机处理的样本上完成的。那是因为我们需要某种方法来自信地估计弹性。如果没有随机数据,我们在这里使用的简单公式将不起作用。正如我们现在非常清楚的那样,简单的线性回归在存在混杂变量的情况下忽略了变量偏差。