QT自定义标题栏窗口其二:实现拖动及可拉伸效果 + 顶部全屏/侧边半屏
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/354975.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
学习笔记——网络管理与运维——SNMP(基本配置)
四、SNMP基本配置 1、SNMP配置举例 整个华为数通学习笔记系列中,本人是以网络视频与网络文章的方式自学的,并按自己理解的方式总结了学习笔记,某些笔记段落中可能有部分文字或图片与网络中有雷同,并非抄袭。完处于学习态度&#x…
蓝鹏测控公司全长直线度算法项目多部门现场组织验收
关键字:全场直线度算法,直线度测量仪,直线度检测,直线度测量设备, 6月18日上午,蓝鹏测控公司全长直线度算法项目顺利通过多部门现场验收。该项目由公司技术部、开发部、生产部等多个部门共同参与,旨在提高直线度测量精度,满足高精度制造领域需…
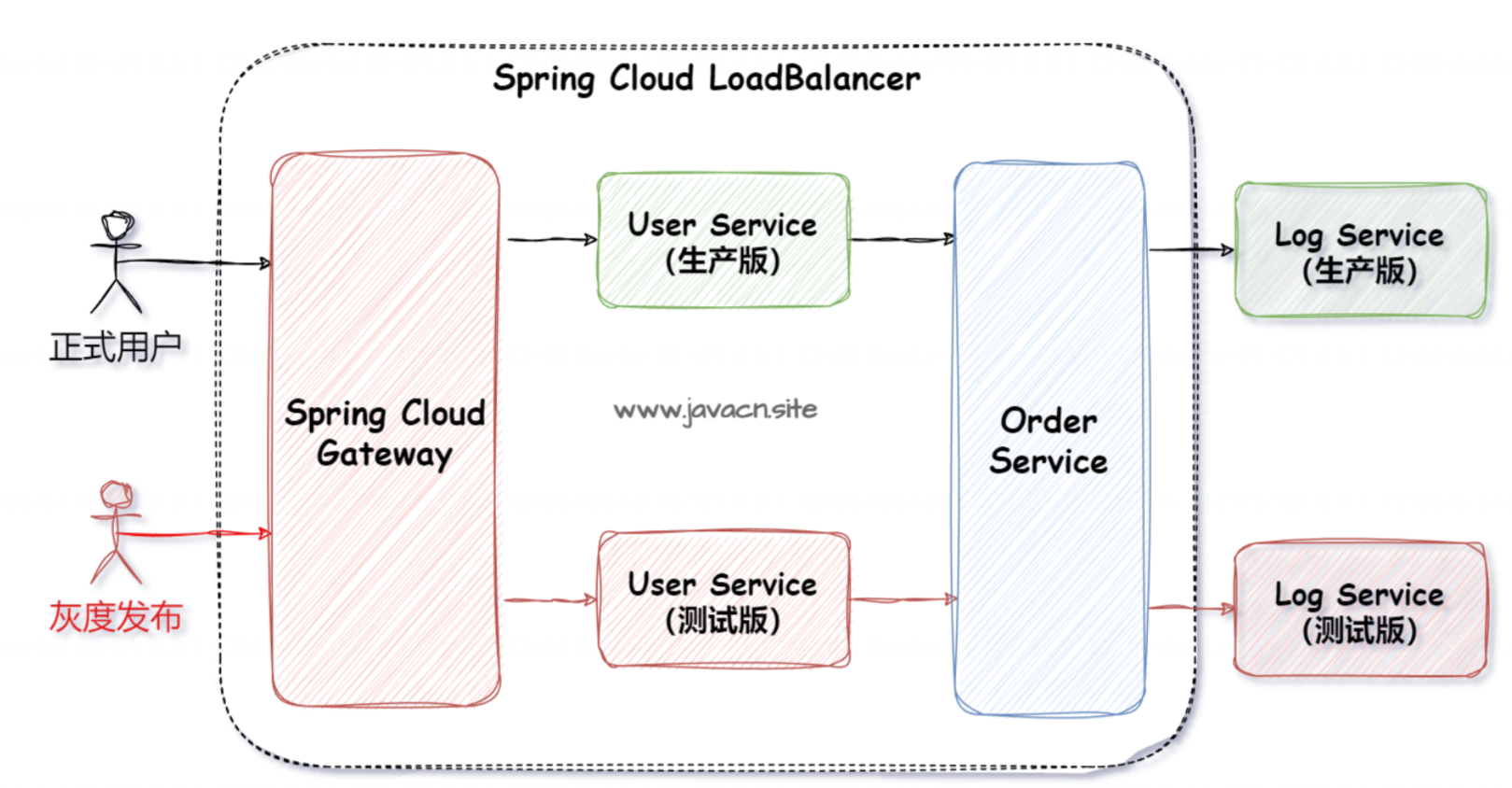
Spring Cloud全家桶(上)【Nacos、OpenFeign、LoadBalancer、GateWay、金丝雀灰色发布】
0.零基础入门微服务实战课 1.微服务和 Spring Cloud1.1 什么是微服务?1.2 什么是 Spring Cloud?1.3 微服务 VS Spring Cloud 2.为什么要学微服务?3.Spring Cloud 组件介绍1.什么是 Nacos?1.1 Nacos 功能1.1.1 配置中心1.1.2 注册中心 1.2 Na…
2024年6月20日 (周四) 叶子游戏新闻
超市播音系统: 定时播放不同音乐 强制卸载软件: 一款强制卸载软件 免费多人沙盒游戏《宝藏世界》推出更新“潮起潮落”,带来全新克苏鲁风冒险准备好迎接一场超凡的冒险吧,MMORPG发行商gamigo宣布《宝藏世界》的最新更新:“潮起潮落”。这次更…
模拟原神圣遗物系统-小森设计项目,设计圣遗物(生之花,死之羽,时之沙,空之杯,理之冠)抽象类
分析圣遗物
在圣遗物系统,玩家操控的是圣遗物的部分
因此我们应该 物以类聚 人与群分把每个圣遗物的部分,抽象出来 拿 生之花,死之羽为例 若是抽象 类很好的扩展 添加冒险家的生之花 时候继承生之花 并且名称冒险者- 生之花 当然圣遗物包含…
Pikachu靶场--RCE
参考借鉴 pikachu-RCE_pikachu rce-CSDN博客 Pikachu靶场-RCE远程命令/代码执行漏洞-CSDN博客 命令执行/代码执行/RCE(CTF教程,Web安全渗透入门)_bilibili exec"ping"
输入IP地址查看页面反应 可以在IP地址的后面拼接我们想要执行…
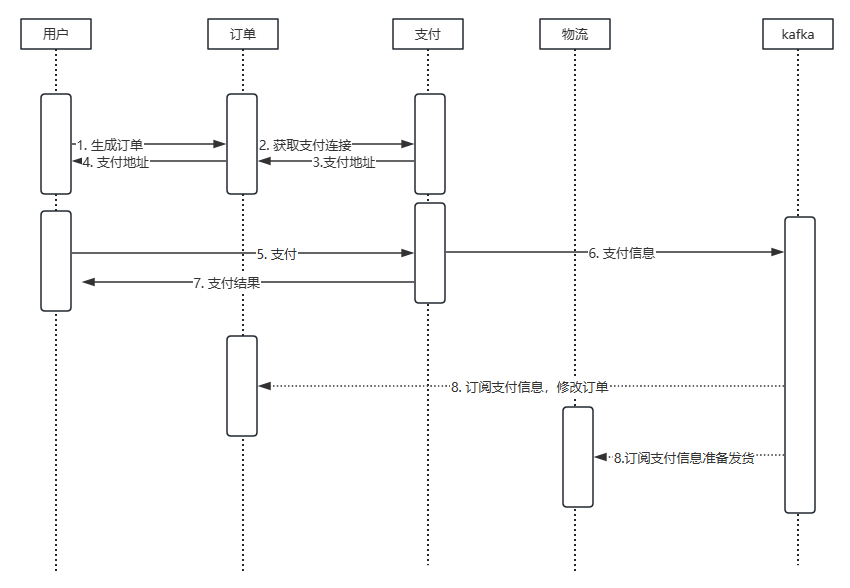
【全开源】快递寄件小程序源码(FastAdmin+ThinkPHP+原生微信小程序)
📦快递寄件小程序:轻松寄送,便捷生活
🚚一、引言:告别繁琐,让寄件更简单
在繁忙的生活中,寄送快递往往成为我们的一大难题。传统的寄件方式需要前往快递公司网点,填写繁琐的寄件信…
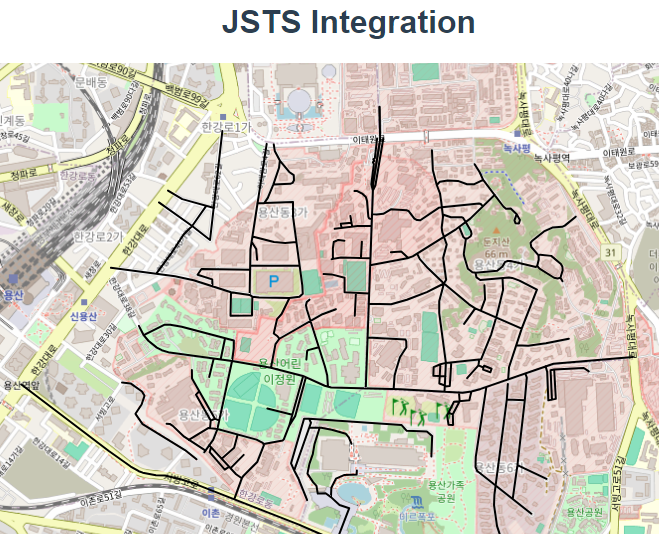
五十、openlayers官网示例JSTS Integration解析——使用JSTS 库来处理几何缓冲区并在地图上显示结果
官网demo地址: JSTS Integration 这篇讲了如何在地图上添加缓冲图形
什么叫做缓冲几何?
几何缓冲(Geometric Buffering)是指在 GIS(地理信息系统)和计算几何中,围绕一个几何对象创建一个具有…
eclipse 老的s2sh(Struts2+Spring+Hibernate) 项目 用import导入直接导致死机(CPU100%)的解决
1、下载Apache Tomcat - Apache Tomcat 8 Software Downloads
图中是8.5.100的版本,下面的设置用的是另一个版本的,其实是一样。
2、先将Server配好,然后再进行导入操作。 2、选择jdk 当然,这里也可以直接“Download and instal…
【Unity设计模式】状态编程模式
前言
最近在学习Unity游戏设计模式,看到两本比较适合入门的书,一本是unity官方的 《Level up your programming with game programming patterns》 ,另一本是 《游戏编程模式》
这两本书介绍了大部分会使用到的设计模式,因此很值得学习
本…
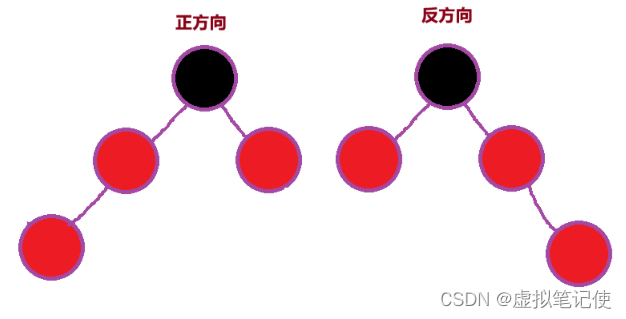
【数据结构】红黑树实现详解
在本篇博客中,作者将会带领你使用C来实现一棵红黑树,此红黑树的实现是基于二叉搜索树和AVLTree一块来讲的,所以在看本篇博客之前,你可以先看看下面这两篇博客 【C】二叉搜索树-CSDN博客 【数据结构】AVLTree实现详解-CSDN博客 在这…
使用opencv合并两个图像
本节的目的
linear blending(线性混合)使用**addWeighted()**来添加两个图像
原理
(其实我也没太懂,留个坑,感觉本科的时候线代没学好。不对,我本科就没学线代。) 源码分析
源码链接
#include "opencv2/imgc…
从0进入微服务需要了解的基础知识
文章目录 系统架构演化过程为什么要了解系统架构的演化过程技术发展认知技术选型与创新 演变过程单体架构分层-分布式集群微服务 分布式\集群\微服务 微服务中的核心要素-拆分原则项目拆分与复杂度微服务的拆分维度有哪些小结 微服务中的核心要素服务化进行拆分后一定是微服务&…
Unity和UE免费领恐怖书本头怪兽角色模型恐怖或奇幻游戏monster适合FPS类型PBR202406202143
Unity和UE免费领恐怖书本头怪兽角色模型恐怖或奇幻游戏monster适合FPS类型PBR202406202143 Unity恐怖书本头怪兽角色模型:https://prf.hn/l/zpBqgVl
UE恐怖书本头怪兽角色模型:https://prf.hn/l/4PzY1Qy
作者其他资产:https://prf.hn/l/0…
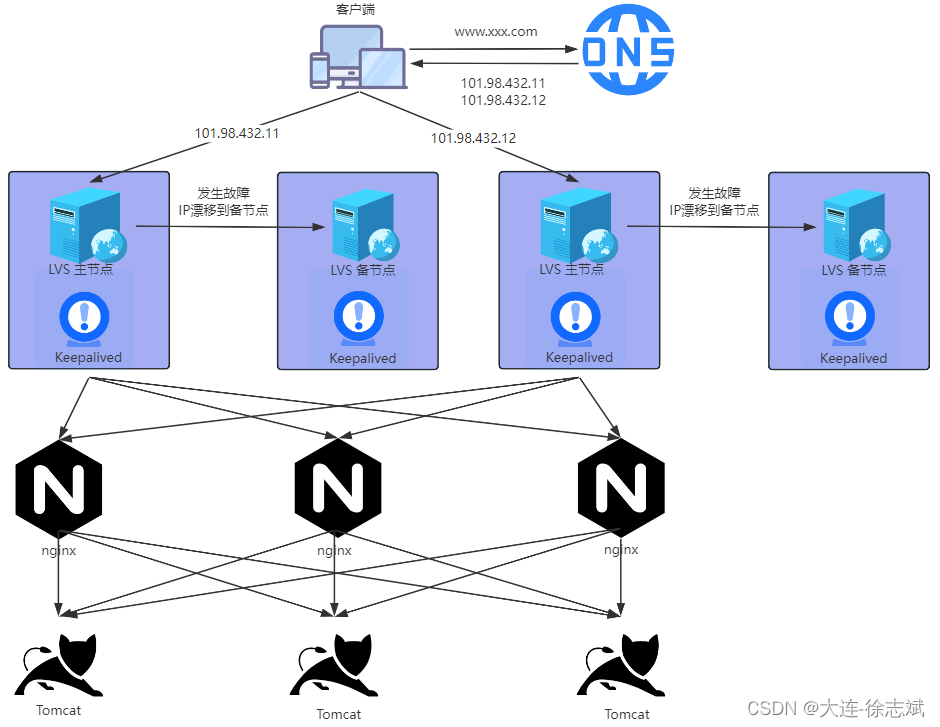
百万级 QPS 接入层网关架构方案演进
文章目录 前言1、单机架构2、DNS 轮询3、Nginx 单机4、Nginx 主备 Keepalived5、LVS 主备 Keepalived Nginx 集群6、LVS 主备 Keepalived Nginx 集群 DNS 轮询 前言
随着PC、移动互联网的快速发展,越来越多的人通过手机、电脑、平板等设备访问各种各样APP、网…
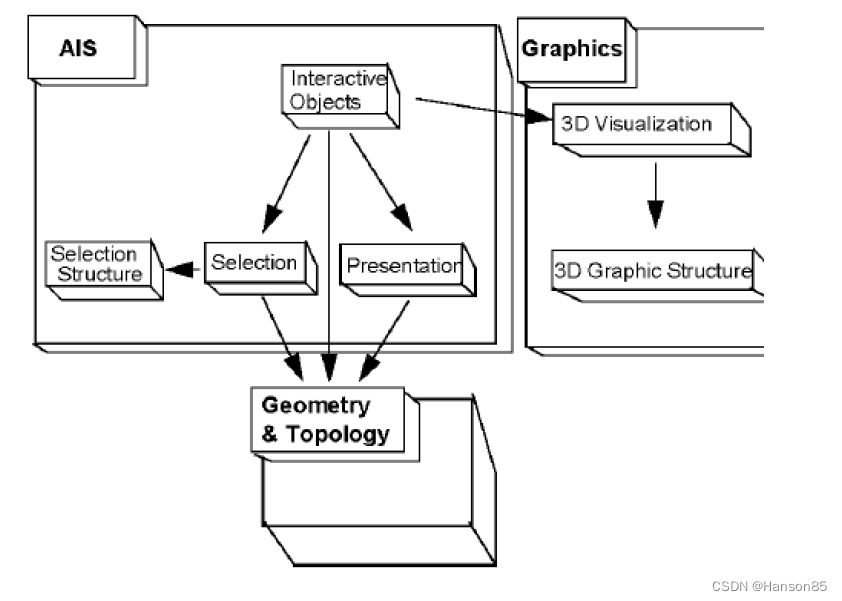
OCC介绍及框架分析
1.OCC介绍
Open CASCADE (简称OCC)是一开源的几何造型引擎,OCCT库是由Open CASCADE公司开发和市场运作的。它是为开源社区比较成熟的基于BREP结构的建模引擎,能够满足二维三维实体造型和曲面造型,国内研究和使用它的单…
[论文笔记]Are Large Language Models All You Need for Task-Oriented Dialogue?
引言
今天带来论文Are Large Language Models All You Need for Task-Oriented Dialogue?的笔记。
主要评估了LLM在完成多轮对话任务以及同外部数据库进行交互的能力。在明确的信念状态跟踪方面,LLMs的表现不及专门的任务特定模型。然而,如果为它们提…
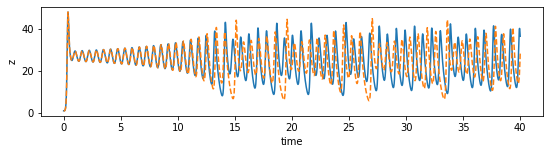
【机器学习】基于稀疏识别方法的洛伦兹混沌系统预测
1. 引言
1.1. DNN模型的来由
从数据中识别非线性动态学意味着什么? 假设我们有时间序列数据,这些数据来自一个(非线性)动态学系统。
识别一个系统意味着基于数据推断该系统的控制方程。换句话说,就是找到动态系统方…
推荐文章
- $.ajax #fm,【图片】95范加尔Ajax的荣光,95Ajax战术在FM的复刻。战术以及思想讨论【fm2017吧】_百度贴吧...
- (39)智能电池
- (delphi11最新学习资料) Object Pascal 学习笔记---第2章第五节(日期和时间)
- (golang)切片何时会创建新切片或影响原切片
- (vue)获取对象的键遍历,同时循环el-tab页展示key及内容
- (绝密内部培训)如何用CHAT GPT工具做好海外的TIKTOK?
- (开源)2023工训大赛智能垃圾分类项目(可循环播放视频,显示垃圾分类信息,拍照识别,垃圾分类,满载报警,压缩)
- (离散数学)命题及命题的真值
- (六)激光线扫描-三维重建
- (十)SpringCloud系列——openfeign的高级特性实战内容介绍
- (四)STM32 操作 GPIO 点亮 LED灯 / GPIO工作模式
- (五)关系数据库标准语言SQL











![[论文笔记]Are Large Language Models All You Need for Task-Oriented Dialogue?](https://img-blog.csdnimg.cn/img_convert/a9a583c33a94ba4467be7e9b1b88712b.png)