【数据结构】红黑树实现详解

在本篇博客中，作者将会带领你使用C++来实现一棵红黑树，此红黑树的实现是基于二叉搜索树和AVLTree一块来讲的，所以在看本篇博客之前，你可以先看看下面这两篇博客

【C++】二叉搜索树-CSDN博客

【数据结构】AVLTree实现详解-CSDN博客

在这棵红黑树中，我们用到了二叉搜索树的插入规则和AVLTree的旋转，所以在本篇博客中，在旋转部分可以直接看AVLTree的博客。

目录

一.什么是红黑树 

 1.红黑树的性质

二.红黑树的实现 

1.红黑树结点的定义

2.红黑树类的定义

3.红黑树的插入 

①按二叉搜索树的规则进行插入 

②判断红黑树的性质是否被破坏

③如果被破坏，则进行调整 

cur为红，cur_parent为红，grandparent为黑，uncle为红

cur为红，cur_parent为红，grandparent为黑，uncle为黑\uncle不存在

uncle不存在 

uncle存在且为黑

cur为红，cur_parent为红，grandparent为红，uncle为黑\uncle不存在 

uncle不存在

uncle存在且为黑 

④ 调整代码

⑤最终插入代码 

⑥代码分析

4.红黑树的查找

5.红黑树的修改 

三.测试

四.所有源代码

blog_RBTree.h

test.cpp 

一.什么是红黑树 

红黑树是一棵二叉搜索树，它的结点不是黑的就是红的，其中它有一个非常重要的特点：

通过对任何一条从根到叶子的路径上各个结点的着色控制，保证了红黑树没有一条路径会比最短路径长出两倍，达到接近平衡的特点。 

看到这句话，可能你还云里雾里的，但是不要怕，简单的来说，红黑树的特点就是：找出树中最短的路径和最长的路径，其中这条最长路径的长度不会大于最短路径长度的两倍。

如下图所示：

在这棵红黑树中，最短的路径是最左边的那条，长度为3，最长的路径是最右边的那条，长度为4，即4 < 2*3，最长的路径不会大于最短路径的两倍。

 1.红黑树的性质

那么红黑树是怎么做到上面的这个特点的呢？

那是因为红黑树需要遵循下面这5条性质：

1.每个结点不是红的就是黑的

2.根节点是黑色的

3.如果一个结点是红色的，那么它的两个孩子一定是黑色的

4.对于每个结点，从该结点到其所有后代叶结点的路径上，均包含相同数量的黑色结点

5.每个叶子结点都是黑色的（此处的我叶子结点指的是空结点）

对于这5条性质来说，可能有一些很难理解，但是不用怕，我们来解释一下。

对于1、2这两条性质来说，很好理解就字面意思，这里就不做过多的解释，其中最重要的是3、4这两条性质，在下面的红黑树插入讲解中，我们都将会围绕着3、4这两条性质来进行。

3.如果一个结点是红色的，那么它的两个孩子一定是黑色的。

        其实这个也很好理解，但是这个很重要。其规则如下图所示。

4.对于每个结点，从该结点到其所有后代叶结点的路径上，均包含相同数量的黑色结点。

         这条规则说的是，从任意一个结点开始，一直往下走，走遍所有可能，这其中会有很多条可能的路径，但是这些路径都有一个特点，就是每条路径上的黑色结点的个数相同。如下图所示。

5.每个叶子结点都是黑色的（这里的叶子结点指的是空结点），如下图所示。 但是其实这个并不是那么重要，理解就行了。

那么为什么只要遵循上面这五条性质，就能做到红黑树的特点的呢？红黑树的特点是，最长路径的长度不会大于最短路径的长度的两倍。

既然红黑树的特点与最短路径和最长路径有关，那么我们来把这两条路径分析一下。

最短路径：通过这五条性质，我们可以知道在一棵红黑树中，最短路径上，一定全是黑结点。不会再有情况比这种情况要短了。

最长路径： 对于最长路径来说，由于有性质4，所以在最长路径上，它的黑色结点的个数一定和最短路径的黑色结点个数相同。又由于有性质3，对于最长的路径来说，它一定是黑结点，红结点交替的。所以最长的路径的长度不会大于最短路径的两倍。

如下图所示

二.红黑树的实现 

知道了红黑树的性质和特点，接下来我们可以来实现一棵红黑树了。 

1.红黑树结点的定义

在定义红黑树的结点时，与普通的树结点不同的是，这里多了一个_parent指针和一个记录结点颜色的变量。 

	enum Color{BLACK,RED};template<class T>struct TreeNode{//成员变量T _data;//数据TreeNode<T>* _left;TreeNode<T>* _right;TreeNode<T>* _parent;Color _col;//保存结点的颜色//构造函数TreeNode(const T& data):_data(data),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//每生成一个新结点，都将结点的颜色默认给红色，至于为什么，后面会解释{}};

2.红黑树类的定义

对于红黑树类的定义，我们先简单的给出一个构造函数，并将_root根结点赋值为nullptr即可。 

	template<class T>class RBTree{typedef TreeNode<T> Node;public://构造函数RBTree():_root(nullptr)//给根结点一个nullptr{}private:Node* _root;};

3.红黑树的插入 

接下来就是最重要的部分了，红黑树的插入，对于红黑树的插入，我们可以分为两个过程： 

1.先按二叉搜索树的插入规则把新结点插入进去先。

2.插入新结点后，判断红黑树的性质有没有被破坏，如果没有被破坏，则插入直接结束，如果有被破坏，则进行调整处理。

由于插入结点的函数有点长，所以这里把插入函数分开来实现 。下面是函数的名称以及参数

bool insert(const T& data)

①按二叉搜索树的规则进行插入 

二叉搜索树的插入规则就是，先不管三七二十一，先把新结点插入进去再说。 

对于二叉搜索树的插入规则，这里不在多讲，不是很理解的，可以看下面这篇博客，这里面讲到了二叉搜索树的插入实现。我们在这里直接给出代码。

【C++】二叉搜索树-CSDN博客

			//如果树为NULL，则直接将新结点给到_rootif (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//把新结点给_root后，要记得把颜色给位BLACKreturn true;}Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr){if (data > cur->_data){cur_parent = cur;cur = cur->_right;}else if (data < cur->_data){cur_parent = cur;cur = cur->_left;}else//说明该值已经存在，不进行插入{return false;	}}//将新结点插入Node* newnode = new Node(data);if (cur_parent->_data > data){cur_parent->_left = cur;cur->_parent = cur_parent;}else{cur_parent->_right = cur;cur->_parent = cur_parent;}

②判断红黑树的性质是否被破坏

当插入完结点后，就要判断红黑树的性质是否被破坏，如没有，则插入结束，如果有，则进行调整处理。 

对于前者没有什么好讨论的，我们在着重于讨论后者。

红黑树的性质：

1.每个结点不是红的就是黑的

2.根节点是黑色的

3.如果一个结点是红色的，那么它的两个孩子一定是黑色的

4.对于每个结点，从该结点到其所有后代叶结点的路径上，均包含相同数量的黑色结点

5.每个叶子结点都是黑色的（此处的我叶子结点指的是空结点）

首先我们来思考一个问题，如果新增了一个结点，你希望这个新增的结点是红色的还是黑色的呢？

其实我们希望这个新增的结点是红色的，为什么，我们来从红黑树的性质来分析。

当我们新插入一个结点的时候，性质1、2、5是绝对不会被破坏的，这应该很好理解。

被破坏的只有3或者4，当我们插入一个红结点，有可能会破坏性质3，当我们插入一个黑结点，会破坏性质4，如下图所示。

既然不管插入的是红结点还是黑结点，都会破坏红黑树的性质，那么为什么我们要选择插入红结点呢？

其实大家凭感觉来判断，应该都会感觉性质3的破坏更好的调整，而性质4的破坏不好调整，因为对于性质4的破坏，我们去给其他路径新增黑结点显然不合理，所以只有给当前路径减少一个黑结点来解决，那么我们把这个新增的结点给成红色即可。

既然这里已经确定了新增的结点一定为红色，所以对于红黑树的调整，我们都围绕着这个来讲解。 

③如果被破坏，则进行调整 

对于性质3的破坏，我们可以分为下面着三种情况。 

cur为红，cur_parent为红，grandparent为黑，uncle为红

上图是其中的一种插入的情况，其中cur刚好是叶子，但是cur也有可能不是叶子，所以我们可以给出这种情况的抽象图。

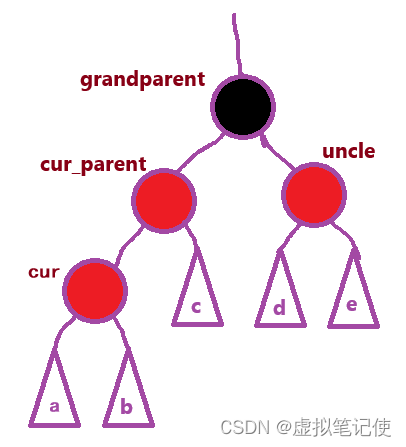
对于这种情况，我们的调整过程是这样的：

把cur_parent和uncle的颜色变为黑色，grandparent的颜色变为红色。如下图所示。

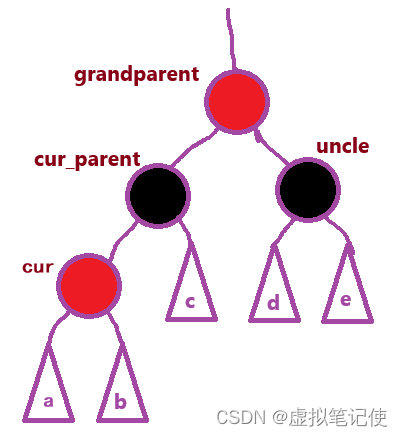
但是这样的处理后，还会有可能会发生性质破坏，例如grandparent的父结点还是红色，对于这样的情况，我们只需要把grandparent给cur，继续向上处理即可。如下图所示。  

cur为红，cur_parent为红，grandparent为黑，uncle为黑\uncle不存在

在这种情况中，又可以分为两种小情况，一种是uncle存在且为黑，一种是uncle不存在。

uncle不存在 

先来说说第一种情况，uncle不存在的情况，我们先来看图。 

对于这种情况来说，cur一定是新插入的结点，因为如果cur不是新插入的结点，那么说明是由情况一调整而来的，那么既然是从情况一调整而来的，那么cur的孩子肯定是黑色，但是这样就不符合性质4：从任意结点开始，每条路径的黑色结点的数量相同。 

uncle存在且为黑

接着第二种情况，uncle存在且为黑色，我们先来看图。 

对于这种情况来说，cur一定不是新插入的结点，因为如果cur是新插入的结点，那么在插入cur之前，这棵红黑树违反了性质4：从任意结点开始，每条路径的黑色结点的个数相同。 

基于这两种情况，我们可以给出这它们的抽象图，同时它们的调整方法是一样的。 

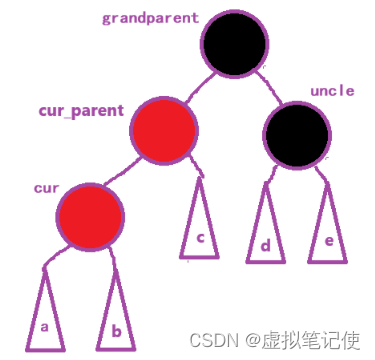
对于情况二，我们的处理是对grandparent进行一个右单旋，后调整cur_parent和grandparent的颜色即可。如下图所示。

 

cur为红，cur_parent为红，grandparent为红，uncle为黑\uncle不存在 

情况三看上去与情况二类似，其实可以说是，也可以说不是，首先同样的，情况三也可以分为两种情况，一种是uncle不存在，一种是uncle存在且为黑色。 

uncle不存在

我们直接来看图。

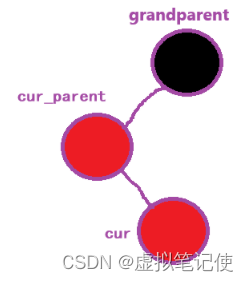
也情况二不同的是，它是一个折线。同样的如果uncle不存在，那么cur一定是新插入的结点。 

uncle存在且为黑 

同样的，我们直接来看图。 

对于这种情况来说，cur一定不是新插入的结点，它是由情况一调整过来的 

基于这两种情况，我们可以给出它的抽象图处理，如下图所示。  

对于情况三，我们的处理是，先对cur_parent进行一个左单旋，左单旋后，要交换cur和cur_parent，后再对grandparent进行一个右单旋，最后再调整颜色，如下图所示。

 

 

走到这里，我们所有的情况都已经讲完了，接下来可以编写我们的调整代码了。 

④ 调整代码

注意，我们上面讲到的三种情况没有覆盖到全部情况，因为还有另外三种情况是上面这三种情况的反方向，如情况一的反方向，如下图所示。 

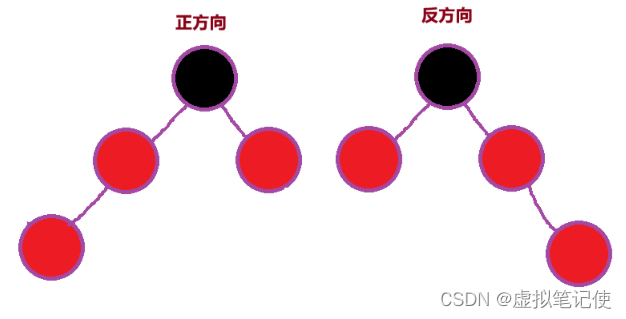
同样的情况二和情况三也有它们的反方向，这里就不在多讲了，逻辑都是一样的。接下来我们可以来编写我们的调整代码了，我们的调整代码可以分为如上图所示的正反向和反方向来编写。   

			//调整结点代码while (cur_parent != nullptr && cur_parent->_col == RED){Node* grandparent = cur_parent->_parent;if (grandparent->_left == cur_parent)//正方向{Node* uncle = grandparent->_right;if (uncle != nullptr && uncle->_col == RED)//情况一,uncle存在且为红{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;//继续向上处理cur = grandparent;cur_parent = cur->_parent;}else//情况二和情况三{//这里情况三经过第一次旋转后可以变成情况二，所以可以先判断是否是情况三if (cur_parent->_right == cur)//这种情况就是情况三{//先进行一个左单旋RotateL(cur_parent);swap(cur, cur_parent);//这里一定要进行交换，不然如果是情况二的，会出现逻辑错误}//代码走到这里就一定是情况二了RotateR(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}else if (grandparent->_right == cur_parent)//反方向{Node* uncle = grandparent->_left;if (uncle != nullptr && uncle->_col == RED)//反方向的情况一{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;cur_parent = cur->_parent;}else//反方向的情况二和情况三{if (cur_parent->_left == cur){RotateR(cur_parent);swap(cur, cur_parent);}RotateL(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}}_root->_col = BLACK;

⑤最终插入代码 

		//插入结点bool insert(const T& data){//如果树为NULL，则直接将新结点给到_rootif (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//把新结点给_root后，要记得把颜色给位BLACKreturn true;}Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr){if (data > cur->_data){cur_parent = cur;cur = cur->_right;}else if (data < cur->_data){cur_parent = cur;cur = cur->_left;}else//说明该值已经存在，不进行插入{return false;	}}//将新结点插入cur = new Node(data);if (cur_parent->_data > data){cur_parent->_left = cur;cur->_parent = cur_parent;}else{cur_parent->_right = cur;cur->_parent = cur_parent;}//调整结点代码while (cur_parent != nullptr && cur_parent->_col == RED){Node* grandparent = cur_parent->_parent;if (grandparent->_left == cur_parent)//正方向{Node* uncle = grandparent->_right;if (uncle != nullptr && uncle->_col == RED)//情况一,uncle存在且为红{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;//继续向上处理cur = grandparent;cur_parent = cur->_parent;}else//情况二和情况三{//这里情况三经过第一次旋转后可以变成情况二，所以可以先判断是否是情况三if (cur_parent->_right == cur)//这种情况就是情况三{//先进行一个左单旋RotateL(cur_parent);swap(cur, cur_parent);}//代码走到这里就一定是情况二了RotateR(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}else if (grandparent->_right == cur_parent)//反方向{Node* uncle = grandparent->_left;if (uncle != nullptr && uncle->_col == RED)//反方向的情况一{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;cur_parent = cur->_parent;}else//反方向的情况二和情况三{if (cur_parent->_left == cur){RotateR(cur_parent);swap(cur, cur_parent);}RotateL(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}}_root->_col = BLACK;}

⑥代码分析

在我们的插入函数的调整部分中，有下面这段逻辑

			//调整结点代码while (cur_parent != nullptr && cur_parent->_col == RED){Node* grandparent = cur_parent->_parent;if (grandparent->_left == cur_parent)//正方向{}

有的人可能会有个疑问，就是在这里的grandparent指针中，没有进行做判空处理，不会出现grandparent是个空指针的错误吗？

答案是不会的，原因如下： 

首先我们可以确定的是，cur和cur_parent指针不会是空指针，不然这个while循环也不会进入，且进去这个循环后，cur和cur_parent结点的颜色一定为红色。那么既然cur_parent为红色，那么cur_parent就一定不是根结点，因为在红黑树的性质中，根结点一定是黑色的，但是这个时候cur_parent是红色的，说明cur_parent一定有父结点，所以不会出现grandparent为空指针的情况。

4.红黑树的查找

红黑树的查找就比较简单了，就是普通的二叉搜索树的查找方式，这里就不在多解释，不了解的可以去看前面的二叉搜索树的博客。 

//查找结点Node* find(const T& data){Node* cur = _root;if (data > cur->_data){cur = cur->_right;}else if (data < cur->_data){cur = cur->_left;}else{return cur;}return nullptr;}

5.红黑树的修改 

不是所有红黑树的结点都是可以修改的，只有<key,value>模型的红黑树才能修改，例如STL中的map，而key模型的红黑树是不能修改的，例如STL中的set，我们这里默认实现的是key模型的红黑树，所以在这里是不能修改的，但是如果想要做到修改，可以把这棵红黑树改成<key,value>模型即可，即在TreeNode结构体中，多加一个参数即可。 

三.测试

看到这里，我们的这棵红黑树除了删除都已经搞定了，那么我们如果判断我们写的代码是对的呢？即我们写的这棵红黑树到底是不是红黑树，判断这棵树是不是红黑树的方法就是用红黑树的性质去检查它即可。 

首先，我们再来看一下红黑树的五条性质： 

1.每个结点不是红的就是黑的

2.根节点是黑色的

3.如果一个结点是红色的，那么它的两个孩子一定是黑色的

4.对于每个结点，从该结点到其所有后代叶结点的路径上，均包含相同数量的黑色结点

5.每个叶子结点都是黑色的（此处的我叶子结点指的是空结点） 

通过下面这个代码，可以测试一个红黑树是否正确。 

		//判断是否符合红黑树的性质bool JudgeTree(){//空树也是红黑树if (_root == nullptr){return true;}//性质1：树结点不是红的就是黑的//这条性质就没必要检查的了//性质2：根结点一定是黑色的if (_root->_col != BLACK){cout << "违反性质2：根结点一定是黑色的" << endl;return false;}//性质5:所有叶子结点都是黑色的//这个性质也没必要检查size_t blackcount = 0;Node* cur = _root;while (cur != nullptr)//先求出一条路径中的黑色结点的个数{if (cur->_col == BLACK){blackcount++;}cur = cur->_left;}size_t k = 0;//用来存储黑色结点的个数return _JudgeTree(_root, k, blackcount);//判断性质3和性质4//性质3：如果一个结点是红色的，那么它的孩子一定是黑色的//性质4：每条路径上的黑色结点的个数都相同}//判断是否红黑树的子函数bool _JudgeTree(Node* root, size_t k, size_t blackcount){//当root走到NULL的时候，判断这条路径的黑色结点个数是否==blackcountif (root == nullptr){if (k == blackcount){return true;}else{cout << "违反性质4：每条路径上的黑结点个数相同" << endl;return false;}			}//如果结点是红色的，判断它的父结点是否也为红色Node* root_parent = root->_parent;if (root_parent != nullptr && root->_col == RED){if (root_parent->_col == RED){cout << "违反性质3：如果一个结点是红色的，那么它的孩子一定是黑色的" << endl;return false;}}//如果结点是黑色的，则k++if (root->_col == BLACK){k++;}return _JudgeTree(root->_left, k, blackcount) && _JudgeTree(root->_right, k, blackcount);}

四.所有源代码

blog_RBTree.h

#pragma once
#include<iostream>
#include<time.h>
using namespace std;
namespace blog_RBTree
{enum Color{BLACK,RED};template<class T>struct TreeNode{//成员变量T _data;//数据TreeNode<T>* _left;TreeNode<T>* _right;TreeNode<T>* _parent;Color _col;//保存结点的颜色//构造函数TreeNode(const T& data):_data(data),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//每生成一个新结点，都将结点的颜色默认给红色，至于为什么，后面会解释{}};template<class T>class RBTree{typedef TreeNode<T> Node;public://构造函数RBTree():_root(nullptr)//给根结点一个nullptr{}//插入结点bool insert(const T& data){//如果树为NULL，则直接将新结点给到_rootif (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//把新结点给_root后，要记得把颜色给位BLACKreturn true;}Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr){if (data > cur->_data){cur_parent = cur;cur = cur->_right;}else if (data < cur->_data){cur_parent = cur;cur = cur->_left;}else//说明该值已经存在，不进行插入{return false;	}}//将新结点插入cur = new Node(data);if (cur_parent->_data > data){cur_parent->_left = cur;cur->_parent = cur_parent;}else{cur_parent->_right = cur;cur->_parent = cur_parent;}//调整结点代码while (cur_parent != nullptr && cur_parent->_col == RED){Node* grandparent = cur_parent->_parent;if (grandparent->_left == cur_parent)//正方向{Node* uncle = grandparent->_right;if (uncle != nullptr && uncle->_col == RED)//情况一,uncle存在且为红{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;//继续向上处理cur = grandparent;cur_parent = cur->_parent;}else//情况二和情况三{//这里情况三经过第一次旋转后可以变成情况二，所以可以先判断是否是情况三if (cur_parent->_right == cur)//这种情况就是情况三{//先进行一个左单旋RotateL(cur_parent);swap(cur, cur_parent);}//代码走到这里就一定是情况二了RotateR(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}else if (grandparent->_right == cur_parent)//反方向{Node* uncle = grandparent->_left;if (uncle != nullptr && uncle->_col == RED)//反方向的情况一{cur_parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;cur_parent = cur->_parent;}else//反方向的情况二和情况三{if (cur_parent->_left == cur){RotateR(cur_parent);swap(cur, cur_parent);}RotateL(grandparent);cur_parent->_col = BLACK;grandparent->_col = RED;break;}}}_root->_col = BLACK;}//查找结点Node* find(const T& data){Node* cur = _root;if (data > cur->_data){cur = cur->_right;}else if (data < cur->_data){cur = cur->_left;}else{return cur;}return nullptr;}//判断是否符合红黑树的性质bool JudgeTree(){//空树也是红黑树if (_root == nullptr){return true;}//性质1：树结点不是红的就是黑的//这条性质就没必要检查的了//性质2：根结点一定是黑色的if (_root->_col != BLACK){cout << "违反性质2：根结点一定是黑色的" << endl;return false;}//性质5:所有叶子结点都是黑色的//这个性质也没必要检查size_t blackcount = 0;Node* cur = _root;while (cur != nullptr)//先求出一条路径中的黑色结点的个数{if (cur->_col == BLACK){blackcount++;}cur = cur->_left;}size_t k = 0;//用来存储黑色结点的个数return _JudgeTree(_root, k, blackcount);//判断性质3和性质4//性质3：如果一个结点是红色的，那么它的孩子一定是黑色的//性质4：每条路径上的黑色结点的个数都相同}private://左单旋	void RotateL(Node* cur_parent){Node* cur = cur_parent->_right;Node* cur_left = cur->_left;//改变指针的链接关系cur_parent->_right = cur_left;if (cur_left != nullptr){cur_left->_parent = cur_parent;}cur->_left = cur_parent;Node* cur_parent_parent = cur_parent->_parent;cur_parent->_parent = cur;//旋转完成后要判断cur_parent是否为根if (cur_parent_parent != nullptr)//说明cur_parent不是根{if (cur_parent_parent->_data < cur_parent->_data){cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}}else//说明cur_parent是根{_root = cur;cur->_parent = nullptr;}}//右单旋void RotateR(Node* cur_parent){Node* cur = cur_parent->_left;Node* cur_right = cur->_right;cur_parent->_left = cur_right;if (cur_right != nullptr){cur_right->_parent = cur_parent;}cur->_right = cur_parent;Node* cur_parent_parent = cur_parent->_parent;cur_parent->_parent = cur;if (cur_parent_parent != nullptr){if (cur_parent_parent->_data > cur_parent->_data){cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}}else{_root = cur;cur->_parent = nullptr;}}//获取根节点Node* GetRoot(){return _root;}//判断是否红黑树的子函数bool _JudgeTree(Node* root, size_t k, size_t blackcount){//当root走到NULL的时候，判断这条路径的黑色结点个数是否==blackcountif (root == nullptr){if (k == blackcount){return true;}else{cout << "违反性质4：每条路径上的黑结点个数相同" << endl;return false;}}//如果结点是红色的，判断它的父结点是否也为红色Node* root_parent = root->_parent;if (root_parent != nullptr && root->_col == RED){if (root_parent->_col == RED){cout << "违反性质3：如果一个结点是红色的，那么它的孩子一定是黑色的" << endl;return false;}}//如果结点是黑色的，则k++if (root->_col == BLACK){k++;}return _JudgeTree(root->_left, k, blackcount) && _JudgeTree(root->_right, k, blackcount);}private:Node* _root;};void Test1(){srand(time(0));RBTree<int> root;const int n = 10000;for (int i = 0; i < n; i++){int input = rand();root.insert(input);}cout << root.JudgeTree() << endl;}
}

test.cpp  

#include"blog_RBTree.h"int main()
{blog_RBTree::Test1();return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/354957.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

使用opencv合并两个图像

使用opencv合并两个图像

本节的目的 linear blending&#xff08;线性混合&#xff09;使用**addWeighted()**来添加两个图像 原理 (其实我也没太懂&#xff0c;留个坑&#xff0c;感觉本科的时候线代没学好。不对&#xff0c;我本科就没学线代。) 源码分析 源码链接 #include "opencv2/imgc…
阅读更多...
spark学习总结

spark学习总结

系列文章目录 第1天总结&#xff1a;spark基础学习 1- Spark基本介绍&#xff08;了解&#xff09;2- Spark入门案例&#xff08;掌握&#xff09;3- 常见面试题&#xff08;掌握&#xff09; 文章目录 系列文章目录前言一、Spark基本介绍1、Spark是什么1.1 定义1.2 Spark与M…
阅读更多...
从0进入微服务需要了解的基础知识

从0进入微服务需要了解的基础知识

文章目录 系统架构演化过程为什么要了解系统架构的演化过程技术发展认知技术选型与创新 演变过程单体架构分层-分布式集群微服务 分布式\集群\微服务 微服务中的核心要素-拆分原则项目拆分与复杂度微服务的拆分维度有哪些小结 微服务中的核心要素服务化进行拆分后一定是微服务&…
阅读更多...
Unity和UE免费领恐怖书本头怪兽角色模型恐怖或奇幻游戏monster适合FPS类型PBR202406202143

Unity和UE免费领恐怖书本头怪兽角色模型恐怖或奇幻游戏monster适合FPS类型PBR202406202143

Unity和UE免费领恐怖书本头怪兽角色模型恐怖或奇幻游戏monster适合FPS类型PBR202406202143 Unity恐怖书本头怪兽角色模型&#xff1a;https://prf.hn/l/zpBqgVl UE恐怖书本头怪兽角色模型&#xff1a;https://prf.hn/l/4PzY1Qy 作者其他资产&#xff1a;https://prf.hn/l/0…
阅读更多...
百万级 QPS 接入层网关架构方案演进

百万级 QPS 接入层网关架构方案演进

文章目录 前言1、单机架构2、DNS 轮询3、Nginx 单机4、Nginx 主备 Keepalived5、LVS 主备 Keepalived Nginx 集群6、LVS 主备 Keepalived Nginx 集群 DNS 轮询 前言 随着PC、移动互联网的快速发展&#xff0c;越来越多的人通过手机、电脑、平板等设备访问各种各样APP、网…
阅读更多...
OCC介绍及框架分析

OCC介绍及框架分析

1.OCC介绍 Open CASCADE &#xff08;简称OCC&#xff09;是一开源的几何造型引擎&#xff0c;OCCT库是由Open CASCADE公司开发和市场运作的。它是为开源社区比较成熟的基于BREP结构的建模引擎&#xff0c;能够满足二维三维实体造型和曲面造型&#xff0c;国内研究和使用它的单…
阅读更多...
[论文笔记]Are Large Language Models All You Need for Task-Oriented Dialogue?

[论文笔记]Are Large Language Models All You Need for Task-Oriented Dialogue?

引言 今天带来论文Are Large Language Models All You Need for Task-Oriented Dialogue?的笔记。 主要评估了LLM在完成多轮对话任务以及同外部数据库进行交互的能力。在明确的信念状态跟踪方面&#xff0c;LLMs的表现不及专门的任务特定模型。然而&#xff0c;如果为它们提…
阅读更多...
【机器学习】基于稀疏识别方法的洛伦兹混沌系统预测

【机器学习】基于稀疏识别方法的洛伦兹混沌系统预测

1. 引言 1.1. DNN模型的来由 从数据中识别非线性动态学意味着什么&#xff1f; 假设我们有时间序列数据&#xff0c;这些数据来自一个&#xff08;非线性&#xff09;动态学系统。 识别一个系统意味着基于数据推断该系统的控制方程。换句话说&#xff0c;就是找到动态系统方…
阅读更多...
[创业之路-120] ：全程图解：软件研发人员如何从企业的顶层看软件产品研发？

[创业之路-120] ：全程图解：软件研发人员如何从企业的顶层看软件产品研发？

目录 一、企业全局 二、供应链 三、团队管理 四、研发流程IPD 五、软件开发流程 六、项目管理 七、研发管理者的自我修炼 一、企业全局 二、供应链 三、团队管理 四、研发流程IPD 五、软件开发流程 六、项目管理 七、研发管理者的自我修炼
阅读更多...
系统架构设计师 - 数据库系统(1)

系统架构设计师 - 数据库系统(1)

数据库系统 数据库系统数据库模式 ★分布式数据库 ★★★数据库设计阶段 ★★ER模型 ★关系模型 ★ ★结构约束条件完整性约束 关系代数 ★ ★ ★ ★概述自然连接 大家好呀&#xff01;我是小笙&#xff0c;本章我主要分享系统架构设计师 - 数据库系统(1)知识&#xff0c;希望内…
阅读更多...
idea插件开发之在项目右键添加菜单

idea插件开发之在项目右键添加菜单

写在前面 本文看下如何在右键列表中增加菜单。 正戏 首先创建一个Action&#xff0c;要显示的menu选择ProjectViewPopupMenu&#xff0c;如下&#xff1a; action public class CAction extends AnAction {Overridepublic void actionPerformed(AnActionEvent e) { // …
阅读更多...
OSPF 动态路由协议（思科、华为）

OSPF 动态路由协议（思科、华为）

#交换设备 OSPF 动态路由协议 一、基本概念 1.中文翻译&#xff1a;开放式最短路径优先路由协议&#xff08;open shortest path first&#xff09;&#xff0c;是一个内部网关路由协议&#xff08;一个自治系统内&#xff09;2.也称为&#xff1a;链路状态路由协议&#xf…
阅读更多...
火爆全网 LLM大模型教程：从零开始构建大语言模型，git突破18K标星

火爆全网 LLM大模型教程：从零开始构建大语言模型，git突破18K标星

什么&#xff01;一本书的Github仓库居然有18.5k的星标&#xff01;&#xff08;这含金量不必多说&#xff09; 对GPT大模型感兴趣的有福了&#xff01;这本书的名字叫 《Build a Large Language Model (From Scratch)》 也就是 从零开始构建大语言模型&#xff01; 虽然这是一…
阅读更多...
常说的云VR是什么意思？与传统vr的区别

常说的云VR是什么意思？与传统vr的区别

虚拟现实&#xff08;Virtual Reality&#xff0c;简称VR&#xff09;是一种利用计算机技术模拟产生一个三维空间的虚拟世界&#xff0c;让用户通过视觉、听觉、触觉等感官&#xff0c;获得与现实世界类似或超越的体验。VR技术发展历程可追溯至上世纪&#xff0c;经历概念提出、…
阅读更多...
鸿蒙 Web组件的生命周期（api10、11、12）

鸿蒙 Web组件的生命周期（api10、11、12）

概述 开发者可以使用Web组件加载本地或者在线网页。 Web组件提供了丰富的组件生命周期回调接口&#xff0c;通过这些回调接口&#xff0c;开发者可以感知Web组件的生命周期状态变化&#xff0c;进行相关的业务处理。 Web组件的状态主要包括&#xff1a;Controller绑定到Web组…
阅读更多...
两行css 实现瀑布流

两行css 实现瀑布流

html <ul ><li><a href"" ><img src"05094532gc6w.jpg" alt"111" /><p>传奇</p></a></li><li><a href"" ><img src"05094532gc6w.jpg" alt"111"…
阅读更多...
文件防篡改监控工具 - WGCLOUD全面介绍

文件防篡改监控工具 - WGCLOUD全面介绍

WGCLOUD是一款优秀的运维监控软件&#xff0c;免费、轻量、高效&#xff0c;部署容易&#xff0c;上手简单&#xff0c;对新手非常友好 WGCLOUD部署完成后&#xff0c;点击菜单【文件防篡改】&#xff0c;可以看到如下页面 我们点击【添加】按钮&#xff0c;输入监控文件的信息…
阅读更多...
深圳比创达EMC｜EMC与EMI测试整改：保障电子设备电磁兼容性步骤

深圳比创达EMC｜EMC与EMI测试整改：保障电子设备电磁兼容性步骤

随着电子技术的迅猛发展&#xff0c;电子设备在我们的日常生活中扮演着越来越重要的角色。然而&#xff0c;这些设备在运行时产生的电磁干扰&#xff08;EMI&#xff09;以及对外界电磁干扰的敏感性&#xff08;EMC&#xff09;问题&#xff0c;不仅影响着设备本身的性能&#…
阅读更多...
Windows电脑部署Jellyfin服务端并进行远程访问配置详细教程

Windows电脑部署Jellyfin服务端并进行远程访问配置详细教程

文章目录 前言1. Jellyfin服务网站搭建1.1 Jellyfin下载和安装1.2 Jellyfin网页测试 2.本地网页发布2.1 cpolar的安装和注册2.2 Cpolar云端设置2.3 Cpolar本地设置 3.公网访问测试4. 结语 前言 本文主要分享如何使用Windows电脑本地部署Jellyfin影音服务并结合cpolar内网穿透工…
阅读更多...
代理模式（静态代理/动态代理）

代理模式（静态代理/动态代理）

代理模式&#xff08;Proxy Pattern&#xff09; 一 定义 为其他对象提供一种代理&#xff0c;以控制对这个对象的访问。 代理对象在客户端和目标对象之间起到了中介作用&#xff0c;起到保护或增强目标对象的作用。 属于结构型设计模式。 代理模式分为静态代理和动态代理。…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023