torch.nn.GELU 模块在 PyTorch 中实现了高斯误差线性单元(GELU)激活函数。GELU 被用于许多深度学习模型中,包括Transformer,因为它相比传统的 ReLU(整流线性单元)函数能够更好地近似神经元的真实激活行为。
概述
- 功能: 应用 GELU 激活函数。
- 公式: GELU 激活函数可以表示为:
GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) GELU(x)=x⋅Φ(x)
其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的累积分布函数。
使用方法
要在神经网络中使用 torch.nn.GELU 模块,你可以简单地导入它并将其添加到模型的层中。以下是一个示例:
import torch
import torch.nn as nnclass MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()self.layer1 = nn.Linear(10, 20)self.gelu = nn.GELU()self.layer2 = nn.Linear(20, 10)def forward(self, x):x = self.layer1(x)x = self.gelu(x)x = self.layer2(x)return x# 创建模型实例
model = MyModel()# 创建一个随机输入张量
input_tensor = torch.randn(5, 10)# 前向传播
output_tensor = model(input_tensor)
print(output_tensor)
解释
nn.Linear(10, 20): 一个线性层,输入大小为 10,输出大小为 20。nn.GELU(): GELU 激活函数,应用于第一个线性层的输出。nn.Linear(20, 10): 另一个线性层,输入大小为 20,输出大小为 10。
GELU 激活函数用于在模型中引入非线性,这有助于模型学习更复杂的模式。
GELU 的优点
- 平滑近似: GELU 提供了一种比 ReLU 更平滑的神经元激活近似,这可以帮助训练的稳定性和收敛性。
- 概率解释: 通过结合累积分布函数,GELU 以更有原则的方式考虑激活的概率,这可能在某些模型(尤其是自然语言处理 (NLP) 和计算机视觉 (CV) 中)带来更好的性能。
通过在你的 PyTorch 模型中使用 torch.nn.GELU,你可以利用这些优点来提高神经网络的性能和训练动态。
GELU(Gaussian Error Linear Unit)激活函数是在论文《Gaussian Error Linear Units (GELUs)》中提出的。这篇论文由 Dan Hendrycks 和 Kevin Gimpel 于 2016 年发表。
以下是使用 Python 和 Matplotlib 绘制 GELU 激活函数的函数曲线的代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf# 定义 GELU 激活函数
def gelu(x):return 0.5 * x * (1 + erf(x / np.sqrt(2)))# 生成 x 轴数据
x = np.linspace(-3, 3, 400)
# 计算 y 轴数据
y = gelu(x)# 绘制 GELU 激活函数曲线
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='GELU', color='blue')
plt.title('GELU Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.show()
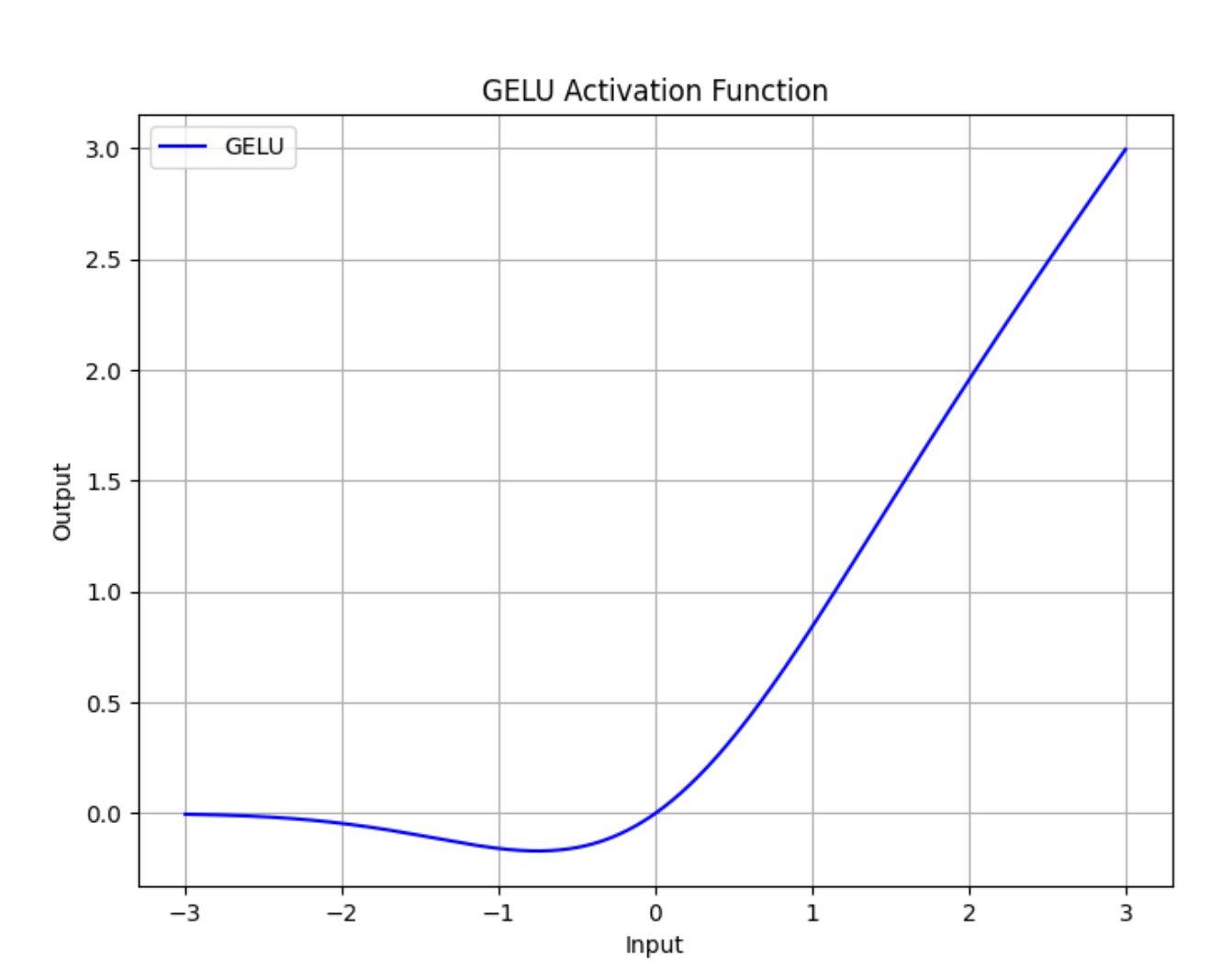
运行上述代码将生成一个展示 GELU 激活函数的曲线图:
优点:
- 平滑的近似:
GELU 提供了比 ReLU 更平滑的激活函数,这有助于神经网络更稳定地训练并提高收敛性。ReLU 在负数区间完全关闭,而 GELU 会根据输入值的大小逐渐激活神经元。
- 概率解释:
GELU 将标准正态分布的累积分布函数(CDF)结合到激活函数中,以一种更有原则的方式处理激活的概率。这种方法考虑了输入值的分布,使得神经网络可以更有效地处理不同范围的输入。
- 更好的性能:
由于 GELU 函数的平滑性和概率解释,它在处理某些任务时(尤其是在自然语言处理 (NLP) 和计算机视觉 (CV) 任务中)表现出色。在这些任务中,GELU 激活函数可以提高模型的性能。
- 渐进式变化:
相对于 ReLU 的硬边界(即大于零输出本身,小于零输出零),GELU 提供了一种更加渐进式的激活方式,使得小负值输入仍然能够产生一定的激活效果,这在某些情况下可以提高模型的表现。
GELU 反向传播的公式
GELU 激活函数的公式
GELU 激活函数定义为:
GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) GELU(x)=x⋅Φ(x)
其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的累积分布函数。 Φ ( x ) \Phi(x) Φ(x) 的表达式为:
Φ ( x ) = 1 2 ( 1 + erf ( x 2 ) ) \Phi(x) = \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) Φ(x)=21(1+erf(2x))
GELU 的梯度公式
为了求 GELU 的梯度,我们需要对其进行求导。这里 erf ( x ) \text{erf}(x) erf(x) 是误差函数,定义为:
erf ( x ) = 2 π ∫ 0 x e − t 2 d t \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt erf(x)=π2∫0xe−t2dt
求导过程
GELU 的导数可以表示为:
d d x GELU ( x ) = d d x ( x ⋅ Φ ( x ) ) \frac{d}{dx} \text{GELU}(x) = \frac{d}{dx} \left( x \cdot \Phi(x) \right) dxdGELU(x)=dxd(x⋅Φ(x))
根据乘积法则:
d d x ( x ⋅ Φ ( x ) ) = Φ ( x ) + x ⋅ d d x Φ ( x ) \frac{d}{dx} \left( x \cdot \Phi(x) \right) = \Phi(x) + x \cdot \frac{d}{dx} \Phi(x) dxd(x⋅Φ(x))=Φ(x)+x⋅dxdΦ(x)
我们需要对 Φ ( x ) \Phi(x) Φ(x) 进行求导:
d d x Φ ( x ) = d d x ( 1 2 ( 1 + erf ( x 2 ) ) ) \frac{d}{dx} \Phi(x) = \frac{d}{dx} \left( \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) \right) dxdΦ(x)=dxd(21(1+erf(2x)))
由于常数部分导数为零,我们仅对 erf ( x 2 ) \text{erf}\left( \frac{x}{\sqrt{2}} \right) erf(2x) 进行求导:
d d x erf ( x 2 ) = 2 π e − ( x 2 ) 2 ⋅ 1 2 = e − x 2 / 2 2 π \frac{d}{dx} \text{erf}\left( \frac{x}{\sqrt{2}} \right) = \frac{2}{\sqrt{\pi}} e^{-\left( \frac{x}{\sqrt{2}} \right)^2} \cdot \frac{1}{\sqrt{2}} = \frac{e^{-x^2/2}}{\sqrt{2\pi}} dxderf(2x)=π2e−(2x)2⋅21=2πe−x2/2
所以:
d d x Φ ( x ) = 1 2 π e − x 2 / 2 \frac{d}{dx} \Phi(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdΦ(x)=2π1e−x2/2
将其代入前面的公式,我们得到:
d d x GELU ( x ) = Φ ( x ) + x ⋅ 1 2 π e − x 2 / 2 \frac{d}{dx} \text{GELU}(x) = \Phi(x) + x \cdot \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdGELU(x)=Φ(x)+x⋅2π1e−x2/2
因此,GELU 的梯度为:
d d x GELU ( x ) = 1 2 ( 1 + erf ( x 2 ) ) + x ⋅ 1 2 π e − x 2 / 2 \frac{d}{dx} \text{GELU}(x) = \frac{1}{2} \left( 1 + \text{erf}\left( \frac{x}{\sqrt{2}} \right) \right) + x \cdot \frac{1}{\sqrt{2\pi}} e^{-x^2/2} dxdGELU(x)=21(1+erf(2x))+x⋅2π1e−x2/2
Python 代码绘制 GELU 梯度曲线
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf, erfc# 定义 GELU 激活函数
def gelu(x):return 0.5 * x * (1 + erf(x / np.sqrt(2)))# 定义 GELU 激活函数的导数
def gelu_derivative(x):return 0.5 * (1 + erf(x / np.sqrt(2))) + (x * np.exp(-x**2 / 2)) / np.sqrt(2 * np.pi)# 生成 x 轴数据
x = np.linspace(-3, 3, 400)
# 计算 y 轴数据
y = gelu(x)
# 计算 y' 轴数据
dy = gelu_derivative(x)# 绘制 GELU 激活函数和梯度曲线
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='GELU', color='blue')
plt.plot(x, dy, label='GELU Derivative', color='red', linestyle='dashed')
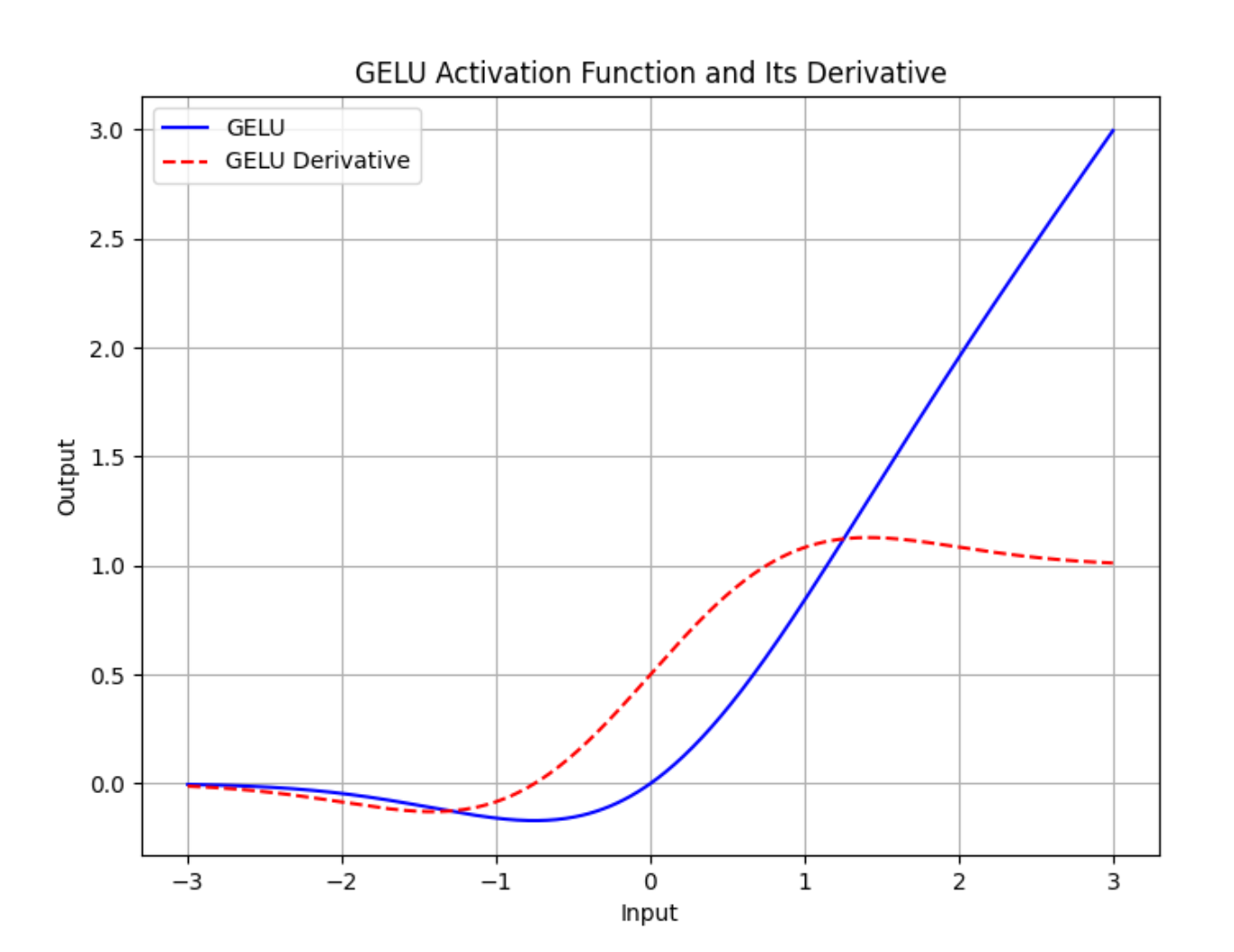
plt.title('GELU Activation Function and Its Derivative')
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.show()
运行这段代码将生成一个展示 GELU 激活函数及其梯度的曲线图,有助于直观地理解 GELU 在反向传播中的行为: