1. 移动零
- 题目描述
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。 - 解题思路
双指针遍历一遍即可解决:- 我们定义了两个指针 i 和 j,它们都初始化为 0。然后,我们开始遍历列表。j 指针用于遍历整个列表,而 i 指针用于跟踪下一个非零元素应该放置的位置。
- 在第一遍循环结束后,所有非零元素都已经按原始顺序排列在列表的前面。在第二遍循环中,我们将列表中剩余的所有位置都赋值为 0。
- 时间复杂度: O(n) 空间复杂度: O(1)
- 代码
class Solution:def moveZeroes(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""n = len(nums)if n == 0:returni = j = 0while j < n:if nums[j] != 0:nums[i] = nums[j]i += 1j += 1while i < n:nums[i] = 0i += 1
2. 盛最多水的容器
-
题目描述
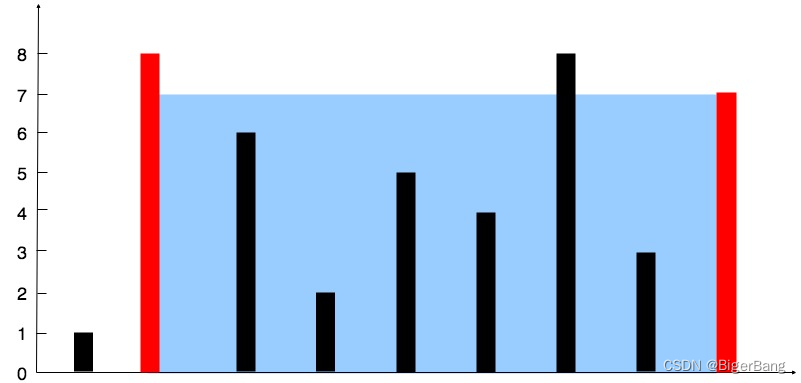
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
-
解题思路
- 我们初始化两个指针 l 和 r,分别指向数组的开始和结束位置,当前水容量是(r - l) * min(heights[l], heights[r]);
- 我们每次移动高度较小的指针,因为移动高度较大的指针不会增加水容量,只会减少水容量;比如如果heights[l] 较小,那么无论 r 指针如何移动,都不可能得到更大的水容量,因此我们选择移动 l 指针。
- 时间复杂度:O(n) 空间复杂度:O(1)
-
代码
class Solution:def maxArea(self, height: List[int]) -> int:n = len(height)if n == 0:return 0l, r = 0, n - 1res = 0while l < r:res = max(res, (r - l) * min(height[l], height[r]))if height[l] < height[r]:l += 1else:r -= 1return res
3. 三数之和
-
题目描述
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
-
解题思路
- 求解两数之和可以使用双指针,但此时需要先对数组进行排序,然后使用双指针分别指向数组的头部和尾部,然后根据两个指针指向的元素之和与目标值的大小关系来移动指针。
- 那么3数之和就可以在外面加上一层循环,循环内部使用双指针求两数之和等于traget - nums[i]。
- 在此过程中注意去重,包括外循环的去重和内循环的去重,如果当前元素和前一个元素相同,那么直接跳过。
- 时间复杂度:O(n^2) 空间复杂度:O(1)
-
代码
class Solution:def threeSum(self, nums: List[int]) -> List[List[int]]:n = len(nums)if n < 3:return []nums.sort()res = []for i in range(n-2):if i > 0 and nums[i] == nums[i - 1]:continuel, r = i + 1, n - 1while l < r:if nums[l] + nums[r] == 0 - nums[i]:res.append([nums[i], nums[l], nums[r]])l += 1r -= 1while l < r and nums[l] == nums[l - 1]:l += 1while l < r and nums[r] == nums[r + 1]:r -= 1elif nums[l] + nums[r] > 0 - nums[i]:r -= 1else:l += 1return res
4. 接雨水
-
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
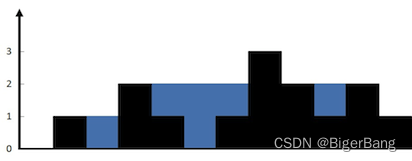
-
解题思路
- 总的接雨水量等于每个柱子上的接雨水量之和,每个柱子上的接雨水量等于左边最高柱子和右边最高柱子中较小的那个减去当前柱子的高度。
- 因此通过动态规划可以求解左边最高柱子和右边最高柱子,然后求解每个柱子上的接雨水量。
- 时间复杂度:O(n) 空间复杂度:O(n)
-
代码
class Solution:def trap(self, height: List[int]) -> int:n = len(height)if n < 3:return 0left_max = [0] * nright_max = [0] * nfor i in range(1, n):left_max[i] = max(left_max[i - 1], height[i - 1])for i in range(n - 2, -1, -1):right_max[i] = max(right_max[i + 1], height[i + 1])res = 0for i in range(n):if min(left_max[i], right_max[i]) > height[i]:res += min(left_max[i], right_max[i]) - height[i]return res
5. 总结
双指针在以下场景可以发挥作用:1. 原地对数组进行一些数据交换的操作,比如移动零、翻转数组、旋转数组等操作;2. 排序数组中求两数的目标和,比如三数之和题目;3.序列搜索中,从left = 0和right = n-1分别出发,可通过一定的规律先后移动left和right,最后再O(n)时间内完成搜索。