前言
我们在前面学习了使用数组来实现二叉树,但是数组实现二叉树仅适用于完全二叉树(非完全二叉树会有空间浪费),所以我们本章讲解的是链式二叉树,但由于学习二叉树的操作需要有一颗树,才能学习相关的基本操作,由于这只是开头,为了降低学习的成本,所以我们手动的来创建一颗普通的二叉树,等到本文的后面,再讲解真正的创建
二叉树的基本结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;创建新结点
BTNode*BuyNode(BTDataType x)
{BTNode* Node = (BTNode*)malloc(sizeof(BTNode));if (Node == NULL){perror("malloc fail:");exit(1);}Node->_data = x;Node->_left = Node->_right = NULL;
}创造树
BTNode* CreateBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);BTNode* node8 = BuyNode(8);node1->_left = node2;node2->_left = node3;node3->_right = node4;node1->_right = node5;node5->_right = node6;node6->_left = node7;node6->_right = node8;return node1;
}int main()
{BTNode* root = CreateBinaryTree();return 0;
}
最后效果如图
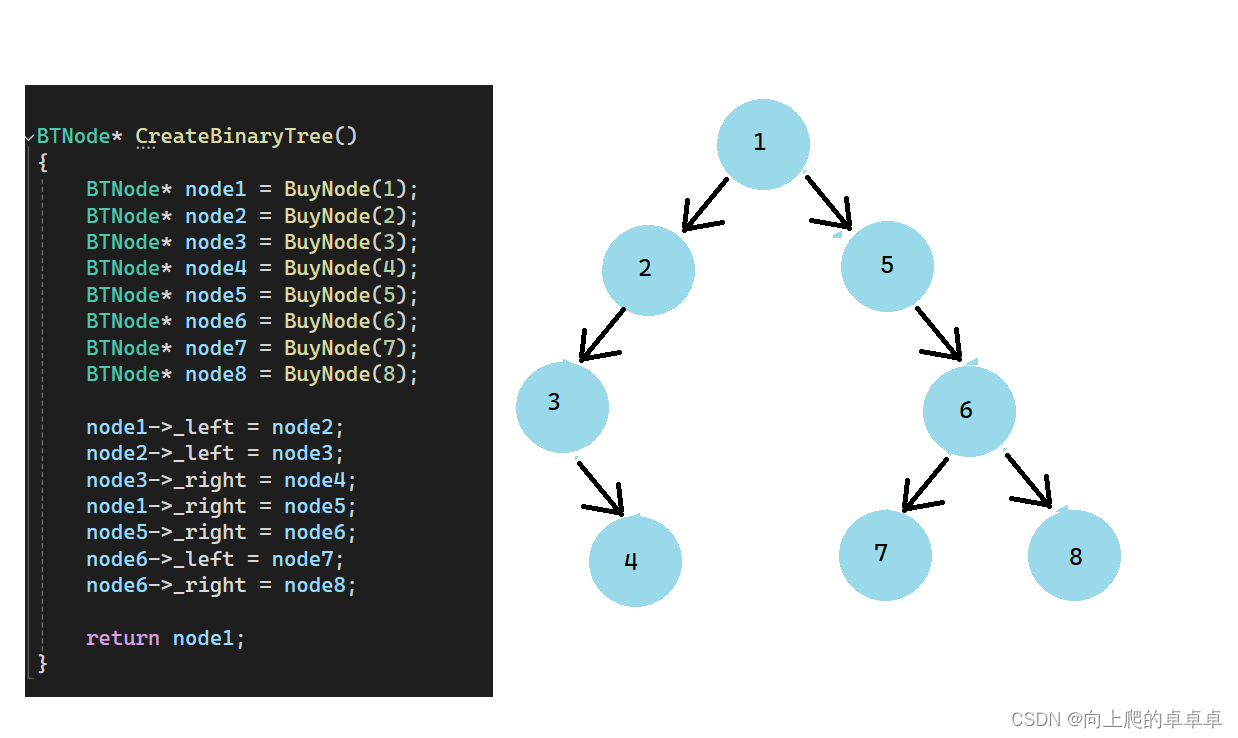
在完成二叉树的基本操作之前,我们先在这里简单的回顾一下二叉树的基本概念。
二叉树只有两个状态
- 空树
- 非空:由根结点,根节点的左子树,根结点的右子树组成

从图中可以看出,二叉树定义是递归形式的(根结点的左孩子也能看作根,其左右孩子以及对于的联系也能看成左右子树,根的右孩子同理),所以我们下面的操作都是通过递归来实现。
以下所有的操作都会使用上面手搓的树
二叉树的遍历
所谓前中后序的遍历就是根结点的先后访问顺序,所以前中后序遍历也叫前根、中根、后根遍历。
- 前序(前根)的访问顺序:根、左子树、右子树
- 中序(中根)的访问顺序:左子树、根、右子树
- 后序(后根)的访问顺序:左子树、右子树、根
这里先将遍历的原因是后续的操作,都会用到遍历的思路。

前序遍历
一般说这个树的前序遍历是[1, 2, 3, 4, 5, 6, 7, 8]
但这不是最详细的表达,最详细的表达是[1, 2, 3, NULL, 4, NULL, NULL, NULL, 5, NULL, 6, 7, NULL, NULL, 8, NULL, NULL]。
3 后面的
NULL其实是 3 的左孩子,4 后面俩个NULL代表的是 4 的左孩子和右孩子,而 5 前面的NULL代表的是 2 的右孩子,5 后面的NULL代表 5 的左孩子,7 和 8 后面的NULL都是代表他们的左右孩子。
中序
一般说这个树的中序遍历是[3, 4, 2, 1, 5, 7, 6, 8 ];
实际则是[N, 3, N, 4, N, 2, N, 1, N, 5, N, 7, N, 6, N, 8, N](N代替NULL)
由于是先访问左子树,所以第一个真正被遍历的一定是NULL。
3 前面的
N就是 3 的左孩子,4 前后的N则代表的是 4 的左右孩子,2 后面的N代表的是 2 的右孩子;5 前面的N代表 5 的左孩子,7 和 8 前后的N都代表他们的左右孩子。
后序
一般:[4, 3, 2, 7, 8, 6, 5, 1]
实际则是[N, N, N, 4, 3, N, 2, N, N, N, 7, N, N, 8, 6, 5, 1](N代替NULL)
第一个
N是 3 的左孩子,第二第三个N是 4 的左右孩子,3 后面的N是 2 的右孩子;而 2 后面的第一个N是 5 的左孩子,7 和 8 的前俩个N都是代表他们的左右孩子
注意:无论是哪种遍历,孩子之间的顺序一定是先左孩子,再是右孩子。
层序遍历
就是我们正常的思维,一层一层、从左到右的依次遍历,这种遍历方式叫广度优先遍历(BFS),而前三种遍历方式叫深度优先遍历(DFS)。
层序遍历需要依靠队列来实现。
代码实现
前中后序的遍历的大体相同,只是打印的位置不同
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}前序时printf的位置在前面printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);中序时printf的位置在中间printf("%d ", root->_data);BinaryTreePrevOrder(root->_right);后续时printf的位置在末尾printf("%d ", root->_data);
}
用图像讲解递归过程

右子树的递归过程大体相同,注意实际情况并不会开那么多的空间,而是当你使用完返回再使用的时候,是将原来的空间给重新利用了。
层序遍历的实现
在完成层序遍历之前,我们需要有队列这个数据结构(我们可以直接将以前的代码拿过来:具体代码在数据结构【队列】)
具体思路是,先创建一个队列,将二叉树的根结点存放到队列里,每遍历一个结点就删掉这个在队列里的结点,删掉的同时,将该结点的左右孩子存放到队列内部这样依次往复。
这里的类型是结点的类型,并且存放的是指针,所以要带个*号
typedef struct BinaryTreeNode* QUEUEDATA;typedef struct QNode
{QUEUEDATA _val;struct QNode* _next;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
层序遍历代码
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue* q = (Queue*)malloc(sizeof(Queue));QueueInit(q);//先把root入到队列QueuePush(q, root);//当队列尾空时,就代表以及打印完了while (!QueueEmpty(q)){//取队头数据BTNode*tmp = QueueFirst(q);//然后删除数据,我只是操作队列内部,并没有动原来的二叉树QueuePop(q);//当为空时不加数据,这就能应对根结点是空时的情况,就不需要在外面再做一次判断if (tmp == NULL){printf("N ");}//非空,将左右孩子添加到队列else{printf("%d ", tmp->_data);QueuePush(q,tmp->_left);QueuePush(q,tmp->_right);}}
}
二叉树的计算
本文计算关于树的计算有四个
- 计算树结点的个数
- 计算树的叶子结点个数
- 计算第k层的节点个数
- 计算树的高度
计算节点个数
这就很简单了,就是左右子树加自己,但每个孩子又可以分为根,左子树,右子树,当根等于空时返回0就可以了。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
这里的+1就是加自己,当你来到下面那个return时,就代表该节点并不是空节点。
计算叶子节点个数
简单的回顾一下:叶子节点就是左右孩子都为空的节点。
所以就可以判断当左右孩子都为空时,就返回 1。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
计算第k层节点个数
这个也能很好的用递归来解决,第k层是对于根节点来说的,但对于根节点的下一层来说,第k层其实是第k-1层,所以可以一直减下去,直到当k==1时,return 1。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
计算树的高度
那我就比较左子树和右子树的高度,比较出结果后再加自身的高度(比较出的高度+1)
结束递归的条件就是当我的子树为空,返回0。
// 二叉树的高度
int BinaryHeight(BTNode* root)
{if (root == NULL){return 0;}return BinaryHight(root->_left) > BinaryHight(root->_right) ? BinaryHight(root->_left) + 1: BinaryHight(root->_right) + 1;
}
这样也可以,但是如果用这个去做利扣的题是无法通过的,并不是因为程序结果错误,而是因为栈溢出。
看看为什么会栈溢出:我要比较出两个子树的长度,就一定会运行
return BinaryHight(root->_left) > BinaryHight(root->_right) ? BinaryHight(root->_left) + 1: BinaryHight(root->_right) + 1; 这有没有发现,我并没有记录比较高的值,我辛辛苦苦递归很多次才得到的左右子树中较高的子树,当我要返回高度的时候,诶?我前面的数是啥?所以我就又要进行 BinaryHight(root->_left) + 1或者BinaryHight(root->_right) + 1,这样我又会进行递归,再递归比较,然后再递归返回值->递归比较这样一直下去,直到最低层(root == NULL)。
所以,我们需要变量来记录两颗子树的高度,这样我们再比较的时候就不会重复递归了。
// 二叉树的高度
int BinaryHeight(BTNode* root)
{if (root == NULL){return 0;}//记录左树的高度int L = BinaryHight(root->_left);//记录右树的高度int R = BinaryHight(root->_right);//比较出较高的,加上自己这一层的高度return (L > R ? L : R) + 1;
}
二叉树的创建和销毁
二叉树的创建(前序)
这题是使用前序来创建二叉树
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
'#'号代表空,a是数组,n是长度,pi是下标
先创建父亲节点,然后左子树 -> 创建左子树当中的父亲节点,然后创建左子树 —>直到这时的数据是'#'返回NULL,创建右子树,右子树创建完,函数自然结束,回到上一层让上一层来创建右子树。
当pi等于n的时候,就代表已经遍历完该数组了,这条数组里的数据已经被我创建成一个二叉树了;这时候就返回NULL;这个判断放在函数的开头。
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
//当下标与长度相等,返回NULLif (*pi == n){return NULL;}if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));//先创建根节点,再创建左子树,再创建右子树root->_data = a[(*pi)++];root->_left = BinaryTreeCreate(a, n, pi);//先创建左子树root->_right = BinaryTreeCreate(a, n, pi);//再创建右子树return root;//返回根节点
}
二叉树的销毁(后序)
这题我们采用后序来删除,是因为后续并不需要记录节点,是从底层一点一点销毁节点,当我左右子树的节点都销毁了(或者都为NULL),才销毁我的根节点。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
既然是销毁,那么就会修改原来的值,所以我们就传二叉树根节点的地址。
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (root == NULL || *root == NULL){return;}BinaryTreeDestory(&(*root)->_left);//先销毁左子树BinaryTreeDestory(&(*root)->_right);//再销毁右子树//当左右节点都被销毁或者都为NULLfree(*root);//最后再销毁根节点
}
结语
到这里二叉树的基本函数就讲完啦。
最后感谢您能阅读完此片文章,如果有任何建议或纠正欢迎在评论区留言,也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获,点一个小小的赞就是我创作的巨大动力,谢谢!!!