本篇文章是博主在人工智能等领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对人工智能等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在AI学习笔记：

      AI学习笔记（7）---《聚类算法（1）---最大最小距离、C-均值算法》

聚类算法（1）---最大最小距离、C-均值算法

目录

一、聚类算法背景知识

二、常用聚类算法介绍

2.1 最大最小距离聚类算法

2.2 C-均值算法

三、聚类算法的Python实现 

四、聚类算法Python实现结果

五、小结

---

一、聚类算法背景知识

        聚类是一种无监督学习方法，旨在将数据集中的对象按照某种相似性标准划分成若干组别。聚类算法在数据挖掘、模式识别、图像处理等领域有着广泛的应用。其目标是发现数据内在的结构和规律，以便对数据进行理解和分析。聚类算法的背景可以追溯到数十年前，在统计学、机器学习和模式识别领域得到了长足的发展。

其他聚类算法见：

聚类算法（2）--- ISODATA算法

1.1 聚类算法的历史

        聚类算法的研究始于20世纪60年代，最初主要关注于数学统计方面的方法。随着数据挖掘和机器学习技术的兴起，聚类算法逐渐成为研究热点。传统的聚类方法包括K均值聚类、层次聚类、DBSCAN（基于密度的聚类）、高斯混合模型等。这些方法在处理不同类型的数据和问题时展现出各自的优势和局限性。

1.2 聚类算法的应用

        聚类算法在各个领域都有着广泛的应用。在商业领域，聚类算法被用于市场细分、客户分类、产品推荐等方面，帮助企业更好地了解消费者需求。在生物信息学领域，聚类算法被用于基因表达数据分析，帮助科学家识别潜在的生物学模式和相关基因。在图像处理领域，聚类算法被用于图像分割、目标识别和特征提取，为计算机视觉和模式识别领域提供重要支持。

1.3 聚类算法的挑战与发展

        尽管聚类算法已经取得了许多成功应用，但仍然存在一些挑战和问题。例如，对于大规模高维数据的处理、噪声和异常值的影响、簇形状的多样性等问题需要进一步研究。近年来，随着深度学习和神经网络技术的发展，新的聚类算法也在不断涌现。诸如谱聚类、t-SNE等新型聚类方法正在逐渐受到人们的关注，并在一些领域展示出更好的性能。

---

二、常用聚类算法介绍

2.1 最大最小距离聚类算法

        最大最小距离聚类算法是一种基于距离度量的聚类方法，旨在根据每个样本点与其他点的最大最小距离之比来确定簇的核心点。该算法的提出源于对距离度量在聚类分析中的重要性的认识，同时也受到K-均值算法等传统聚类方法的启发

2.1.1算法原理

        最大最小距离聚类算法的核心思想是通过计算每个样本点与其他点的距离，找到其最大最小距离之比，从而判断其是否为簇的核心点。具体步骤包括选择合适的θ值作为阈值，对每个样本点计算与其他点的最大距离和最小距离，然后进行比值计算。若该比值大于θ，则将该点归为某个簇的核心点。

2.1.2实验应用

        在实际应用中，最大最小距离聚类算法可以用于图像分割、异常检测、模式识别等领域。例如在图像分割中，可以利用该算法对图像进行自动分割，将相邻的像素点按照它们的灰度级别划分为不同的区域，实现目标定位和识别。

2.2 C-均值算法

        C-均值算法（K-means）是一种常见的聚类分析方法，被广泛应用于数据挖掘和模式识别领域。其基本思想是通过迭代更新簇中心点的位置，将数据划分为K个簇，使得簇内的数据点尽可能接近各自的中心点。

2.2.1算法原理

        C-均值算法的核心思想是不断迭代地更新每个簇的中心点，直至满足收敛条件。具体过程包括初始化K个簇的中心点，计算每个样本点与各个中心点的距离，并将其归入距离最近的簇中，然后更新每个簇的中心点位置，再次重新分配样本点，如此往复直至收敛。

2.2.2实验应用

        均值算法广泛应用于数据挖掘和图像处理领域。它可用于市场细分、客户分类、异常检测等商业应用，也可以用于图像分割、特征提取等图像处理任务。例如，在医学影像处理中，C-均值算法可用于对医学图像中的组织结构进行分割，以辅助医生诊断疾病。

---

三、聚类算法的Python实现 

        给定样本集 X = {(0, 0)', (0, 1)', (4, 4)', (4, 5)', (5, 4)', (5, 5)', (1, 0)'}

3.1 最大最小距离聚类算法python实现

最大最小距离聚类算法是一种基于距离度量的聚类方法，其算法流程可以简要概括如下。

3.1.1算法流程

（1）初始化参数：首先选择合适的簇数K和阈值θ，并随机初始化K个点作为各个簇的中心。

（2）计算距离：对于数据集中的每个样本点，计算它与其他所有点的距离。这里通常使用欧氏距离或曼哈顿距离等距离度量方式。

（3）计算最大最小距离比值：对于每个样本点，计算它与其他所有点的最大距离和最小距离，并计算它们的比值。这一步旨在判断每个样本点是否为簇的核心点。

（4）确认核心点：根据计算得到的最大最小距离比值和阈值θ进行判断，将满足条件的样本点确定为簇的核心点。

（5）分配样本点：将未被确定为核心点的样本点分配给距离最近的核心点所在的簇。

（6）更新簇的中心：对每个簇内的样本点重新计算中心点位置，以此为基础重新进行核心点的判断和样本点的分配，直至满足终止条件（如收敛）。

（7）输出结果：最终得到K个簇，每个簇包含若干个样本点，完成聚类过程。

3.1.2算法python程序

导入需要的python库

import math
import random
import numpy as np  # 导入NumPy库，用于处理数组
import matplotlib.pyplot as plt  # 导入matplotlib.pyplot库，用于绘图
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 使用微软雅黑字体
plt.rcParams['axes.unicode_minus'] = False  # 处理负号显示异常

开始聚类函数

def start_cluster(data, t):# 聚类中心集，任意选取样本作为第一个聚类中心Z1zs = [data[random.randint(0, 6)]]# 寻找第二个聚类中心Z2,并计算阈值thresholdthreshold = step2(data, t, zs)# 寻找所有的聚类中心get_clusters(data, zs, threshold)# 按最近邻分类（最小距离准则）results = classify(data, zs, threshold)return results, zs

分类函数

def classify(data, zs, threshold):results = [[] for _ in range(len(zs))]for aData in data:min_distance = thresholdindex = 0for i in range(len(zs)):temp_distance = get_distance(aData, zs[i])if temp_distance < min_distance:min_distance = temp_distanceindex = iresults[index].append(aData)return results

寻找所有的聚类中心

def get_clusters(data, zs, threshold):max_min_distance = 0index = 0for i in range(len(data)):min_distance = []for j in range(len(zs)):distance = get_distance(data[i], zs[j])min_distance.append(distance)min_dis = min(dis for dis in min_distance)if min_dis > max_min_distance:max_min_distance = min_disindex = iif max_min_distance > threshold:zs.append(data[index])# 迭代get_clusters(data, zs, threshold)  # 继续寻找聚类中心

寻找Z2,并计算阈值T

def step2(data, t, zs):distance = 0index = 0for i in range(len(data)):temp_distance = get_distance(data[i], zs[0])if temp_distance > distance:distance = temp_distanceindex = i# 将Z2加入到聚类中心集中zs.append(data[index])# 计算阈值Tthreshold = t * distancereturn threshold

计算两个模式样本之间的欧式距离

def get_distance(data1, data2):distance = 0for i in range(len(data1)):distance += pow((data1[i] - data2[i]), 2)return math.sqrt(distance)

程序主函数

if __name__ == '__main__':data = [[0, 0], [0, 1], [4, 4], [4, 5], [5, 4], [5, 5], [1, 0]]t = 0.8  # 比例因子colors = ['r', 'g', 'b', 'c', 'm', 'y']  # 颜色列表result, centroids = start_cluster(data, t)for i in range(len(result)):print("----------第" + str(i + 1) + "个聚类----------")print(result[i])plt.scatter(np.array(result[i])[:, 0], np.array(result[i])[:, 1], c=colors[i], label=f'Cluster {i + 1}', marker="o")plt.scatter(np.array(centroids)[:, 0], np.array(centroids)[:, 1], c='k', marker='x', label='Centroids')plt.title('MaxMin Clustering')plt.xlabel('X')plt.ylabel('Y')plt.legend()plt.show()

3.1.3算法注意事项

        最大最小距离聚类算法相对较为简单，但在实际应用中需要谨慎选择合适的参数和距离度量方式，以获得较好的聚类效果。

3.2 模糊C-均值聚类算法python实现

考虑到近期研究方向关注于概率的相关知识，为结合目前的研究进展，在了解到模糊C-均值聚类算法的基本知识后，选择采用模糊C-均值聚类算法完成本次实验。

模糊C-均值聚类算法是一种常见的基于的聚类方法，其算法流程如下：

3.2.1算法流程

（1）初始化：设置聚类数目k和模糊度参数m，以及终止条件（如最大迭代次 数或收敛阈值）。初始化聚类中心向量和隶属度矩阵。

（2）计算隶属度矩阵：对每个数据点，计算其与各个聚类中心的欧氏距离，并 根据公式计算隶属度。

（3）更新聚类中心：根据隶属度矩阵，更新每个聚类中心

（4）判断是否满足终止条件：若未达到设定的终止条件，则返回步骤2继续迭 代；否则，结束迭代。

（5）输出结果：输出最终的聚类中心和隶属度矩阵，将数据点按照隶属度分配 到对应的聚类中心。

3.2.2算法python程序

导入需要的python库

import numpy as np  # 导入NumPy库，用于处理数组
import random  # 导入random库
import matplotlib.pyplot as plt  # 导入matplotlib.pyplot库，用于绘图

相关函数定义

def euclidean_distance(a, b):return np.linalg.norm(a - b)  # 计算欧氏距离# 初始化
def initialize_membership_matrix(num_samples, num_clusters):membership_matrix = np.random.rand(num_samples, num_clusters)  # 随机初始化隶属度矩阵membership_matrix = membership_matrix / np.sum(membership_matrix, axis=1)[:, None]  # 归一化隶属度矩阵return membership_matrixdef update_centroids(data, membership_matrix, num_clusters):# 更新聚类中心centroids = np.dot(data.T, membership_matrix ** 2) / np.sum(membership_matrix ** 2, axis=0)  return centroids.Tdef update_membership_matrix(data, centroids, fuzziness):# 计算数据点到各聚类中心的距离distances = np.array([[euclidean_distance(point, centroid) for centroid in centroids] for point in data])membership_matrix = 1 / distances ** (2 / (fuzziness - 1))  # 更新隶属度矩阵membership_matrix = membership_matrix / np.sum(membership_matrix, axis=1)[:, None]  # 归一化隶属度矩阵return membership_matrixdef cmeans_clustering(data, num_clusters, fuzziness, max_iterations, epsilon):membership_matrix = initialize_membership_matrix(len(data), num_clusters)  # 初始化隶属度矩阵centroids = update_centroids(data, membership_matrix, num_clusters)  # 更新聚类中心for _ in range(max_iterations):old_centroids = centroidsmembership_matrix = update_membership_matrix(data, centroids, fuzziness)  # 更新隶属度矩阵centroids = update_centroids(data, membership_matrix, num_clusters)  # 更新聚类中心if np.linalg.norm(centroids - old_centroids) < epsilon:  # 判断是否满足停止条件breakreturn centroids, membership_matrix

主函数

if __name__ == '__main__':# 数据data = np.array([[0, 0], [0, 1], [4, 4], [4, 5], [5, 4], [5, 5], [1, 0]])# 调用 C-means 算法进行聚类num_clusters = 2  # 指定簇的数量fuzziness = 2  # 设置模糊因子max_iterations = 10  # 最大迭代次数epsilon = 0.01  # 容差centroids, membership_matrix = cmeans_clustering(data, num_clusters, fuzziness, max_iterations, epsilon)# 可视化聚类结果cluster_labels = np.argmax(membership_matrix, axis=1)  # 获取样本所属的簇colors = ['r', 'g', 'b', 'c', 'm', 'y']  # 颜色列表for i in range(num_clusters):cluster_points = data[cluster_labels == i]# 根据簇标签绘制散点图plt.scatter(cluster_points[:, 0], cluster_points[:, 1], c=colors[i], label=f'Cluster {i+1}')  plt.scatter(centroids[:, 0], centroids[:, 1], c='k', marker='x', label='Centroids')  # 绘制聚类中心plt.title('C-means Clustering')  # 设置图表标题plt.xlabel('X')  # 设置X轴标签plt.ylabel('Y')  # 设置Y轴标签plt.legend()  # 显示图例plt.show()  # 展示图表

3.2.3算法注意事项

        在实际应用中，为了提高算法的效率和稳定性，通常会采用多次随机初始化和选择最优的聚类结果、选择合适的距离度量方式、以及设定合理的终止条件等策略。

---

四、聚类算法Python实现结果

4.1最大最小距离算法实验结果

相关参数设置：

        对最大最小算法的结果影响较大的参数是阈值，下面分析该参数对于聚类效果的影响：

        1.当阈值=0.5时：

        如图所示，当阈值=0.5时，算法可以很好地将样本集分类为红蓝两类，并且加粗的圆点为类簇的聚类中心。通过实验结果可以看出：当阈值选取正确的时候，可以正确地将样本集聚类成功。        

        2.当阈值=0.2时：

        如图所示，当阈值=0.2时，该算法将样本集错误地分成了四类。这是因为阈值太小的时候，某些不是新类簇的点也满足了算法的阈值条件，导致了新类簇的产生，因而聚类错误。

        3.当阈值=1时：

        如图所示，当阈值=1时，该算法将样本集错误地分成了一类。=1其实并不满足算法的前提条件，但是为了演示算法的分类原理故在此设置此类情况。如图所示，当=1时，样本集只剩下一个类别。这是因为当阈值太大的时候，某些原本是不同类簇的点由于无法满足阈值条件，导致被分到了同一类簇中去。

        综上所述，最大最小算法的聚类结果的正确性与阈值的选取密切相关，只有阈值选取合理的时候才能正确分类，若阈值太小可能会导致聚类数增多，若阈值太大则可能导致聚类数变少。

4.2 C-means算法实验结果

        相关参数设置：簇的数量 = 2，模糊因子 = 2，最大迭代次数 = 100，容差 = 0.01。

        数据可视化聚类输出结果：

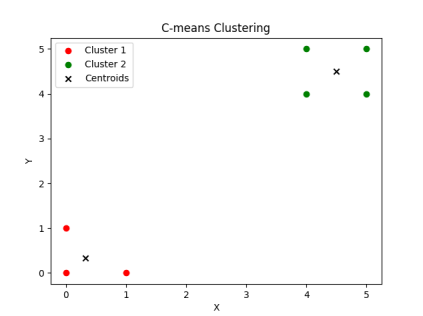
        最终运行结果的隶属度矩阵：

        由隶属度矩阵可知，取每个样本点概率最大的值，将其分类到相应的类，即可得到最终的分类结果。

修改簇的数量 = 3；

修改簇的数量 = 4；

        由上图可知，修改不同聚类的数量，可以得到相应的聚类的数量。

---

五、小结

        最大最小距离聚类算法、C-均值聚类算法和ISODATA算法都是常用的聚类算法。它们在实际应用中都能够成功地对提供的数据进行聚类，从而发现数据中的潜在模式和结构。这些算法在实现数据聚类时，需要根据具体的数据特点和应用需求进行选择和调优。

        最大最小距离聚类算法着重于样本点之间的距离比值，能够有效地识别出分离明显的簇。其简单直观的实现方式使其在一些特定场景下表现良好，尤其对于具有离群点的数据集有一定的鲁棒性。然而，对于簇形状复杂、密度不均匀的数据集，该算法可能表现不佳。

        C-均值聚类算法适用于各个簇的形状近似球形、簇内数据点密集且分布均匀的数据集。由于算法简单高效，在大数据集上也能够较好地工作。然而，C-均值算法对初始簇中心的选择敏感，可能收敛于局部最优解，因此需要仔细调整参数以获得较好的聚类结果。

---

     文章若有不当和不正确之处，还望理解与指出。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请联系博主删除。如有错误、疑问和侵权，欢迎评论留言联系作者，或者私信联系作者。