目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2023年,J Bai受到双曲正弦余弦函数启发,提出了双曲正弦余弦优化算法(Sinh Cosh optimizer, SCHO)。


2.算法原理
2.1算法思想
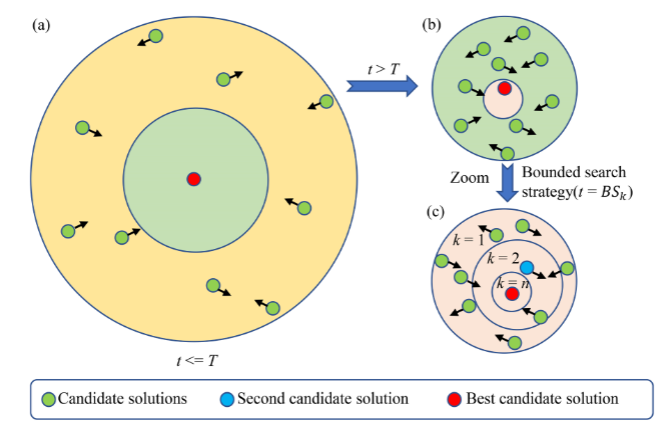
SCHO灵感来源于Sinh函数和Cosh函数特性,其包括四个步骤:探索和开发阶段、有界搜索策略和切换机制。
2.2算法过程
探索阶段
探索阶段和开发阶段平衡基于:
T = f l o o r ( M a x _ i t e r a t i o n c t ) (1) T=floor\left(\frac{Max\_iteration}{ct}\right)\tag{1} T=floor(ctMax_iteration)(1)
探索位置更新:
X ( i , j ) t + 1 = { X b e s t ( j ) + r 1 × W 1 × X ( i , j ) i , r 2 > 0.5 X b e s t ( j ) − r 1 × W 1 × X ( i , j ) i , r 2 < 0.5 (2) \left.X_{(i,j)}^{t+1}=\left\{\begin{array}{ll}X_{best}^{(j)}+r_1\times W_1\times X_{(i,j)}^i, r_2>0.5\\X_{best}^{(j)}-r_1\times W_1\times X_{(i,j)}^i, r_2<0.5\end{array}\right.\right.\tag{2} X(i,j)t+1={Xbest(j)+r1×W1×X(i,j)i,r2>0.5Xbest(j)−r1×W1×X(i,j)i,r2<0.5(2)
W1为第一探索阶段Xt (i,j)的权重系数,控制第一阶段候选解远离自身,逐步向最优解探索:
W 1 = r 3 × a 1 × ( cosh r 4 + u × sinh r 4 − 1 ) (3) W_1=r_3\times a_1\times(\cosh r_4+u\times\sinh r_4-1)\tag{3} W1=r3×a1×(coshr4+u×sinhr4−1)(3)
U是控制探索精度的敏感系数,参数a1:
a 1 = 3 × ( − 1.3 × t Max_iteration + m ) (4) a_1=3 \times\left(-1.3\times\frac{t}{\text{Max\_iteration}}+ m\right)\tag{4} a1=3×(−1.3×Max_iterationt+m)(4)
在第二阶段的探索中,搜索个体几乎不受最优解的影响,因此它们在当前位置的基础上非定向地探索下一个位置:
X ( i j ) t + 1 = { X ( i , j ) t + ∣ ε × W 2 × X b e s t ( j ) − X ( i , j ) t ∣ , r 5 > 0.5 X ( i , j ) t − ∣ ε × W 2 × X b e s t ( j ) − X ( i , j ) t ∣ r 5 < 0.5 (5) \left.X_{(ij)}^{t+1}=\left\{\begin{array}{ll}X_{(i,j)}^t+\Big|\varepsilon\times W_2\times X_{best}^{(j)}-X_{(i,j)}^t\Big|, r_5>0.5\\X_{(i,j)}^t-\Big|\varepsilon\times W_2\times X_{best}^{(j)}-X_{(i,j)}^t\Big| r_5<0.5\end{array}\right.\right.\tag{5} X(ij)t+1=⎩ ⎨ ⎧X(i,j)t+ ε×W2×Xbest(j)−X(i,j)t ,r5>0.5X(i,j)t− ε×W2×Xbest(j)−X(i,j)t r5<0.5(5)
W2是第二阶段探索中X(j)最优的权重系数:
W 2 = r 6 × a 2 (6) W_2=r_6\times a_2\tag{6} W2=r6×a2(6)
a2是单调递减函数:
a 2 = 2 × ( − t M a x _ i t e r a t i o n + n ) (7) a_2=2 \times\left( -\frac{t}{Max\_iteration}+n\right)\tag{7} a2=2×(−Max_iterationt+n)(7)
开发阶段
为了充分利用搜索空间,将开发分为两个阶段,并在整个迭代中进行。在第一个开发阶段,对X的附近空间进行开发:
X ( i , j ) t + 1 = { X b e s t ( j ) + r 7 × W 3 × X ( i , j ) t , r 8 > 0.5 X b e s t ( j ) − r 7 × W 3 × X ( i , j ) t , r 8 < 0.5 (8) X_{(i,j)}^{t+1}=\begin{cases} X_{best}^{(j)}+r_{7}\times W_{3}\times X_{(i,j)}^{t}, r_{8}>0.5\\ X_{best}^{(j)}-r_{7}\times W_{3}\times X_{(i,j)}^{t}, r_{8}<0.5\end{cases}\tag{8} X(i,j)t+1={Xbest(j)+r7×W3×X(i,j)t,r8>0.5Xbest(j)−r7×W3×X(i,j)t,r8<0.5(8)
W3是第一阶段开发的权重系数,控制候选解从近到远地开发自身周围的搜索空间:
W 3 = r 9 × a 1 × ( cosh r 10 + u × sinh r 10 ) (9) W_3=r_9\times a_1\times(\cosh r_{10}+u\times\sinh r_{10})\tag{9} W3=r9×a1×(coshr10+u×sinhr10)(9)
在开发的第二阶段,将执行候选解决方案围绕所获得的最优解进行深度开发,并且围绕最优解的开发强度将随着迭代的增加而增加:
X ( i , j ) t + 1 = X ( i , j ) t + r 11 × sinh r 12 c o s h r 12 ∣ W 2 × X b e s t ( j ) − X ( i , j ) t ∣ (10) X_{(i,j)}^{t+1}=X_{(i,j)}^{t}+r_{11}\times\frac{\sinh r_{12}}{coshr_{12}}\left|W_{2}\times X_{best}^{(j)}-X_{(i,j)}^{t}\right|\tag{10} X(i,j)t+1=X(i,j)t+r11×coshr12sinhr12 W2×Xbest(j)−X(i,j)t (10)
W2控制第二开采阶段的程度。其绝对值在以后的迭代中逐渐增大,开发程度也随之增大。
有界搜索策略
为了充分利用潜在的搜索空间,SCHO在后期采用了一种类似于动物狩猎的策略,称为有界搜索策略。该策略的每一个起始点由下式计算:
B S k + 1 = B S k + f l o o r ( M a x _ i t e r a t i o n − B S k α ) (11) BS_{k+1}=BS_k+floor\Bigg(\frac{Max\_iteration-BS_k}{\alpha}\Bigg)\tag{11} BSk+1=BSk+floor(αMax_iteration−BSk)(11)
α为控制潜力空间深部勘探开发精度的敏感系数,BS1表述为:
B S 1 = f l o o r ( M a x _ i t e r a t i o n β ) (12) BS_1=floor\left(\frac{Max\_iteration}{\beta}\right)\tag{12} BS1=floor(βMax_iteration)(12)
其中β控制启动有界搜索策略的值,并设置为1.55。当SCHO每次都使用有界搜索策略时,上下界设置为:
u b k = X b e s t ( j ) + ( 1 − t M a x − i t e r a t i o n ) × ∣ X b e s t ( j ) − X s e c o n d ( j ) ∣ l b k = X b e s t ( j ) − ( 1 − t M a x _ i t e r a t i o n ) × ∣ X b e s t ( j ) − X s e c o n d ( j ) ∣ (13) ub_k=X_{best}^{(j)}+\left(1-\frac{t}{Max_-iteration}\right)\times\left|X_{best}^{(j)}-X_{second}^{(j)}\right|\\ lb_k=X_{best}^{(j)}-\left(1-\frac{t}{Max\_iteration}\right)\times\left|X_{best}^{(j)}-X_{second}^{(j)}\right|\tag{13} ubk=Xbest(j)+(1−Max−iterationt)× Xbest(j)−Xsecond(j) lbk=Xbest(j)−(1−Max_iterationt)× Xbest(j)−Xsecond(j) (13)
切换机制
在SCHO中,提出了一种带有Sinh和Cosh的转换机制,实现了勘探和开发之间的转换:
A = ( p − q × ( t M a x − i t e r a t i o n ) ( cosh t M a x − i t r a t i o n sinh t M a x − i t e r a t i o n ) ) × r 13 (14) A=\left(p-q\times\left(\frac{t}{Max_-iteration}\right)^{\left(\frac{\cosh\frac{t}{Max-itration}}{\sinh\frac{t}{Max-iteration}}\right)}\right)\times r_{13}\tag{14} A= p−q×(Max−iterationt)(sinhMax−iterationtcoshMax−itrationt) ×r13(14)
流程图
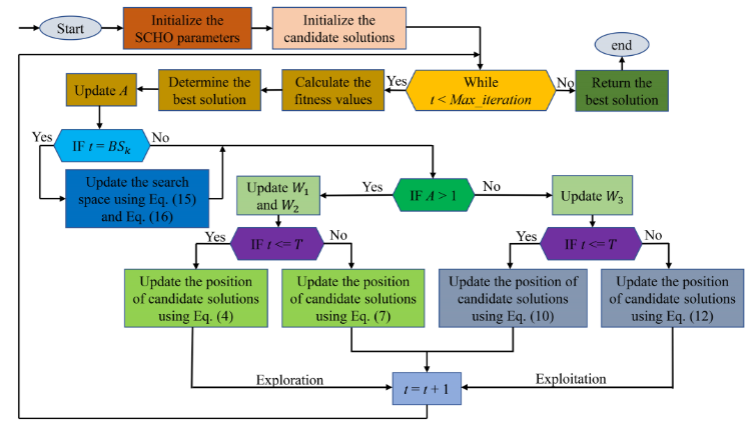
伪代码

3.结果展示
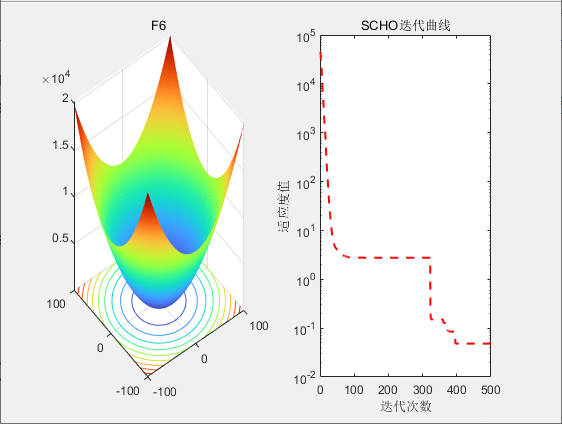
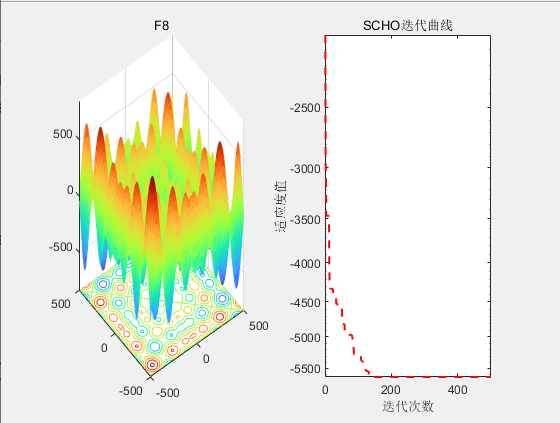
4.参考文献
[1] Bai J, Li Y, Zheng M, et al. A sinh cosh optimizer[J]. Knowledge-Based Systems, 2023, 282: 111081.