空间复杂度线性表，顺序表尾插。

各位少年，大家好，我是那一脸阳光，本次分享的主题是时间复杂度和空间复杂度还有顺序表文章讲解和分享，如有不对可以评论区指导。
在这里插入图片描述

时间复杂度例题

 // 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N){if(N < 3)return 1;return Fib(N-1) + Fib(N-2);}

这块的时间复杂度为O（2^N)次方可以看到这个代码是个等比数列，我们通过下面的图举个例子。
0
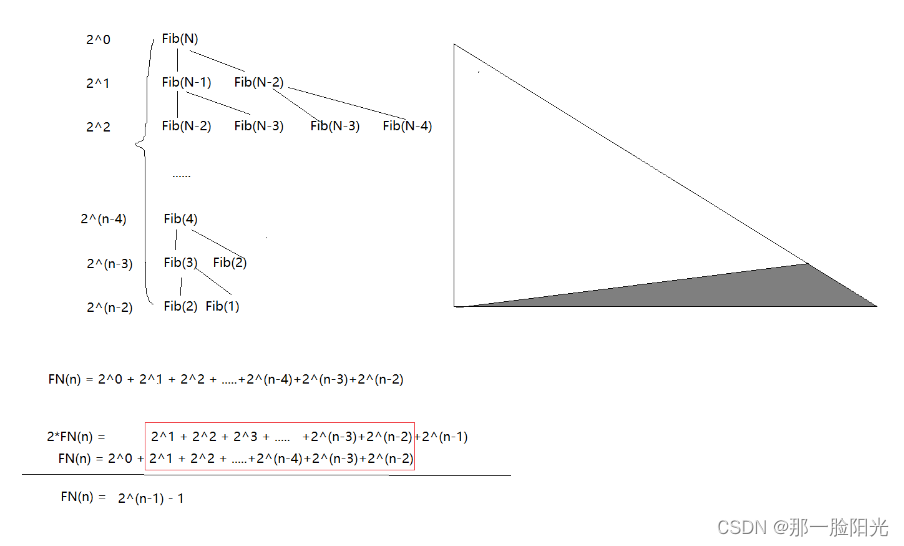
在这里插入图片描述
我们发现每次FIb（N）开始每次递归都变成两个，然后通过错位即可算出 FN的公式是2^(n-1)-1,这个减一是减刚开始项。
OJ题消失的数字
https://leetcode-cn.com/problems/missing-number-lcci/
数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？

{int x = 0;for (int i = 0; i < numsSize; i++){x ^= nums[i];}for (int i = 0; i < numsSize+1; i++){x ^= i;}return x;
}

这段代码是一段单身狗问题，1^1是0 ，2^{2也是0大家注意第二个循环即可，这种题一般非常的简单的，0}a都是0 如果对这里不太懂可以复习一下单身狗问题。

空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因
此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
在这里插入图片描述

冒泡排序的空间复杂度


```c// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n){assert(a);for (size_t end = n; end > 0; --end{}}int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;

冒泡排序的时间复杂度在O（N^2),空间复杂度是O（1），因为这个没有额外消耗，或者有代码创造变量。

 // 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n){if(n==0)return NULL;}long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray

这段代码时间复杂度是O（N），空间复杂度也是O（N），因为这里的动态内存分配开辟了n+1个空间。

递归的空间复杂度

例子一
// 计算阶乘递归Fac的空间复杂度？

long long Fac(size_t N){if(N == 0)return 1;return Fac(N-1)*N;}

这里的每次递归都在栈中创建空间，每次递归都会创建一定的空间，所以空间复杂度是O（N）。

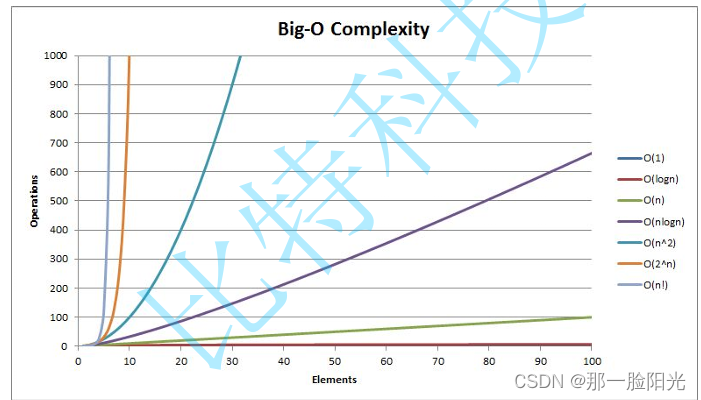
常见复杂度对比
一般算法常见的复杂度如下：
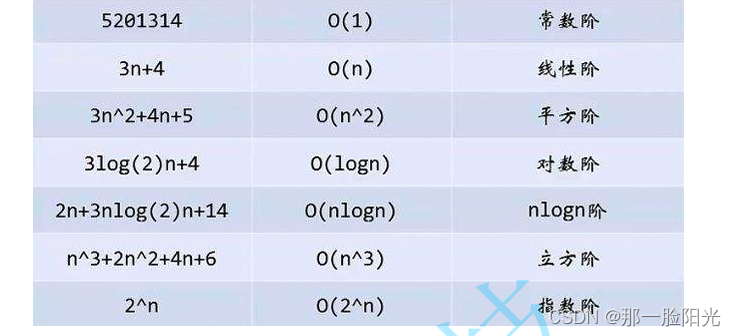
在这里插入图片描述

OJ题逆置
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
在这里插入图片描述
这里比如说N是7 K是3 前三段逆置，后四个再逆置，最后整体逆置，但是这种方法一般人能不出来，所以还有其他方法，这段代码时间复杂度是O（N^2)，空间复杂度是O（1），这里接受另外一种写法比较常用的空间换时间。

在这里插入图片描述
这里我们开创一个a的时间再开创一个tmp数组，然后再把tmp数组拷贝到a数组里头，然后销毁tmp数组即可，这样以空间换时间的方法。

这道题中三段逆置最优，其次就是空间换时间，这种方法是最优的，但空间复杂度会上涨到O（N）

 void reverse(int*a,int left,int right){while(left<right){int tmp=a[left];a[left]=a[right];a[right]=tmp;++left--right;}}void rotate(int*nums,int numsSize,int k)if（k>numsSize)k%=numsSize;reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums,0,numsSize-1);}

这段代码，完成了 三段三次逆置，接下来介绍空间换时间的逆置方法。
void rotate(int*nums,int numsSize,int k)
{
if(k>numsSize)
k%=numsSize； 
int*tmp=(int*)malloc(sizeof(int)*numsSize);
memcpy(tmp+k,nums,sizeof(int)*(numsSize-k);
memcpy(tmp,nums+numsSize-k,sizeof(int）*（k)）；
memcpy(nums,tmp.sizeof(int)*(numsSize));
free(tmp);
tmp=NULL;
}

线性表

线性表（linear list）
是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结
构，常见的线性表：顺序表、链表、栈、队列、字符串…
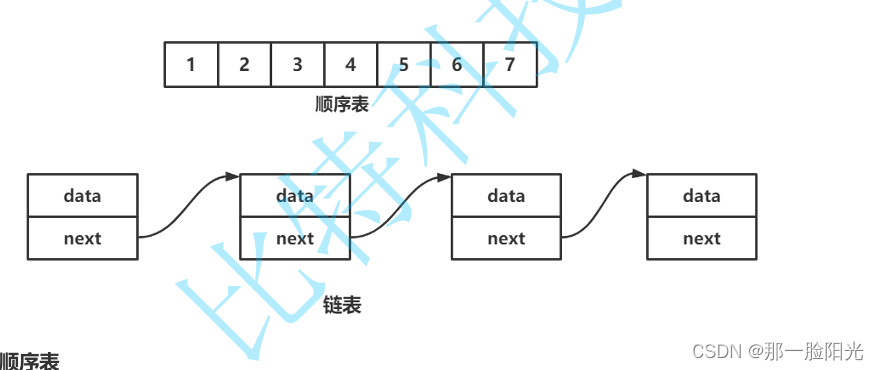
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。
在这里插入图片描述

u 在这里插入图片描述
顺序表本质是数组，如果我们想在顺序表删除第一个人我们删除的方法就是覆盖。

每个数据都往前进去一步，这样就可以实现删除覆盖了。

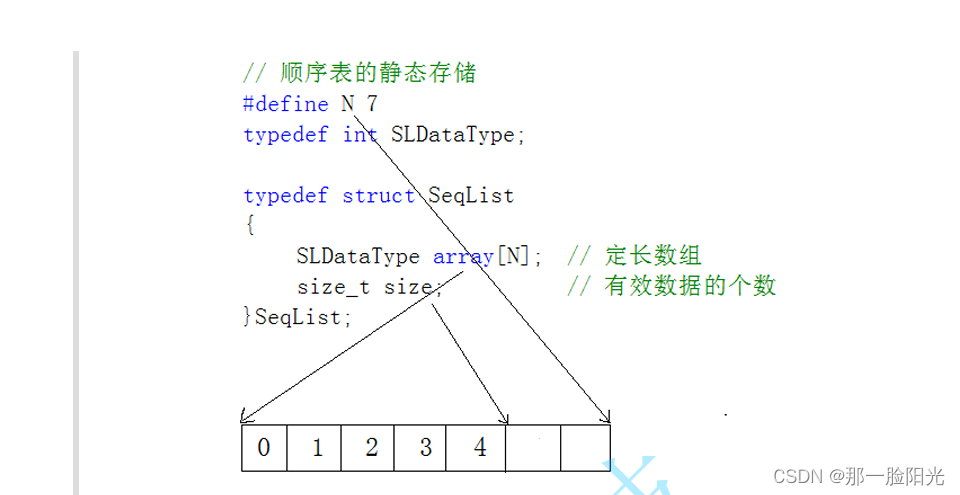
上面是静态顺序表数组长度和有效数据个数。
静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空间开多了浪
费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实现动态顺序表我们实现一下尾插

#include"SeqList.h"
void SLInit(SL* psl)
{psl->a = (SLDatatype*)malloc(sizeof(SLDatatype)*4);if (psl->a == NULL){perror("malloc fail");return;}psl->capacity = 4;psl->size = 0;
}void SLDestroy(SL* psl)
{free(psl->a);psl->a = NULL;psl->size = 0;psl->capacity = 0;
}void SLPrint(SL* psl)
{for (int i = 0; i < psl->size; i++){printf("%d ", psl->a[i]);}printf("\n");
}void SLCheckCapacity(SL* psl)
{if (psl->size == psl->capacity){SLDatatype* tmp = (SLDatatype*)realloc(psl->a, sizeof(SLDatatype) * psl->capacity * 2);if (tmp == NULL){perror("realloc fail");return;}psl->a = tmp;psl->capacity *= 2;}
}void SLPushBack(SL* psl, SLDatatype x)
{//psl->a[psl->size] = x;//psl->size++;SLCheckCapacity(psl);psl->a[psl->size++] = x;
}void SLPushFront(SL* psl, SLDatatype x);
void SLPopBack(SL* psl);
void SLPopFront(SL* psl);

这里主要实现三个部分创建空间释放空间，然后通过数组进行尾部插入，这里只实现了最简单的尾插。剩下部分我给大家写出来大家可以去编译器敲一敲。2

#pragma once
#include<stdio.h>
#include<stdlib.h>// 静态的顺序表
// 给小了不够用，给多了浪费
//#define N 10000
//typedef int SLDatatype;
//struct SeqList
//{
//	SLDatatype a[N];
//	int size;
//};// 动态顺序表
//typedef double SLDatatype;
typedef int SLDatatype;
typedef struct SeqList
{SLDatatype* a;int size;       // 存储的有效数据的个数int capacity;   // 容量
}SL;void SLInit(SL* psl);
void SLDestroy(SL* psl);void SLPrint(SL* psl);//STL命名风格
void SLPushBack(SL* psl, SLDatatype x);
void SLPushFront(SL* psl, SLDatatype x);
void SLPopBack(SL* psl);
void SLPopFront(SL* psl);

#include "SeqList.h"int main()
{SL s;SLInit(&s);SLPushBack(&s, 1);SLPushBack(&s, 2);SLPushBack(&s, 3);SLPushBack(&s, 4);SLPushBack(&s, 5);SLPushBack(&s, 6);SLPushBack(&s, 6);SLPushBack(&s, 6);SLPushBack(&s, 6);SLPrint(&s);SLDestroy(&s);return 0;
}