快去复习吧+++常用算法及参考算法递推法++穷举法++排序（冒泡、选择）++查找（顺序、折半）++字符串处理++方程求根++无穷级数求和

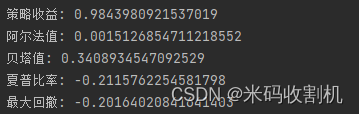
接上：常用算法及参考算法（1）累加（2）累乘（3）素数（4）最大公约数（5）最值问题（6）迭代法

在这里插入图片描述

常用算法及参考算法

7. 递推法

递推法通常用于通过已知的前一项或几项来计算数列的下一项。例如，斐波那契数列：

#include <stdio.h>int fibonacci(int n) {if (n <= 1) return n;return fibonacci(n - 1) + fibonacci(n - 2);
}int main() {int n = 10;printf("The %dth Fibonacci number is %d\n", n, fibonacci(n));return 0;
}

（注意：上述斐波那契实现是递归的，但对于大数可能效率较低。通常使用迭代递推实现。）

8. 穷举法

穷举法用于遍历所有可能的解。例如，找出1到100之间的所有素数：

#include <stdio.h>
#include <stdbool.h>bool is_prime(int num) {if (num <= 1) return false;for (int i = 2; i * i <= num; i++) {if (num % i == 0) return false;}return true;
}int main() {for (int i = 2; i <= 100; i++) {if (is_prime(i)) printf("%d ", i);}return 0;
}

9. 排序（冒泡、选择）

冒泡排序

void bubble_sort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}

选择排序

void selection_sort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {int min_index = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[min_index]) {min_index = j;}}int temp = arr[min_index];arr[min_index] = arr[i];arr[i] = temp;}
}

10. 查找（顺序、折半）

顺序查找

int sequential_search(int arr[], int n, int target) {for (int i = 0; i < n; i++) {if (arr[i] == target) return i;}return -1; // 未找到
}

折半查找（二分查找）

int binary_search(int arr[], int n, int target) {int left = 0, right = n - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) return mid;if (arr[mid] < target) left = mid + 1;else right = mid - 1;}return -1; // 未找到
}

（11）字符串处理

示例：字符串反转

#include <stdio.h>
#include <string.h>void reverse_string(char *str) {char *start = str;char *end = str + strlen(str) - 1;char temp;while (start < end) {temp = *start;*start++ = *end;*end-- = temp;}
}int main() {char str[] = "Hello, World!";reverse_string(str);printf("%s\n", str); // 输出: "!dlroW ,olleH"return 0;
}

（12）方程求根

示例：一元二次方程求根

#include <stdio.h>
#include <math.h>void quadratic_roots(double a, double b, double c, double *root1, double *root2) {double discriminant = b * b - 4 * a * c;if (discriminant > 0) {*root1 = (-b + sqrt(discriminant)) / (2 * a);*root2 = (-b - sqrt(discriminant)) / (2 * a);} else if (discriminant == 0) {*root1 = *root2 = -b / (2 * a);} else {printf("方程无实数根\n");*root1 = *root2 = 0; // 或者可以设置为 NAN}
}int main() {double a = 1, b = -3, c = 2;double root1, root2;quadratic_roots(a, b, c, &root1, &root2);if (root1 != root2) {printf("方程的两个根为 %.2f 和 %.2f\n", root1, root2);} else {printf("方程的重根为 %.2f\n", root1);}return 0;
}

（13）无穷级数求和

示例：求π的近似值（使用Gregory-Leibniz级数）

#include <stdio.h>double pi_approximation(int n) {double pi = 0.0;int sign = 1;for (int i = 0; i < n; i++) {pi += sign / (2.0 * i + 1.0);sign *= -1;}pi *= 4;return pi;
}int main() {int n = 1000000; // 增大n以获取更精确的π值printf("π的近似值为: %.15f\n", pi_approximation(n));return 0;
}

（14）其它算法

示例：大小写字母转换

#include <stdio.h>char to_upper(char c) {if (c >= 'a' && c <= 'z') {return c - 'a' + 'A';}return c; // 如果不是小写字母，则保持不变
}int main() {char c = 'b';printf("'%c' 的大写为: '%c'\n", c, to_upper(c)); // 输出: 'b' 的大写为: 'B'return 0;
}