复分析——第7章——ζ 函数和素数定理(E.M. Stein R. Shakarchi)

第7章 ζ函数和素数定理

Bernhard Riemann, whose extraordinary intuitive powers

we have already mentioned, has especially renovated

our knowledge of the distribution of prime numbers,

also one of the most mysterious questions in

mathematics. He has taught us to deduce results in

that line from considerations borrowed from the integral

calculus: more precisely, from the study of a

certain quantity, a function of a variable s which may

assume not only real, but also imaginary values. He

proved some important properties of that function,

but enunciated two or three as important ones without

giving the proof. At the death of Riemann, a note

was found among his papers, saying “These properties

of ζ(s) (the function in question) are deduced from an

expression of it which, however, I did not succeed in

simplifying enough to publish it.”

We still have not the slightest idea of what the

expression could be. As to the properties he simply

enunciated, some thirty years elapsed before I was able

to prove all of them but one. The question concerning

that last one remains unsolved as yet, though, by

an immense labor pursued throughout this last half

century, some highly interesting discoveries in that direction

have been achieved. It seems more and more

probable, but still not at all certain, that the “Riemann

hypothesis” is true.

( Bernhard Riemann，我们已经提到过，他非凡的直觉能力特别刷新了我们对素数分布的认识，素数分布也是数学中最神秘的问题之一。他教我们从积分学中借用的考虑因素那条线路来推导出结果：更准确地说，通过对某个量的研究，变量 s 的函数不仅可以假设实值，还可以假设虚值。他证明了该函数的一些重要性质，但在没有给出证明的情况下阐明了两三个重要性质。Riemann去世后，在他的论文中发现了一条注释，上面写着：“ζ(s)(问题中的函数)的这些性质是从它推导出来的表达式，然而，我并没有成功地简化到足以发布它的程度。”

我们仍然不知道这个表达是什么。至于他简单阐述的性质，大约三十年后我才能够证明除一个之外的所有性质。有关的问题尽管最后一个问题尚未解决，但通过过去半个世纪的巨大努力，在这方面已经取得了一些非常有趣的发现。“Riemann猜想”的正确性似乎越来越有可能，但仍不能确定。)

---------------------------------------------------------------------------J. Hadamard, 1945

Euler发现了(通过他的针对 ζ 函数的乘积公式)解析法和数(特别是素数)的算术属性之间的一种深层联系。Euler公式的一个容易导出的结果是，所有素数的倒数和 $\sum_{p}1/p$ 发散，这个结果量化了这个事实——存在无穷多个素数。然后，问题自然就变成了理解这些素数是如何分布的。带着这样的思考，我们考虑下面的函数：

π(x) = 小于或等于x的素数数量。

函数 π(x) 的不稳定(erratic)增长对于求得一个简单公式的希望渺茫。然而，我们被导向了研究 π(x) 随着 x 变得无穷大时的渐近(asymptotic)行为。在 Euler 的发现之后大约 60 年，Legendre 和 Gauss 在经过数次计算之后发现，很可能

(1) $\displaystyle {\pi}(x) \sim \frac{x}{\log{x}}$ (当 $x \longrightarrow \infty$ 时) 。

(当 x ⟶ ∞ 时，渐近关系 f (x) ~ g(x)意味着，当 x ⟶ ∞ 时，f (x)/ g(x) ~ 1 。) 另一个 60 年以后，在 Riemann 的工作之前不久，Tchebychev 通过初等方法(特别是，没有 ζ 函数 ) 更弱的结论

(2) $\displaystyle {\pi}(x) \approx \frac{x}{\log{x}}$ (当 $x \longrightarrow \infty$ 时) 。

在此，按照定义，符号“≈”意味着，存在正常量 A < B 使得

$\displaystyle A \frac{x}{\log{x}} \leq {\pi}(x) \leq B \frac{x}{\log{x}}$ (对于所有足够大的 x )。

在1896年，即Tchebychev结论之后大约40年，Hadamard和dela Vallée Poussin 给出了关系式(1)的有效证明。它们的这个结果被称为素数定理。这个定理的最初证明，以及我们下面给出的证明，使用复分析。我们应当注意到，由于随后发现了其它的证明方法，某些依赖复分析，而另外一些在特征上更为基础。

我们下面给出的素数定理证明的核心基于这个事实——ζ(s)在直线Re(s) = 1 上不会消没。事实上，我们可以证明，这两个命题是等价的。

1. ζ 函数的零点(Zeros of the zeta function)

我们在第1册第8章定理1.10中已经看到，Euler恒等式指出，对于Re(s) > 1 ，ζ函数可以被表示为一个无限积

$\displaystyle \zeta(s) = \prod_{p}^{}\frac{1}{1-p^{-s}}$ 。

为了完整起见，我们提供上述恒等式的证明。关键注意事项在于， $1/(1-p^{-s})$ 可以被写成一个收敛的(等比)幂级数

$\displaystyle 1 + \frac{1}{p^{s}} + \frac{1}{p^{2s}} + ... + \frac{1}{p^{Ms}} + ...$ ，

并在形式上取这些级数与所有素数 p 的乘积，产生了预期的结果。确切的论证按下述方式进行。

假设M 和N 是正整数且 M > N 。现在注意到，根据算术基本定理(注：第一卷第 8 章第一节给出了这一基本(但重要)事实的证明)。任意正整数 n ≤ N 可以被唯一地写成素数的一个乘式，并且出现在乘式中的每一个素数一定小于或等于N 并且重复小于M 次。因此，

$\begin{array}{rlc}\displaystyle \sum_{n=1}^{N} \frac{1}{n^{s}}&\displaystyle \leq \prod_{p \leq N}{\bigg (1 + \frac{1}{p^{s}} + \frac{1}{p^{2s}} + ...+ \frac{1}{p^{Ms}}} \bigg ) \\ \\ &\displaystyle \leq \prod_{p \leq N}\bigg (\frac{1}{1-p^{-s}} \bigg ) \\ \\ &\displaystyle \leq \prod_{p} \bigg ( \frac{1}{1-p^{-s}} \bigg ) \end{array}$ 。

现在，在级数中令 N 趋近于无穷大便产生

$\displaystyle \sum_{n=1}^{N}\frac{1}{n^{s}} \leq \prod_{p} \bigg ( \frac{1}{1-p^{-s}} \bigg )$ 。

对于反向的不等式，我们按如下论证。我们再次利用算术基本定理，求得

$\displaystyle \prod_{p \leq N}{\bigg (1 + \frac{1}{p^{s}} + \frac{1}{p^{2s}} + ...+ \frac{1}{p^{Ms}}} \bigg ) \leq \sum_{n=1}^{N} \frac{1}{n^{s}}$ 。

令 M 趋近于无穷大给到

$\displaystyle \prod_{p \leq N} \bigg ( \frac{1}{1-p^{-s}} \bigg ) \leq \sum_{n=1}^{N}\frac{1}{n^{s}}$ 。

因此，

$\displaystyle \prod_{p} \bigg ( \frac{1}{1-p^{-s}} \bigg ) \leq \sum_{n=1}^{N}\frac{1}{n^{s}}$ ，

从而ζ 乘积公式的证明完成。

从乘积公式我们看到(根据第5章命题3.1)，当 Re(s) > 1 时，ζ(s)不消没。

为了获得 ζ 的零点的位置的更进一步信息，我们使用提供给ζ解析延拓的函数方程。我们可以将基本关系式 ξ(s) = ξ(1 - s)写成下面的形式

$\displaystyle {\pi}^{-s/2}\Gamma(s/2)\zeta(s) = {\pi}^{-(1-s)/2}\Gamma{((1-s)/2)}\zeta(1-s)$ ，

因此，

$\displaystyle \zeta(s) = {\pi}^{s-1/2}\frac{\Gamma((1-s)/2)}{\Gamma(s/2)}\zeta(1-s)$ 。

现在，观察到，对于 Re(s) < 0 ,下列条款成立：

(i) ζ(1 - s)没有零点，因为 Re(1 - s) > 1 。

(ii) Γ((1-s)/2)是自由零的。

(iii) 1/Γ(s/2)在 s = -2，-4，-6，... 处具有零点。

因此，ζ 在Re(s) < 0 中的唯一零点位于负偶数 -2，-4，-6，... 处。

这证明了下面的定理。

定理 1.1 ζ 在带域 0 ≤ Re(s) ≤ 1 之外的唯一零点位于负偶数 -2，-4，-6，... 处。

有待研究的这个域称为临界带(critical strip)(0 ≤ Re(s) ≤ 1)。素数定理证明的关键事实在于ζ在直线 Re(s) = 1 上没有零点。作为这个事实和函数方程的一个简单的结论，可知 ζ 在直线 Re(s) = 0上没有零点。

在这篇创造性的(seminal)论文中，Riemann引入了ζ函数的解析延拓并证明了其函数方程，他将这些见解应用到素数理论中，并写下了确定素数分布的“明确(explicit)”公式。虽然他没有成功地充分证明和利用他的主张，但他确实提出了许多重要的新思想。他的分析使他深信后来被称为Riemann假设(Riemann hypothesis)的真理：

ζ(s)在临界域中的零点取决于直线 Re(s) = 1/2 。

对此他说道：“It would certainly be desirable to have a rigorous demonstration of this proposition; nevertheless I have for the moment set this aside, after several quick but unsuccessful attempts, because it seemed unneeded for the immediate goal of my study(对这个命题进行严格的论证当然是可取的；尽管如此，在几次快速但不成功的尝试之后，我暂时将其搁置一边，因为它对于我的研究的直接目标来说似乎不是必要的)。” 尽管许多理论和数值结果都表明该假设的有效性，但仍有待发现证明或反例。Riemann假设是当今数学中最著名的未解决问题之一。

特别是，正是出于这个原因，位于临界带之外的ζ的零点有时候也被称为 ζ 函数的平凡零点(trivial zeros)。此外，对于证明ζ 函数在实线段 0 ≤ σ ≤ 1 (其中，s = σ + it )没有零点的论证参见练习5。

在本节的余下部分，我们将局限于证明后续的定理，以及关于ζ 函数的相关估算，我们将用这些定理和估算证明素数定理。

定理 1.2 ζ 函数在直线 Re(s) = 1 上没有零点。

显然，因为我们知道，ζ在s = 1 处有一个极点，因此，在这个点的领域内不存在零点，但我们需要的是更深层的属性

ζ (1 + it ) ≠ 0 (对于任意 t∈ℝ ) 。

下列一系列引理汇聚了证明定理 1.2 的必要要素(ingredients)。

引理 1.3 若 Re(s) > 1 ，则

$\displaystyle \log{\zeta(s)} = \sum_{p,m}\frac{p^{-ms}}{m}= \sum_{n=1}^{\infty}c_{n} n^{-s}$ ( 对于某个 $c_{n} \geq 0$ )

证明：

假设 s > 1 。对Euler 乘积公式的对数，并使用对数的幂级数展式

$\displaystyle \log{ \bigg ( \frac{1}{1-x}\bigg ) } = \sum_{m=1}^{\infty}\frac{x^{m}}{m}$ ，

上式对于 0 ≤ x < 1 成立，我们求得

$\displaystyle \log{\zeta(s)} = \log{\prod}_{p}\frac{1}{1-p^{-s}} = \sum_{p}\log{\bigg ( \frac{1}{1-p^{-s}} \bigg ) } = \sum_{p,m}\frac{p^{-ms}}{m}$ 。

由于二重求和绝对收敛，因此我们不需要指定求和的顺序。参见本章末尾的评注。根据解释延拓，则这个公式对于所有的Re(s) > 1成立。注意，根据第3章定理6.2， $\log{\zeta}(s)$ 在简单连通的半平面 Re(s) > 1 中定义明确，因为 ζ 在这个半平面中没有零点。最后，很明显我们有

$\displaystyle \sum_{p,m}\frac{p^{-ms}}{m} = \sum_{n=1}^{\infty}c_{n}n^{-s}$ ，

其中，若 $n = p^{m}$ , 则 $c_{n} = 1/m$ ，而在其它情况下， $c_{n}=0$ 。

我们将给出的这个定理的证明取决于一个简单的技巧，这个技巧基于下列的不等式。

引理 1.4 若 θ ∈ ℝ ，则 $3 + 4\cos{(\theta)} + \cos{(2\theta)}\ge 0$ 。

从简单观察

$3 + 4\cos{(\theta)} + \cos{(2\theta)} = 2(1+\cos{(\theta)})^{2}$

立即就可推导出这个结论。

推论 1.5 若 σ > 1 且 t 是实数，则

$\log{\bigg | \zeta^{3} (\sigma)\zeta^{4} (\sigma+it)\zeta(\sigma+2it) \bigg | } \ge 0$ 。

证明：

令 $s = \sigma + it$ 并注意到

$\mathrm{Re}(n^{-s}) = \mathrm{Re}(e^{-(\sigma + it)\log{n}})= e^{-\sigma \log{n}}\cos(t\log{n} ) = n^{-\sigma}\cos{(t\log{n})}$ 。

因此，

$\begin{array}{l} \log \bigg |\zeta^{3}(\sigma)\zeta^{4} (\sigma+it)\zeta(\sigma+2it) \bigg | \\ \\ =3\log{|\zeta(\sigma)|}+4\log{|\zeta(\sigma+it)|}+\mathrm{\log{|\zeta(\sigma+2it)|}}\\ \\ =3\mathrm{Re}[\log{\zeta(\sigma)}]+4\mathrm{Re} [\log{\zeta(\sigma+it)}]+\mathrm{Re}[\log{\zeta(\sigma+2it)}] \\ \\ =\sum{c_{n}n^{-\sigma}}(3+4\cos{\theta_{n}}+\cos{2\theta_{n}}) \end{array}$ ，

其中， $\theta_{n}=t\log{n}$ 。现在，正值性(positivity)从引理1.4可推导，而事实上 $c_{n} \geq 0$ 。

现在，我们可以完成对定理的证明了。

定理1.2的证明：

假设相反情况成立，即 $\zeta(1+it_{0})=0$ ( 对于 $t_{0} \neq 0$ )。因为 ζ 在 $1+it_{0}$ 处是全纯的，它一定在这一点至少消没至1阶，因此，

$|\zeta(\sigma + it_{0}) |^{4} \leq C(\sigma-1)^{4}$ (当σ ⟶ 1 时，对于某个常量 C > 0)。

此外，我们知道，s = 1 是 ζ(s) 的一个简单极点，因此，

$|\zeta(\sigma ) |^{3} \leq C^{'} (\sigma-1)^{-3}$ ( 当σ ⟶ 1 时，对于某个常量 $C^{'}>0$ ) 。

最后，由于 ζ 在点 $\sigma + 2it_{0}$ 处是全纯函数，当 σ ⟶ 1 时，量 $|\zeta(\sigma + 2it_{0}) |$ 保持有界。将些事实结合在一起，便产生了

$|\zeta^{3} (\sigma)\zeta^{4} (\sigma+it)\zeta(\sigma+2it)| \longrightarrow 0$ (当 σ ⟶ 1 时) 。

这与推论1.5矛盾，因为位于0到1之间的实数的对数是负值。这就推断出了这个证明，即ζ 在实数直线 Re(s) = 1 上是自由零的。

1.1 对1/ζ(s)进行值算(Estimates for 1/ζ(s))

素数定理的证明取决于ζ 函数在直线 Re(s) = 1 附近的详细操控；涉及的基本对象是对数导数 $\zeta^{'}(s)/\zeta(s)$ 。出于这个原因，除了ζ在直线上的非消没，我们还需要知道关于 $\zeta^{'}$ 和 1/ζ(s) 的增长性。前者已按第6章命题2.7进行处理；现在我们处理后者。

随后的命题实际上是定理1.2的一个量化版本。

命题 1.6 对于每一个ε > 0 , 我们有 $1/|\zeta(s)| \leq c_{\epsilon} |t|^{\epsilon}$ (当 s = σ + it 且σ ≥ 1 和 |t| ≥ 1 时 )。

证明：

从我们前面的观察，很显然我们有

$\bigg |\zeta^{3} (\sigma)\zeta^4 (\sigma+it)\zeta(\sigma+2it) \bigg | \ge 1$ (只要σ ≥ 1 )。

使用第 6 章命题 2.7 的对 ζ 的估算，我们求得

$|\zeta^{4} (\sigma+it)| \ge c|\zeta^{-3} (\sigma)| |t|^{\epsilon} \ge c^{'}(\sigma-1)^{3}|t|^{-\epsilon}$ (对于任意σ ≥ 1 和 |t| ≥ 1)。

因此，

(3) $|\zeta(\sigma+it)| \ge c^{'}(\sigma-1)^{3/4}|t|^{-\epsilon/4}$ (只要σ ≥ 1 且 |t| ≥ 1)。

现在，我们考虑两种单独的情况，取决于，对于某个合适的常量A(其值我们后面再选择)，是否不等式 $\sigma - 1 \ge A|t|^{-5\epsilon}$ 成立。

若这个不等式确实成立，则(3)立即可得出

$\displaystyle |\zeta(\sigma+it)| \ge A^{'}|t|^{-4\epsilon}$ ，

在这种情况下，用 ε 替换掉 4ε 即可推导出预期的估算的证明。

然而，若 $\sigma - 1 < A|t|^{-5\epsilon}$ ，则首先选择 $\sigma^{'}>\sigma$ 且 $\sigma^{'}-1=A|t|^{-5\epsilon}$ 。则这个三角不等式意味着

$|\zeta(\sigma+it)| \ge |\zeta(\sigma^{'}+it)| - |\zeta(\sigma^{'}+it)-\zeta(\sigma+it)|$ ，

并应用中值定理，以及结合前一章所获得的ζ 的导数估算，给出

$|\zeta(\sigma^{'}+it)-\zeta(\sigma+it)| \leq c^{''} |\sigma^{'}-\sigma||t|^{\epsilon} \leq c^{''} |\sigma^{'}-1||t|^{\epsilon}$ 。

这些观察结果，再结合(3)的应用(其中，我们令 $\sigma^{'}=\sigma$ )，可证明

$|\zeta(\sigma+it)| \ge c^{'}(\sigma^{'}-1)^{3/4} |t|^{-{\epsilon}/4} - c^{''}|\sigma^{'}-1||t|^{\epsilon}$ 。

现在，选择 $A = (c^{'}/(2c^{''}))^{4}$ ，并回顾 $\sigma^{'} - 1 = A|t|^{-5\epsilon}$ 。这恰好给出

$c^{'}(\sigma^{'}-1)^{3/4} |t|^{-{\epsilon}/4}=2c^{''}(\sigma^{'}-1)|t|^{\epsilon}$ ，

因此，

$|\zeta(\sigma+it)| \ge A^{''}|t|^{-4\epsilon}$ 。

在用ε 替换掉 4ε 之后，就建立了预期的不等式，则命题的证明完成。

2. 函数 𝜓 和 𝜓1(x) 的简化(Reduction to the functions 𝜓 and 𝜓1(x) )

Tchebychev在他的素数研究的过程中，引入了一个辅助函数，此函数的行为在很大程度上等价于素数的渐近分布，但又比π(x)更容易操控。Tchebychev的 𝜓 函数被定义为

$\displaystyle \psi(x) = \sum_{p^{m} \leq x}\log{p}$ 。

即对那些小于或等于 x 的形如 $p^{m}$ 的整数求和。此处 p是一个素数而 m是一个正整数。还有另外两种我们将要用到的 𝜓 函数的其它格式。首先，若我们定义

则很显然

$\displaystyle \psi(x) = \sum_{1 \leq n \leq x}\Lambda(n)$ 。

此外，立即可得出

$\displaystyle \psi(x) = \sum_{p \leq x}\bigg [ \frac{\log{x}}{\log{p}} \bigg ] \log{p}$ 。

其中，[u ] 表示 ≤ u 的最大整数，和式是对小于或等于x 的素数求和。若 $p^{m} \leq x$ ，则 $m \leq \log{x}/\log{p}$ ，可以从这个事实推导出这个公式。

𝜓(x)包含关于π(x)的足够信息来证明我们的定理，这个事实将在下一命题的表述中被赋予准确的意义。特别是，这将素数定理简化为有关 𝜓 的相应渐近表述。

命题 2.1 若当 x ⟶ ∞ 时， 𝜓(x) ~ x ，则当 x ⟶ ∞ 时， $\pi(x) \sim x/\log{x}$ 。

证明：

此处的论证是初等的。根据定义，只需证明以下两个不等式即可：

(4) $\displaystyle 1 \leq \lim_{x \rightarrow \infty}{\inf{{\pi}(x)\frac{\log{x}}{x}}}$ 和 $\displaystyle \lim_{x \rightarrow \infty}{\sup{{\pi}(x)\frac{\log{x}}{x}}} \leq 1$ 。

为此，首先注意到，大致的估算给出

$\displaystyle \psi(x) = \sum_{p \leq x}\bigg [ \frac{\log{x}}{\log{p}} \bigg ] \log{p} \leq \sum_{p \leq x}\frac{\log{x}}{\log{p}}\log{p}=\pi{(x)}\log{x}$ 。

再通过除以 x 而得到

$\displaystyle \frac{\psi(x)}{x} \leq \frac{\pi{(x)}\log{x}}{x}$ 。

因此，

$\psi(x) + \alpha{\pi}(x^{\alpha})\log{x} \ge \alpha {\pi}(x)\log{x}$ 。

除以 x，注意到， $\pi(x^{\alpha}) \leq x^{\alpha}$ ，α < 1 ，并且 𝜓(x) ~ x ，给出

$\displaystyle 1 \ge \alpha \lim_{x \rightarrow \infty}{\sup{{\pi}(x)\frac{\log{x}}{x}}}$ 。

由于α < 1 是任意的，因此证明完成。

评注：

命题的逆向也成立： $\pi(x) \sim x/\log{x}$ 则 𝜓(x) ~ x 。由于我们不需要这个结论，因此，我们将其证明留给感兴趣的读者去完成。

事实上，使用 𝜓 函数的近亲(cousin)会更方便。定义函数 $\psi_{1}$ 为

$\displaystyle \psi_1(x) = \int_{1}^{x}\psi(u)du$ 。

在前面的素数定理中，我们将素数定理简化为当 x 趋近于无穷大时𝜓(x)的渐近函数。接下来，我们将证明，可以从 $\psi_{1}$ 的渐近性推导出这个渐近函数。

命题 2.2 若当 x ⟶ ∞ 时， $\psi_{1}(x) \sim x^{2}/2$ ，则当 x ⟶ ∞ 时，𝜓(x) ~ x ，且因此有当 x ⟶ ∞ 时， $\psi(x) \sim x/\log{x}$ 。

证明：

根据命题2.1 ，只需证明当 x ⟶ ∞ 时，𝜓(x) ~ x 即可。从以下事实，相当容易推导出，即，若 α < 1 < β ，则

$\displaystyle \frac{1}{(1-\alpha)x} \int_{{\alpha}x}^{x}\psi(u)du \leq \psi(x) \leq \frac{1}{(\beta-1)x} \int_{x}^{{\beta}x}\psi(u)du$ 。

这个二重不等式的证明是直接的，并且简单地取决于 𝜓 是递增的事实。因此，我们求得(例如)

$\displaystyle \psi(x) \leq \frac{1}{(\beta-1)x}\bigg [\psi_{1} ({\beta}x)-\psi_{1} (x) \bigg ]$ ，

因此，

$\displaystyle \frac{\psi(x)}{x}\leq \frac{1}{(\beta-1)}\bigg [\frac{\psi_{1} ({\beta}x)}{({\beta}x)^{2}}\beta^{2} -\frac{\psi_{1} (x)}{x^{2}} \bigg ]$ 。

继而，这又意味着

$\displaystyle \lim_{x \rightarrow \infty}{\sup_{}{\frac{\psi(x)}{x}}} \leq \frac{1}{(\beta-1)}\bigg [\frac{1}{2}\beta^{2}-\frac{1}{2}\bigg ] = \frac{1}{2}(\beta + 1)$ 。

由于这个结论对于所有 β > 1 都成立，因此，我们已经证明了 $\lim_{x \rightarrow \infty}{\sup_{}{\frac{\psi(x)}{x}}} \leq 1$ 。α < 1 也具有类似的论证，则证明了 $\lim_{x \rightarrow \infty}{\inf_{}{\frac{\psi(x)}{x}}} \ge 1$ ，因此，命题的证明完成。

现在到了该把 $\psi_{1}$ (因此，就还有 𝜓 )与ζ 关联起来的时候了。我们在引理1.3中证明了对于 Re(s) > 1 ，有

$\displaystyle \log{\zeta(s)} = \sum_{m,p}\frac{p^{-ms}}{m}$ 。

微分这个表达式得到

$\displaystyle \frac{\zeta^{'}(s)}{\zeta(s)}= -\sum_{m,p}(\log{P})p^{-ms} = -\sum_{n=1}^{\infty}\frac{\Lambda(n)}{n^{s}}$ 。

我们将对于 Re(s) > 1 时的这个公式记为

(5) $\displaystyle -\frac{\zeta^{'}(s)}{\zeta(s)}=\sum_{n=1}^{\infty}\frac{\Lambda(n)}{n^{s}}$ 。

渐近行为 $\psi_{1}(x) \sim x^{2}/2$ 将是将是通过 $\psi_{1}$ 和 ζ 之间关系的(5)得出的结果，这种关系通过下面的显著的积分公式加以描述。

命题 2.3 对于所有的 c > 1

(6) $\displaystyle \psi_{1}(x)=\frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}\frac{x^{s+1}}{s(s+1)}\bigg ( -\frac{\zeta^{'}(s)}{\zeta(s)} \bigg)ds$ 。

为了使得这个公式的证明清晰，我们在一个引理中分离出必要的周线积分。

引理 2.4 若 c > 0，则

$\displaystyle \frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}\frac{a^{s}}{s(s+1)}ds=\left \{ \begin{array}{lrc} 0(if \:\:0 < a \leq 1) \\ \\ 1-\frac{1}{a}(if \:\: 1 \leq a) \end{array} \right.$ 。

此处，积分是在垂线 Re(s) = c 上进行的。

证明：

首先注意到，由于 $|a^{s}| = a^{c}$ ，积分收敛。我们首先假设 1 ≤ a ，并写成 $a=e^{\beta}$ 且 $\beta = \log{a} \ge 0$ 。令

$\displaystyle f(s)=\frac{a^{s}}{s(s+1)}=\frac{e^{s\beta}}{s(s+1)}$ 。

则 $res_{s=0}{f}=1$ 和 $res_{s=-1}{f}=-1/a$ 。对于 T > 0 ，考虑图1所示的路径 Γ(T ) 。

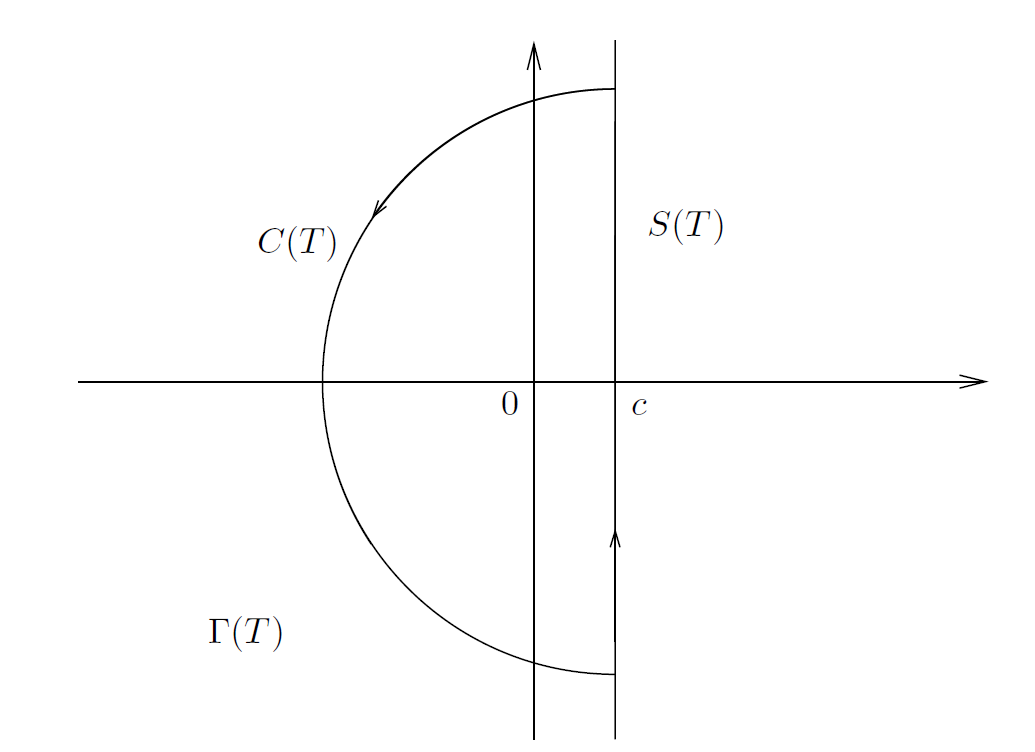
----------------------------------图1: 引理2.4的证明中用到的当 a ≥ 1时的周线--------------------------------

积分路径Γ(T )由从 c – iT 到 c + iT 的线段和圆心位于c半径为T的位于垂线段的左边的半圆构成。我们为Γ(T ) 配备正(逆时针)方向，并注意我们正在处理可构周线(toy contour)。如果我们选择足够大的 T 使得 0 和 −1 包含在Γ(T ) 的内部，则根据留数公式

$\displaystyle \frac{1}{2{\pi}i}\int_{\Gamma(T)}f(s)ds = 1 - \frac{1}{a}$ 。

由于

$\displaystyle \frac{1}{2{\pi}i}\int_{\Gamma(T)}f(s)ds = \frac{1}{2{\pi}i}\int_{S(T)}f(s)ds + \frac{1}{2{\pi}i}\int_{C(T)}f(s)ds$ ，

只需证明半圆上的积分随着 T 趋近于无穷大而趋近于 0 。注意，若 s = σ + it∈C(T ) ，则对于任意大的T 我们有

$| s(s + 1)| \ge (1/2)T^{2}$ ，

并由于 σ ≤ c 我们还有估算 $|e^{{\beta}s}| \leq e^{{\beta}c}$ 。因此，

$\displaystyle \bigg | \int_{C(T)}f(s)ds \bigg | \leq \frac{C}{T^{2}}2{\pi}T \rightarrow 0$ (当 T ⟶ ∞ 时) 。

因此，当 a ≥ 1 时的这种情况得证。

若 0 < a ≤ 1 ，考虑一个类似的周线，但是这次这个半圆位于直线 Re(s) = c 的右侧。注意到，在这个周线内部没有极点，我们可以给出类似于上面给出的类似证明，以证明当 T 趋近于无穷大时这个半圆上的积分趋近于0。

现在，我们准备证明命题2.3 。首先，注意到

$\displaystyle \psi(u) = \sum_{n=0}^{\infty}\Lambda(n)f_{n} (u)$ ，

其中，若 n ≤ u 则 $f_{n} (u)=1$ ，而若在其它情况下则 $f_{n} (u)=0$ 。因此，

$\begin{array}{rlc} \psi_{1}(x) &\displaystyle=\int_{0}^{x}\Psi(u)du \\ \\ &\displaystyle=\sum_{n=1}^{\infty}\int_{0}^{x}{\Lambda}f_{n}(u)du \\ \\ &\displaystyle=\sum_{n \leq x}\Lambda(n)\int_{n}^{x}du \end{array}$ ，

继而，

$\displaystyle \psi_{1}(x) =\sum_{n \leq x}\Lambda(n)(x-n)$ ，

这个事实，连同等式(5)以及引理2.4的应用一起(具有 a = x/n)，给出

$\begin{array}{rlc} \displaystyle \frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}\frac{x^{s+1}}{s(s+1)}\bigg ( -\frac{\zeta^{'}(s)}{\zeta(s)} \bigg)ds &\displaystyle=x\sum_{n=1}^{\infty}{\Lambda}(n)\frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}\frac{(x/n)^{s}}{s(s+1)}ds \\ \\ &\displaystyle=x\sum_{n \leq x}\Lambda(n)\left (1-\frac{x}{n} \right ) \\ \\ &\displaystyle=\psi_{1}(x) \end{array}$ ，

正如所要证的那样。

2.1 对 𝜓1(x) 渐近性的证明(Proof of the asymptotics for 𝜓1(x) )

在这一节，我们将证明

$\psi_{1}(x) \sim x^{2}/2$ ( 当 x ⟶∞ 时) ，

最终，我们将会完成对素数定理的证明。

论证过程中的关键材料(ingredients)是：

$\bullet$ 命题 2.3 中联系 $\psi_{1}$ 与ζ 的公式，即

$\displaystyle \psi_{1}(x)=\frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}\frac{x^{s+1}}{s(s+1)}\bigg ( -\frac{\zeta^{'}(s)}{\zeta(s)} \bigg)ds$ (对于 c > 1 ) 。

$\bullet$ ζ 函数在 Re(s) = 1 上的非消没性，即

ζ(1 + it) ≠ 0 (对于任意 t∈ ℝ) ，

以及第 6 章命题 2.7 和本章命题 1.6 中给出的直线附近的ζ 的估计值。

现在我们更详细地讨论我们的策略。在上述 $\psi_{1}(x)$ 的积分中，我们想改变积分线 Re(s) = c (c > 1)为 Re(s) = 1 。若我们可以实现，被积函数中的因子 $x^{s+1}$ 的大小则会是阶 $x^{2}$ (这已接近我们的预期)，而不是 Re(s) = c (c > 1)(这个值太过庞大)。然而，还有两个售点问题必须处理。第一个问题是ζ(s)函数在 s = 1 处的极点；事实证明，当考虑这个极点的时候，其贡献恰好是 $\psi_{1}(x)$ 的渐近的主要项 $x^{2}/2$ 。第二，余下必须证明的是，在本质上小于该项，因此，当在直线 Re(s) = 1 上进行积分时，我们必须进一步完善阶 $x^{2}$ 的粗略估算。我们按如下方式执行我们的计划。

固定 c > 1 (比如，c = 2)，并假设这时 x 也是固定的且 x ≥ 2 。令 F(s) 表示被积函数

$\displaystyle F(s)=\frac{x^{s+1}}{s(s+1)}\bigg ( -\frac{\zeta^{'}(s)}{\zeta(s)} \bigg)$ 。

首先，我们将从 c - i∞ 到 c + i∞ 的垂线变形为如图2所示的路径 γ(T )。(在直线 Re(s) = 1 上的 γ(T ) 的线段由 T ≤ t < ∞ 和 -∞ < t ≤ -T 构成。) 在此 T ≥ 3 ，而此后T 的值将选作一个合适的更大值。

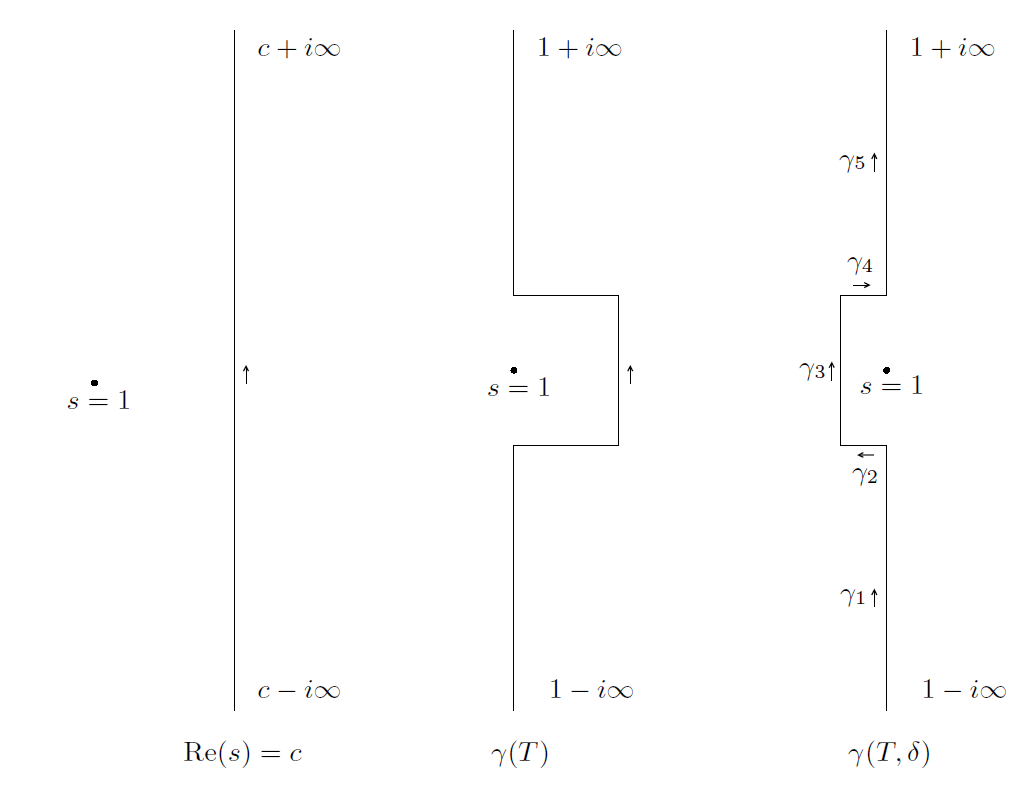
---------------------------------图2：三段线：垂线 Re(s) = c ，周线 γ(T )和 γ(T，δ)--------------------------

常见而熟悉的使用Cauchy定理的论证让我们看到

(7) $\displaystyle \frac{1}{2{\pi}i}\int_{c-i\infty}^{c+i\infty}F(s)ds=\frac{1}{2{\pi}i}\int_{\gamma(T)}^{}F(s)ds$ 。

事实上，基于第6章命题2.7和命题1.6，我们知道，对于任意固定的 η> 0 ,只要 s = σ + it (σ ≥ 1 且 |t| ≥ 1 ), 就有 $|\zeta^{'}(s)/\zeta(s)| \leq A|t|^{\eta}$ 。因此， $|F(s)| \leq A^{'}|t|^{-2+\eta}$ 在两个(无限)矩形中以直线 (c - i∞ , c + i∞)和γ(T )为界。由于 F 在那个区域中是规整的，其在无穷远处的递降足够迅速，因此论断(7)成立。

接下来，我们从周线γ(T )过度到周线 γ(T，δ )。(再次见图2。) 为了固定T，我们选取δ > 0 足够小，以使得 ζ 在那个格子

$\{ s = \sigma + it ,1-\sigma \leq \sigma \leq 1 , |t|\leq T \}$

中没有零点。可以作出这样一个选择，因为 ζ在直线σ = 1 上不消没。

现在，F(s) 在 s = 1 处有一个简单极点。事实上，根据第6章中的推论2.6 ，我们知道 ζ(s) = 1/( s - 1) + H(s) (其中， H(s)在s = 1附近是规整的)。因此， $-\zeta^{'} (s)/\zeta(s) = 1/( s - 1) + h(s)$ (其中， h(s)在s = 1附近是全纯的)，因此，F(s)在s = 1附近的留数等于 $x^{2}/2$ 。最终，

$\displaystyle \frac{1}{2{\pi}i}\int_{\gamma(T)}^{}F(s)ds=\frac{x^{2}}{2}+\frac{1}{2{\pi}i}\int_{\gamma(T,\delta)}^{}\frac{x^{s+1}}{s(s+1)}F(s)ds$ 。

现在，我们将周线 γ(T，δ) 分解为 $\gamma_{1} + \gamma_{2} + \gamma_{3} + \gamma_{4} + \gamma_{5}$ 和每一个积分 $\int_{\gamma_{j}}F(s)ds$ ( j = 1, 2, 3, 4, 5 且 $\gamma_{j}$ 如图2所示)的估算。

首先，我们断言，存在这么大的T 使得

$|\int_{\gamma_{1}}F(s)ds|\leq \frac{\epsilon}{2}x^{2}$ 和 $|\int_{\gamma_{5}}F(s)ds|\leq \frac{\epsilon}{2}x^{2}$ 。

为了理解这一点，我们首先注意到，对于 $s \in \gamma_{1}$ ，我们有

$|x^{1+s}| = x^{1+\sigma} = x^{2}$ 。

则，根据命题1.6，我们有(例如)， $|\zeta^{'}(s)/\zeta(s)| \leq A|t|^{1/2}$ ，因此，

$\displaystyle \bigg|\int_{\gamma_{1}}F(s)ds \bigg |\leq Cx^{2}\int_{T}^{\infty}\frac{|t|^{1/2}}{t^{2}}dt$ 。

由于这个积分收敛，我们可以取T足够大从而使得右边 ≤ ${\epsilon}x^{2}/2$ 。在 $\gamma_{5}$ 上的积分的论证相同。

已经固定了T之后，我们选择恰当小的δ 。注意到，在 $\gamma_{3}$ 上，有

$|x^{1+s}| = x^{1+1-\sigma} = x^{2-\sigma}$ ，

据此，我们推导出存在一个常量 $C_{T}$ (取决于T )使得

$\displaystyle \bigg|\int_{\gamma_{3}}F(s)ds \bigg |\leq C_{T}x^{2-\delta}$ 。

最后，在小的水平线段 $\gamma_{2}$ 上(以及类似地，在 $\gamma_{4}$ 上)，我们可以如下估算积分：

$\displaystyle \bigg|\int_{\gamma_{2}}F(s)ds \bigg |\leq C_{T}^{'}\int_{1-\delta}^{1}x^{1+\sigma}d\sigma\leq C_{T}^{'}\frac{x^{2}}{\log{x}}$ 。

我们推断出，存在常量 $C_{T}$ 和 $C_{T}^{'}$ (可能有别于前述常量)使得

$\displaystyle \bigg|{\psi}_{1}(x)-\frac{x^{2}}{2} \bigg |\leq {\epsilon}x^{2}+ C_{T}x^{2-\delta} +C_{T}^{'}\frac{x^{2}}{\log{x}}$ 。

通过除以 $x^{2}/2$ ，我们发现

$\displaystyle \bigg|\frac{2{\psi}_{1}(x)}{x^{2}}-1\bigg |\leq 2{\epsilon}+2 C_{T}x^{-\delta} +2C_{T}^{'}\frac{1}{\log{x}}$ ，

因此，对于任意大的 x，我们有

$\displaystyle \bigg|\frac{2{\psi}_{1}(x)}{x^{2}}-1\bigg | \leq 4\epsilon$ 。

这就推导出了证明

$\psi_{1}(x) \sim x^{2}/2$ ( 当 x ⟶∞ 时),

因此，我们已经完成了素数定理的证明。

关于双重求和交换的注意事项

我们证明下列关于无穷和交换的事实：若 $\{a_{k\ell}\}_{1{\leq}k,{\ell}<\infty }$ 是一个下标索引为 ℕ × ℕ 的复数序列，并使得

(8) $\displaystyle \sum_{k=1}^{\infty}\bigg (\sum_{\ell=1}^{\infty}|a_{k}{\ell} | \bigg ) < \infty$ ，

则：

(i) 按这种次序求和的双重和 $A= \sum_{k=1}^{\infty}\bigg (\sum_{\ell=1}^{\infty}|a_{k}{\ell} | \bigg )$ 收敛，而事实上，我们也可以交换求和次序，因此

$A= \sum_{k=1}^{\infty}\sum_{\ell=1}^{\infty}a_{k\ell}= \sum_{\ell=1}^{\infty}\sum_{k=1}^{\infty}a_{k\ell}$ 。

(ii) 已知 ε > 0 ,存在一个正整数N，使得对于任意 K,L > N ，我们有

$|A-\sum_{k=1}^{K}\sum_{\ell=1}^{L}a_{k\ell}|<\epsilon$ 。

(iii) 若 m ⟼ (k(m), 𝓁(m))是一个从 ℕ 到 ℕ × ℕ 的双射，若我们写成 $c_{m} = a_{k(m)\ell(m)}$ ，则 $A = \sum_{k=1}^{\infty}c_{k}$ 。

表述(iii)指的是，序列 $\{a_{k\ell} \}$ 的次序的任何重排不影响求和极限。这可类比于级数绝对收敛的情况(可按任意期望次序求和)。

条件(8)指的是，每一个和式 $\sum_{\ell}a_{k\ell}$ 绝对收敛，此外，这个收敛是按k“一致的”。函数序列也会出现类似的情况，其中，一个重要的问题是，是否极限的交换

$\displaystyle \lim_{x{\rightarrow}x_{0}}\lim_{n{\rightarrow}\infty}{f_{n}(x)} \overset{?}{=} \lim_{n{\rightarrow}\infty}\lim_{x{\rightarrow}x_{0}}{f_{n}(x)}$

成立。一个众所周知的事实是，若系列 $f_{n}$ 是连续的，并且它们一致收敛，则以上恒等式成立，因为极限函数其自身是连续的。为了利用这一事实，定义 $b_{k}=\sum_{\ell=1}^{\infty}|a_{k\ell}|$ 并令 $S = \{ x_{0} , x_{1} ,...\}$ 为一个可数点集且 $\displaystyle \lim_{n {\rightarrow} \infty}{x_{n}}=x_{0}$ 。此外，在 S 上定义系列函数如下

$\displaystyle f_{k} (x_{0}) = \sum_{\ell=1}^{\infty}a_{k{\ell}}$ (对于 k = 1, 2 , ...)

$\displaystyle f_{k} (x_{n}) = \sum_{\ell=1}^{n}a_{k{\ell}}$ (对于 k = 1, 2 , ...和 n = 1, 2 , ...)

$\displaystyle g(x)=\sum_{k=1}^{\infty}f_{k}(x)$ (对于 x∈S ) 。

按照假设(8) ,每一个 $f_{k}$ 在 $x_{0}$ 点都是连续的。此外， $|f_{k}(x)| \leq b_{k}$ 且 $\sum{b_{k}} < \infty$ ，因此，定义函数 g的序列在S 上是一致收敛的，因此，g 在 $x_{0}$ 点也是连续的。最终，我们求得(i),因为，

$\begin{array}{rlc}\displaystyle \sum_{k=1}^{\infty}\sum_{\ell=1}^{\infty}a_{k\ell}&\displaystyle=g(x_{0})=\lim_{n \rightarrow \infty}g(x_{n})=\lim_{n \rightarrow \infty}\sum_{k=1}^{\infty}\sum_{\ell=1}^{n}a_{k\ell} \\ \\ &\displaystyle=\lim_{n \rightarrow \infty}\sum_{\ell=1}^{n}\sum_{k=1}^{\infty}a_{k\ell}=\sum_{\ell=1}^{\infty}\sum_{k=1}^{\infty}a_{k\ell} \end{array}$ 。

对于第二个表述，首先注意到

$\displaystyle \left |A- \sum_{k=1}^{K}\sum_{\ell=1}^{L}a_{k\ell} \right | \leq \sum_{k \leq K}\sum_{\ell>L}\bigg |a_{k\ell} \bigg | + \sum_{k>K}\sum_{\ell=1}^{\infty}\bigg |a_{k\ell} \bigg |$ 。

为了估算第二项，我们使用 $\sum{b_{k}}$ 收敛的事实，这意味着 $\sum_{k>K}\sum_{\ell=1}^{\infty}|a_{k\ell}|< \epsilon/2$ (对于某个 $K_{0}$ ，只要 $K>K_{0}$ )。对于上述第一项，注意到 $\sum_{k \leq K}\sum_{\ell>L} |a_{k\ell} | \leq \sum_{k=1}^{\infty}\sum_{\ell>L} |a_{k\ell} |$ 。但上述论证确保了我们可以交换最后两个和；此外， $\sum_{\ell=1}^{\infty}\sum_{k=1}^{\infty}|a_{k\ell}|<\infty$ ，因此，对于任意 $L>L_{0}$ ，我们有 $\sum_{\ell>L}^{}\sum_{k=1}^{\infty}|a_{k\ell}|<\epsilon/2$ 。取 $N > \max(L_{0}, K_{0})$ 就完成了对(ii)的证明。